核心思想

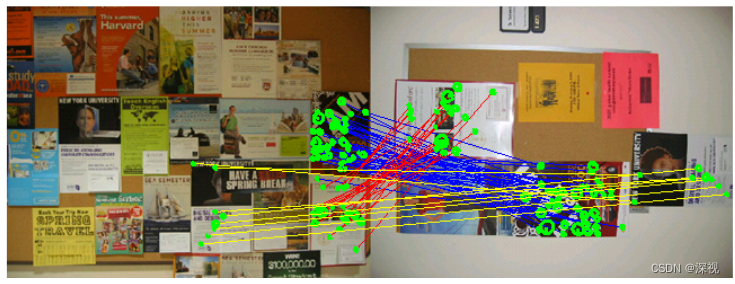
  两组点集中共有的匹配区域通常具备两个特点：1.局部的特征相似；2.特征点在空间上的分布也相似。作者将候选匹配点对作为图的节点，将两种相似性统一到边的权重来表示。通过寻找图中稠密连接的子图来寻找两个点集中的匹配区域，如下图所示

实现过程

  首先，利用SIFT等算法分别从两幅图像中提取特征点集$P,Q$，其中的特征点$p$包含两个特征信息$p_d,p_c$，$p_d$表示由SIFT提取的局部特征向量，$p_c$表示特征点的坐标。内积空间$C=P\times Q$表示所有可能的对应关系，每组对应点$c_i$都由一对点$(i,i^{\prime })$表示，其中$i\in P,i^{\prime }\in Q$。每组对应点的局部特征相似得分$S_{c_i}=f_1(i_d,i_d^{\prime })$，由于匹配点通常局部特征都比较相似，因此仅保留相似得分较大的对应点 M = { c ∣ c ∈ C , S c > ϵ } M=\{c|c\in C, S_{c}>\epsilon \} M={c∣c∈C,Sc​>ϵ}。

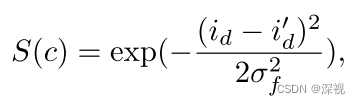
  对于两组对应点$c_i=(i,i^{\prime })$和$c_j=(j,j^{\prime })$，设第一幅图中的点$i$和$j$之间的距离为$l_{ij}$，第二幅图中的点$i^{\prime }$和$j^{\prime }$之间的距离为$l_{i^{\prime }{j}^{\prime }}$。如果它们是两组匹配点，那么我们应该可以通过对第二幅图放缩$l_{ij}/l_{i^{\prime }{j}^{\prime }}$倍，来使两组点对齐。同理，如果两个公共的匹配区域包含$n$组对应点，那么他们两两之间构成的匹配关系应该有较为接近的放缩系数，而噪点或离群点通常不具备这样的特点。两组对应点之间的几何一致性得分$S_{c_i{c}_j}(s)=f_2(|l_{ij}-s{l}_{i^{\prime }{j}^{\prime }}|)$，$s$表示放缩系数。$f_2(x)$是一个非负单调递减函数，本文中取

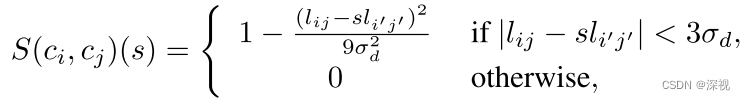
  假设一个对应点集$M$包含$m$组对应点， M = { c 1 , c 2 . . . c m } M=\{c_1, c_2...c_m\} M={c1​,c2​...cm​}。可以构建一个包含$m$个节点的图$G$，每个节点都表示一组对应点，这个图称之为动态对应图（dynamic correspondence graph）。节点$i$和$j$之间的边的权重$w_{ij}$可表示为

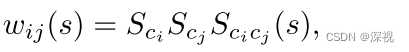
该权重与放缩系数$s$有关，则加权邻接矩阵$A(s)$可定义为

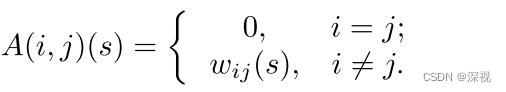
$A(s)$是一个对称的非负矩阵。
  对于一个由$n$个特征点构成的共同匹配区域，当选择正确的放缩系数$s_0$时，对应点之间的局部特征相似得分和几何一致性得分应该都很高，即边的权重会较大，那么就对应图$G$中的一个稠密子图$T$。这个稠密子图具备较高的平均类内相似性得分（average intra-cluster affinity score）$S_{av}(s_0)=\frac{1}{n^2}{\sum }_{i\in T,j\in T}A(i,j)(s_0)$。如果使用指示向量$y$来表示$T$，即如果$i\in T$，$y(i)=1$否则为$0$。则$S_{av}(s_0)$可表示为$S_{av}(s_0)=\frac{1}{n^2}{y}^{T}A(s_0)y=x^{T}A(s_0)x$，其中$x=y/n$。由于${\sum }_{i}y(i)=n$，则${\sum }_{i}x(i)=1$。
  根据Motzkin-Straus定理，下式中的局部极大值点就对应图中的一个最大团

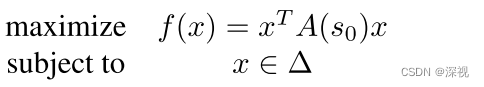
其中

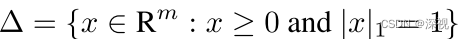
简而言之，作者将寻找图$G$中稠密子图$T$的问题转化为了求解目标函数$f(x)$的局部极大值点的问题。
  给定一个放缩系数$s_0$，优化目标函数$f(x)$可能包含许多的局部极大值点，极值点的值越大越有可能对应正确的公共匹配区域。给定一个初始的$x(1)$，则$f(x)$的局部极大值点$x^{\ast }$可通过模仿者等式 （Replicator Equation）得到

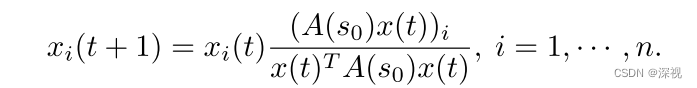
通过迭代计算上述等式，当数值收敛于稳定点时，则对应于$f(x)$的一个局部极大值点。
  为了找到全部的局部最大值点 { x ∗ } \{x^*\} {x∗}，可以提供多个初始化$x(1)$分别进行迭代计算。由于局部最大值点$x^{\ast }$对应于共同匹配区域，因此它具备两个特性：

1. 局部性，对于图$G$中每个节点$v$，包含$v$在内的共同匹配区域是$N(v)\cup v$的子集，$N(v)$表示$v$的邻域。因此只需要对图$G$中每个节点$v$的邻域中对$x(1)$进行初始化。
2. 非交叉性，两个不同的共同匹配区域通常不会包含公共的顶点。这意味这两个局部极大值点$x^{\ast },y^{\ast }$，其对应两个不同的共同匹配区域，应满足$x^{\ast T}{y}^{\ast }\approx 0$。

  利用上述特性，可以对图$G$中的每个节点及其邻域分别进行初始化，然后通过模仿者等式寻找到该初始化对应的局部极大值点。将所有的局部极大值点进行降序排列，并将极值较小的点舍去。最后，根据$x^{\ast T}{y}^{\ast }$是否大于$\eta$来将局部极大值点进行合并，从而求得最终要保留的局部极大值点，如算法1所示

  得到局部极大值点还要将其恢复到对应的共同匹配区域，$x^{\ast }$中的每个点$x_i^{\ast }$表示对应点$i$是正确匹配点的概率，可以通过算法2得到共同匹配区域

  在实际应用中，放缩系数$s$通常属于一个范围$R=[s_0,s_1]$，因此可以通过在该范围内均匀采样得到$s$，然后分别计算不同放缩系数条件下对应的共同匹配区域，如算法3所示

创新点

• 将特征点的匹配问题转化为了寻找图的最大团问题
• 利用共同匹配区域的局部性和非交叉性来优化求解过程

算法总结

  作者关注的是寻找两幅图中局部的共同匹配区域问题，并且非常巧妙地将其转化为了寻找图的最大团问题，并利用了共同匹配区域的局部性和非交叉性来优化求解过程，使其能够更好更快地求解。该方法还有一个优势是可以解决一对一、一对多和多对多的匹配问题，这在应用中具备很高的价值。