Xgboost 方式一

from xgboost import XGBClassifier
model = XGBClassifier(
    learning_rate =0.1, # 学习率，控制每次迭代更新权重时的步长，默认0.3。值越小，训练越慢
    use_label_encoder=False,
    n_estimators=10,   # 总共迭代的次数，即决策树的个数
    max_depth=5,       # 深度
    min_child_weight=1,  # 默认值为1,。值越大，越容易欠拟合；值越小，越容易过拟合
    gamma=0,        # 惩罚项系数，指定节点分裂所需的最小损失函数下降值。
    # 训练每棵树时，使用的数据占全部训练集的比例。默认值为1，典型值为0.5-1。防止overfitting
    subsample=0.8,  
    colsample_bytree=0.8,
    objective= 'binary:logistic',  # 目标函数
    eval_metric = ['merror'],  # 验证数据集评判标准
    nthread=4,)    # 并行线程数
eval_set = [(X_test, y_test),(X_train,y_train)]
model.fit(X_train,y_train,eval_set = eval_set,verbose = True)

Xgboost 方式二

import xgboost as xgb
param = {'learning_rate':0.1, 'n_estimators':10,
         'max_depth':5,'min_child_weight':1,'gamma':0,'subsample':0.8,
         'colsample_bytree':0.8, 'verbosity':0,'objective':'multi:softprob'}
model = xgb.XGBClassifier(**param)
model.fit(X_train, y_train, early_stopping_rounds=20, eval_metric='merror',
        eval_set=[(X_test, y_test)])

Xgboost 方式三

import xgboost as xgb
dtrain = xgb.DMatrix(data = X_train,label = y_train)
dtest = xgb.DMatrix(data = X_test,label = y_test)
param = {'learning_rate':0.1,'use_label_encoder':False,'n_estimators':20,
         'max_depth':5,'min_child_weight':1,'gamma':0,'subsample':0.8,
         'eval_metric':['merror','mlogloss'],'colsample_bytree':0.8, 
         'verbosity':0,'objective':'multi:softmax','num_class':3 }
num_round = 10
evals = [(dtrain,'train'),(dtest,'eval')]

bst = xgb.train(param, dtrain, num_round,evals = evals,)
y_ = bst.predict(dtest)
display(y_,accuracy_score(y_test,y_))   # 0.9722222222222222

算法差异:

传统GBDT以CART（gini系数进行裂分的决策树）作为基分类器，XGBoost还支持线性分类器，这个时候XGBoost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。
（经过GBDT推导，目前GBDT也是二阶导数）：传统GBDT在优化时只用到一阶导数信息，XGBoost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，XGBoost工具支持自定义代价函数，只要函数可一阶和二阶求导。
XGBoost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。正则降低了模型的方差，使学习出来的模型更加简单，防止过拟合，这也是XGBoost优于传统GBDT的一个特性。
Shrinkage（缩减），相当于学习速率（XGBoost中的eta）。XGBoost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）
列抽样（column subsampling）。XGBoost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是XGBoost异于传统GBDT的一个特性。
对缺失值的处理。对于特征的值有缺失的样本，XGBoost可以自动学习出它的分裂方向。
XGBoost工具支持并行。boosting不是一种串行的结构吗？怎么并行的？注意XGBoost的并行不是tree粒度的并行，XGBoost也是一次迭代完才能进行下一次迭代的。（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。XGBoost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分点）,XGBoost 在训练之前，预先对数据进行了排序，然后保存为Block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个Block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。

1、Xgboost介绍

1.1、Xgboost概述

XGBoost 是陈天奇等人开发的一个开源机器学习项目，高效地实现了GBDT算法并进行了算法和工程上的许多改进，被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。

1.2、青出于蓝

说到XGBoost，不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT，但是力争把速度和效率发挥到极致，所以叫X (Extreme) GBoosted。两者都是boosting方法。

2、Xgboost树的定义

2.1、构造决策树

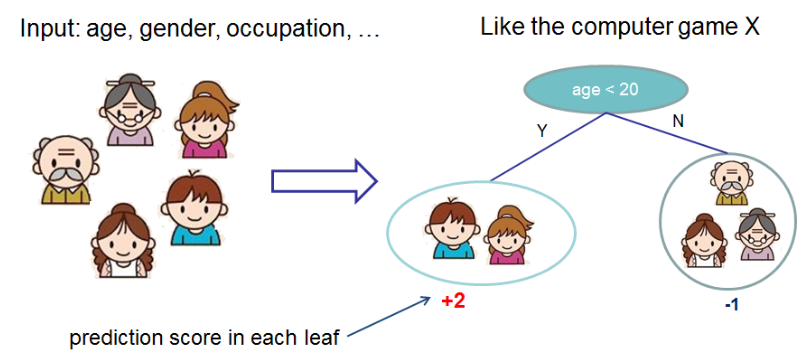
先来举个例子，我们要预测一家人对电子游戏的喜好程度，考虑到年轻和年老相比，年轻更可能喜欢电子游戏，以及男性和女性相比，男性更喜欢电子游戏，故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分，如下图所示。

2.2、决策树集成

就这样，训练出了2棵树tree1和tree2，类似之前gbdt的原理，两棵树的结论累加起来便是最终的结论，所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加：2 + 0.9 = 2.9。爷爷的预测分数同理：-1 + （-0.9）= -1.9。具体如下图所示：

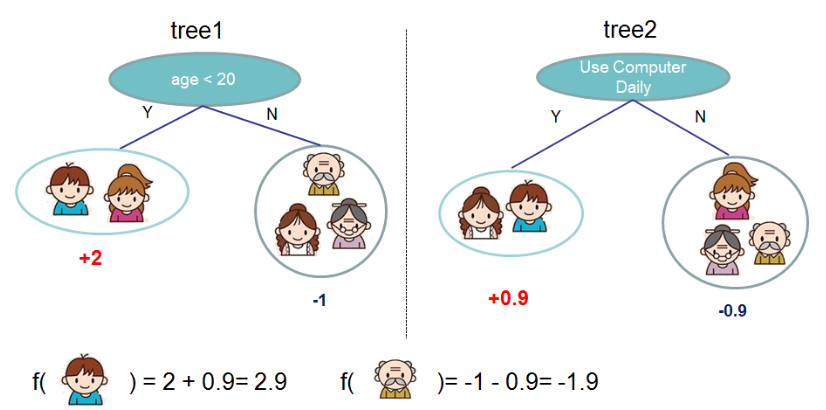
事实上，如果不考虑工程实现、解决问题上的一些差异，XGBoost与GBDT比较大的不同仅仅在于目标函数的定义。

3、Xgboost目标函数

3.1、目标函数方程

对于Boosting算法我们知道，是将多个弱分类器的结果结合起来作为最终的结果来进行输出。 $\small f_t(x_i)$ 为第 t 棵树的输出结果， $\small \hat{y}_i^{(t)}$ 是模型当前的输出结果，是实际的结果。

那么：

$\small \hat{y}_i^{(t)} = \sum\limits_{t=1}^t f_{t}(x_i)$

$\small \hat{y}_i^{(t)} = \hat{y}_i^{(t-1)} + f_t(x_i)$

XGBoost的目标函数如下图所示：

$\small Obj^{(t)} = \sum\limits_{i = 1}^nl(y_i,\hat{y}_i) + \sum\limits_{i =1}^t\Omega(f_t)$

训练损失 :

$\small \sum\limits_{i = 1}^nl(y_i,\hat{y}_i)$

常见损失函数 :

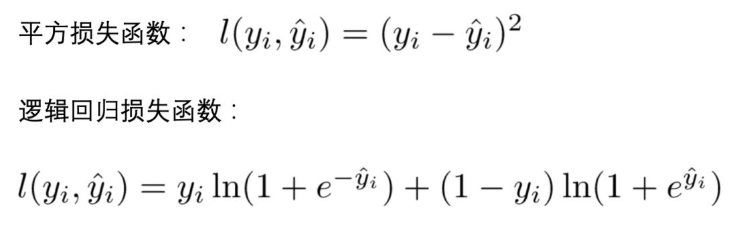
树的复杂度

$\small \sum\limits_{i =1}^t\Omega(f_i)$

Xgboost包含多棵树，定义每棵树的复杂度：

$\small \Omega(f) = \gamma T + \frac{1}{2}\lambda \sum\limits_{j=1}^T w_j^2$

$\small \sum\limits_{i=1}^{t-1}\Omega(f_i)$ 为前 t-1 棵树的复杂度，是常数项，求导时可忽略。目标函数简化为：

$\small Obj^{(t)} = \sum\limits_{i=1}^nl\left(y_i,\hat{y}_i^{t-1} + f_t{(x_i})\right) + \Omega(f_t)$

3.2、目标函数泰勒展开

泰勒展开近似目标函数：

$\small f(x + \Delta x) \approx f(x) + f'(x)\Delta x + \frac{1}{2}f''(x)\Delta x^2$

$\small Obj^{t} \approx \sum\limits_{i=1}^n\left[ l(y_i,\hat{y}_i^{(t-1)}) + g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)\right] + \Omega(f_t)$

方程中的 $\small l$ 即为损失函数（比如平方损失函数： $\small l(y_i,\hat{y_i}) = (y_i - \hat{y_i})^2$ ，或者交叉熵Log-loss
$\small \Omega(f_t)$ 的是正则项（包括L1正则、L2正则），防止过拟合，鲁棒性加强。
对于 f(x)，XGBoost利用二阶泰勒展开三项，做一个近似。f(x)表示的是其中一颗回归树。

由于在第 t 步时 $\small \hat{y}_i^{(t-1)}$ 其实是一个已知的值，所以 $\small l(y_i,\hat{y}_i^{(t-1)})$ 是一个常数，其对函数的优化不会产生影响。因此，去掉全部的常数项，得到目标函数为：

$\small Obj^{t} \approx \sum\limits_{i=1}^n\left[g_if_t(x_i) + \frac{1}{2}h_if^2_t(x_i)\right] + \Omega(f_t)$

所以我们只需要求出每一步损失函数的一阶导和二阶导的值（由于前一步的 $\small \hat{y}^{(t-1)}$ 是已知的，所以这两个值就是常数），然后最优化目标函数，就可以得到每一步的 $\small f(x)$ ，最后根据加法模型得到一个整体模型。

3.3、定义一棵树

我们重新定义一颗树，包括两个部分：

叶子结点的权重向量；
实例 ---> 叶子结点的映射关系q（本质是树的分支结构）；

3.4、定义树的复杂度

我们定义一颗树的复杂度 $\small \Omega$ ，它由两部分组成：

叶子结点的数量；
叶子结点权重向量的L2范数；

3.5、叶子结点归组

我们将属于第 j 个叶子结点的所有样本 xi , 划入到一个叶子结点样本集中，数学表示如下：

$\small I_j = {i|q(x_i) == j}$

3.6、树结构打分

回忆一下高中数学知识。假设有一个一元二次函数，形式如下：

$\small Gx + \frac{1}{2}Hx^2, H > 0$

我们可以套用一元二次函数的最值公式轻易地求出最值点：

上图给出目标函数计算的例子，求每个节点每个样本的一阶导数和二阶导数，然后针对每个节点对所含样本求和得到和，最后遍历决策树的节点即可得到目标函数。

4、Xgboost模型使用

4.1、模型基本使用

4.1.1、使用方式一

import numpy as np
import xgboost as xgb
from xgboost import XGBClassifier
from sklearn import datasets
from sklearn import tree
from sklearn.model_selection import train_test_split
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
model = XGBClassifier(
    learning_rate =0.1, # 学习率，控制每次迭代更新权重时的步长，默认0.3。值越小，训练越慢
    use_label_encoder=False,
    n_estimators=10,   # 总共迭代的次数，即决策树的个数
    max_depth=5,       # 深度
    min_child_weight=1,  # 默认值为1,。值越大，越容易欠拟合；值越小，越容易过拟合
    gamma=0,        # 惩罚项系数，指定节点分裂所需的最小损失函数下降值。
    # 训练每棵树时，使用的数据占全部训练集的比例。默认值为1，典型值为0.5-1。防止overfitting
    subsample=0.8,  
    colsample_bytree=0.8,
    objective= 'binary:logistic',  # 目标函数
    eval_metric = ['merror'],  # 验证数据集评判标准
    nthread=4,)    # 并行线程数
eval_set = [(X_test, y_test),(X_train,y_train)]
model.fit(X_train,y_train,eval_set = eval_set,verbose = True)
model.score(X_test,y_test)     # 0.9722222222222222

4.1.2、使用方式二：

X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
param = {'learning_rate':0.1,'n_estimators':10,
         'max_depth':5,'min_child_weight':1,'gamma':0,'subsample':0.8,
         'colsample_bytree':0.8, 'verbosity':0,'objective':'multi:softprob'}
model = xgb.XGBClassifier(**param)
model.fit(X_train, y_train, early_stopping_rounds=20, eval_metric='merror',
        eval_set=[(X_test, y_test)])
model.score(X_test,y_test)

4.1.3、使用方式三

DMatrix是XGBoost中使用的数据矩阵。DMatrix是XGBoost使用的内部数据结构，它针对内存效率和训练速度进行了优化。

import xgboost as xgb
from sklearn.metrics import accuracy_score
X,y = datasets.load_wine(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)

# 创建数据
dtrain = xgb.DMatrix(data = X_train,label = y_train)
dtest = xgb.DMatrix(data = X_test,label = y_test)
# 指定参数
param = {'learning_rate':0.1,'use_label_encoder':False,'n_estimators':20,
         'max_depth':5,'min_child_weight':1,'gamma':0,'subsample':0.8,
         'eval_metric':['merror','mlogloss'],'colsample_bytree':0.8, 
         'verbosity':0,'objective':'multi:softmax','num_class':3 }
num_round = 10
evals = [(dtrain,'train'),(dtest,'eval')]
bst = xgb.train(param, dtrain, num_round,evals = evals,)
# 进行预测
y_ = bst.predict(dtest)
display(y_,accuracy_score(y_test,y_))   # 0.9722222222222222