CSDN每日一练：小豚鼠搬家

news2025/2/24 5:52:40

题目名称：小豚鼠搬家
时间限制：1000ms内存限制：256M

题目描述
小豚鼠排排坐。小艺酱买了一排排格子的小房子n*m，她想让k只小豚鼠每只小豚鼠都有自己的房子。但是为了不浪费空间，她想要小房子的最外圈尽量每行每列都有一只小豚鼠居住。小艺酱想知道自己有多少种方案安排小豚鼠。

输入描述：
输入整数n,m,k。(1<=n,m<=20,0<=k<=n*m)

输出描述：
输出方案数，答案对1e9+7取模。

示例
示例1
输入
3 3 2
输出
2

提示
无

用例里有两个比较特殊，一个是没有豚鼠的用例，[3, 4, 0]，这个如果用递归的话，需要避免这个用例，豚鼠数字小于2，就返回0，笼子就1个格，返回1

另一个就是真正的算法考验的用例了 [5, 5, 12]，返回结果是 4704606…我在本地跑了一下，最土的递归用了一分半钟左右才得出这个结果

先放第一版的

def s(row,col,num,start,pos):
    #result = []
    result = 0
    if num == 1:
        for i in range(start,row*col):
            t = pos + [i]
            if len([_ for _ in t if _ // col == 0])>0 and len([_ for _ in t if _ % col == 0])>0 and len([_ for _ in t if _ // col == row-1])>0 and len([_ for _ in t if _ % col == col - 1])>0:
                #result.append(pos + [i])
                result += 1
        return result
    else:
        for i in range(start,row*col-num+1):
            result += s(row,col,num-1,i+1,pos+[i])
    return result


n,m,k = [4,4,14]
result = s(n,m,k,0,[])

于是就想起来，好像看到过某个文章里讲解了这个题目怎么算，完全不用递归组合什么的，就是数学公式，最后找了半天也没找到之前看到的文章，但还是搜索出了一个类似的，讲解的也比较清楚的文章

https://www.cnblogs.com/pengwill/p/7367030.html

文章的意思就是用最大组合减去不合要求的组合，再加上遗漏的组合，再减去遗漏组合中不合要求的组合。。。嗯，用循环完成的，叫什么容斥原理。。。原谅老顾没上过学。。。。

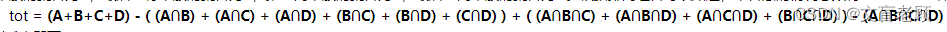
在这里插入图片描述
具体为什么程序这么写倒是没搞明白，尤其是中间用到位运算，怎么就和这总计的16项（最大集合，及15个容斥原理对应内容）

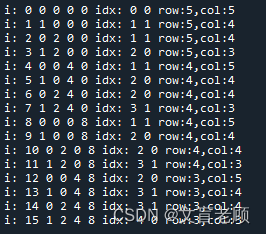
最后还是列了个输出信息才弄明白，哪些是加的，哪些是减的，分别加了多少减了多少。。。。嗯，只需要一个阶乘函数，一个组合函数就够了

n,m,k = [5,5,12]

total = 0

for i in range(16):
    idx = 0
    row = n
    col = m
    if i & 1: # 对应集合 A，最上边一行无小鼠
        col -= 1
        idx += 1
    if i & 2: # 对应集合 B，最下边一行无小鼠
        col -= 1
        idx += 1
    if i & 4: # 对应集合 C，最左边一列无小鼠
        row -= 1
        idx += 1
    if i & 8: # 对应集合 D，最右边一列无小鼠
        row -= 1
        idx += 1
    print('i:',i,i&1,i&2,i&4,i&8,'idx:',idx,idx & 1,'row:{},col:{}'.format(row,col))
    if idx & 1:
        total -= int(X(row*col,k))
    else:
        total += int(X(row*col,k))

print(total)