机器学习：从数据中学习知识；

1. 原始数据中提取特征；
2. 学习映射函数f；
3. 通过映射函数f将原始数据映射到语义空间，即寻找数据和任务目标之间的关系；

机器学习：

• 监督学习：数据有标签，一般为回归或分类等任务；
• 无监督学习：数据无标签，一般为聚类或若干降维任务；
• 强化学习：序列数据决策学习，一般为从环境交互中学习；

4.1 监督学习

监督学习的重要元素：

• 标注数据：表示了类别信息的数据；
• 学习模型：如何学习得到映射模型；
• 损失函数：如何对学习结果进行度量；

损失函数：

• 训练集中一共有n个标注数据，第i个标注数据记为（xi，yi）其中第i个样本数据为xi，yi是xi的标注信息。
• 从训练数据中学习得到的映射函数记为f，f对xi的预测结果记为f(xi)。损失函数就是用来计算xi真实值yi与预测值f(xi)之间差值的函数。
• 很显然，在训练过程中希望映射函数在训练数据集上得到的损失之和最小。

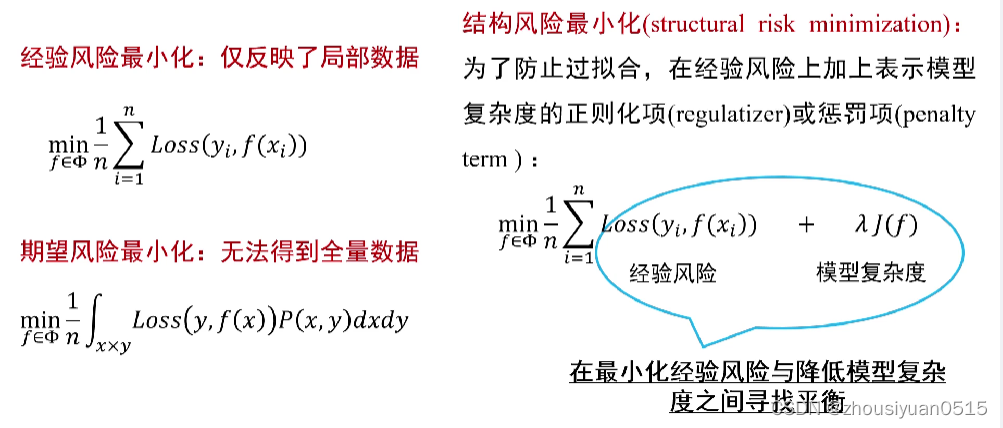
经验风险：训练集中数据产生的损失。经验风险越小说学习模型对训练数据拟合程度越好。

期望风险：当测试集中存在无穷多数据时产生的损失。期望风险越小，学习所得模型越好。

• 映射函数训练目标：经验风险最小化，期望风险最小化；
• 期望风险是模型关于联合分布期望损失，经验风险是模型关于训练样本集平均损失。
• 根据大数定律，当样本容量趋于无穷时，经验风险趋于期望风险。所以在实践中很自然用经验风险来估计期望风险。
• 由于现实中训练样本数目有限，用经验风险估计期望风险并不理想，要对经验风险进行一定的约束。

过学习与欠学习

经验风险小（训练集上表现好）	期望风险小（测试集上表现好）	泛化能力强
经验风险小（训练集上表现好）	期望风险大（测试集上表现不好）	过学习（模型过于复杂）
经验风险大（训练集上表现不好）	期望风险大（测试集上表现不好）	欠学习
经验风险大（训练集上表现不好）	期望风险小（测试集上表现好）	神仙算法或黄粱美梦

判别模型与生成模型

监督学习方法又可以分为生成方法和判别方法。所学到的模型分别称为生成模型和判别模型。

• 判别方法直接学习判别函数f(X)或者条件概率分布P(Y|X)作为预测的模型，即判别模型；
• 判别模型关心在给定输入数据下，预测该数据的输出是什么。
• 经典判别模型包括回归模型、神经网络、支持向量机和Ada boosting等。
• 生成模型从数据中学习联合概率分布P(X,Y)（通过似然概率P(X|Y)和类概率P(Y)的乘积来求取）P(Y|X) = P(X,Y) / P(X) 或者P(Y|X) = P(X|Y) * P(Y) / P(X)
• 联合分布概率P(X,Y) 或似然概率P(Y|X)求取很困难
• 贝叶斯方法P(Y|X) = P(X|Y) * P(Y) / P(X)

4.2 线性回归分析

线性回归：

• 在现实生活中，往往需要分析若干变量之间的关系，如碳排放量与气候变暖之间的关系、商品广告投入量与该商品销售量之间的关系等，这种分析不同变量之间存在关系的研究叫回归分析，刻画不同变量之间关系的模型被称为回归模型。如果这个模型是线性的，则称为线性回归模型。
• 一旦确定了回归模型，就可以进行预测等分析工作。

参数学习：回归模型参数求取：yi = axi + b (1 <= i <= n)

4.3 提升算法（adaptive boosting，自适应提升）

• 对于一个复杂的分类任务，可以将其分解为若干子任务，然后将若干子任务完成方法综合，最总完成该复杂任务。
• 将弱分类器组合起来，形成强分类器。

计算学习理论

霍夫丁不等式

概率近似正确

对于统计电视节目收视率这样的任务，可以通过不同的采样方法（即不同模型来计算收视率），每个模型会产生不同的误差。

在概率近似正确背景下，有强可学习模型和弱可学习模型。

强可学习	学习模型能够以较高精度对绝大多数样本完成识别分类任务
弱可学习	学习模型仅能完整若干部分样本识别与分类，其精度略高于随机猜测
强可学习和弱可学习是等价的，也就是说，如果已经发现了弱学习算法，可将其提升为强学习算法。Ada Boosting算法就是这样的方法。具体而言，Ada Boosting将一系列弱分类器组合起来，构成一个强分类器。

Ada Boosting

Ada Boosting中两个核心问题：

• 在每个弱分类器学习过程中，如何改变训练数据的权重：提高在上一轮中分类错误样本的权重。
• 如何将一系列弱分类器组合成强分类器：通过加权多数表决方法来提高分类误差小的弱分类器的权重，让其在最终分类中起到更大作用。同时减少分类误差大的弱分类器的权重，让其在最终分类中仅起到较小作用。

算法描述：

 算法解释：

 

 

回归与分类的区别：

• 两者均是学习输入变量和输出变量之间潜在关系模型，基于学习所得模型将输入变量映射到输出变量。
• 监督学习分为回归和分类两个类别。
• 在回归分析中，学习得到一个函数将输入变量映射到连续输出空间，值域是连续空间；
• 在分类模型中，学习得到一个函数将输入变量映射到离散输出空间，值域是离散空间；

4.4 无监督学习

K均值聚类（K-means聚类）

输入：n个数据（无任何标注信息）

输出：k个聚类结果

目的：将n个数据聚类到k个集合（也成为类簇）

算法描述：

 算法：

1.初始化聚类质心

2.将每个待聚类数据放入唯一一个聚类集合中

3.根据每个聚类集合中所包含的数据，更新该聚类集合质心值

4.算法循环迭代，直到满足条件

• 在新聚类质心基础上，根据欧式距离大小，将每个待聚类数据放入唯一一个聚类集合中
• 根据新的聚类结果、更新聚类质心
• 聚类迭代满足以下条件，则聚类停止：已经达到了迭代次数上线；在前后两次迭代中，聚类质心保持不变。

K均值聚类算法的另一个视角：最小化每个类簇的方差

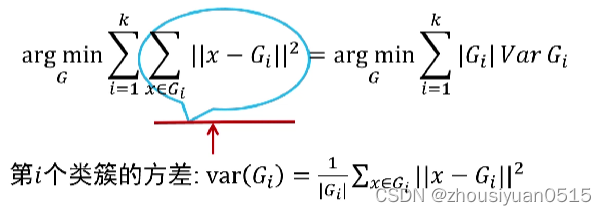
• 欧式距离与方差量纲相同
• 最小化每个类簇方差将使得最终每个聚类结果中每个聚类集合中所包含的数据呈现出来的差异最小

不足：

• 需要实现确定聚类数目，很多时候我们并不知道数据应被聚类的数目；
• 需要初始化聚类质心，初始化聚类中心对聚类结果有较大的影响；
• 算法是迭代执行，时间开销非常大；
• 欧式距离假设数据每个维度之间的重要性是一样的；

主成分分析

主成分分析是一种特征降维方法，降维后的结果要保持原始数据固有结构。

原始数据中的结构：

• 图像数据中结构：视觉对象区域构成的空间分布；
• 文本数据中解雇：单词之间的（共现）相似或不相似；

方差

• 方差等于各个数据与样本均值之差的平方和之平均数；
• 方差描述了样本数据的波动程度；

协方差

• 衡量两个变量之间的相关度

• 当协方差cov(X, Y) > 0，称X与Y正相关；
• 当协方差cov(X, Y) < 0，称X与Y负相关；
• 当协方差cov(X, Y) = 0，称X与Y不相关（线性意义下）

相关系数

我们可以通过皮尔孙相关系数将两组变量之间的关联度规整到一定的取值范围内：

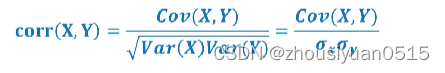
主要性质：

• 绝对值小于等于1；
• corr(X, Y) = 1的充要条件是存在常数a和b，使得Y = aX + b；
• 相关系数是对称的；
• 相关值越大，相关程度越大；

算法动机

• 在数理统计中，方差被经常用来度量数据和其数学期望（即均值）之间的偏离程度，这个偏离程度反映了数据分布结构；
• 在许多实际问题中，研究数据和其均值之间的偏离程度有着很重要的意义；
• 在降维之中，需要尽可能将数据向方差最大方向进行投影，使得数据所蕴含信息没有丢失，展现个性；
• 主成份分析思想是将n维特征数据映射到l维空间（n >> l），去除原始数据之间的冗余性（通过去除相关性达到这一目的）
• 将原始数据向这些数据方差最大的方向进行投影。一旦发现了方差最大的投影方向，则继续寻找保持方差第二的方向且进行投影；
• 将每个数据从n维高位空间映射到l维低维空间，每个数据所得到最好的k维特征就是使得每一维上样本方差都尽可能大。

 

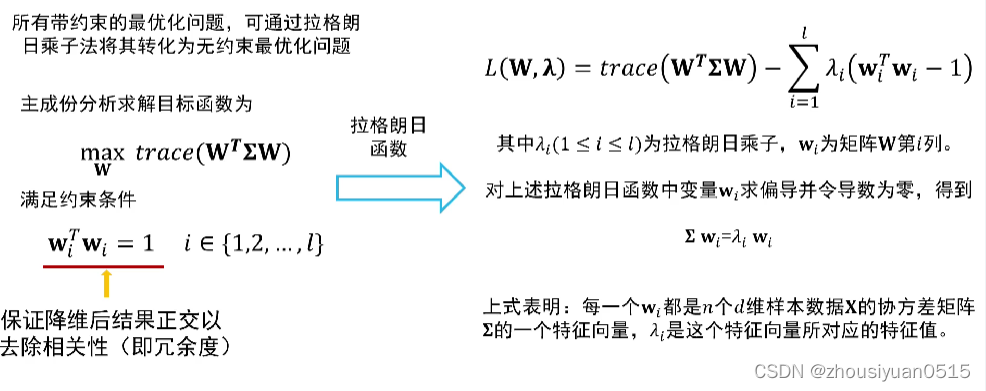
算法描述

输入：n个d维样本数据所构成的矩阵X，降维之后的维数l

输出：映射矩阵

算法步骤：

 

特征人脸算法

特征人脸方法是一种应用主成份分析来实现人脸图像降维的方法，其本质使用一种特征人脸的特征向量按照线性组合形式来表达每一张原始人脸图像，进而实现人脸识别。（用特征人脸表示人立案，而非用像素点表示人脸）

算法描述

• 将每幅人脸图像转换成列向量
• 将一幅32 * 32 的人脸图像转成1024 * 1的列向量

输入：n个1024维人脸样本所构成的矩阵X，降维后的维数l

输出：映射矩阵

算法步骤：

• 每个人脸特征向量与原始人脸数据的维数是一样的，均为1024；
• 可将每个特征向量还原为32 * 32的人脸图像，称之为特征人脸，因此可得到l个特征人脸。

基于特征人脸的降维：

• 将每幅人脸分别与每个特征人脸做矩阵乘法，得到一个相关系数；
• 每幅人脸得到l个相关系数（从n维降到l维）
• 由于每幅人脸是所有特征人脸的线性组合，因此就实现人脸从像素点表达到特征人脸表达的转变。
• 使用l个特征人脸的线性组合来表达原始人脸数据
• 在后续人脸识别分类中，就使用l个系数来表示原始人脸图像。即计算两张人脸是否相似，不是去计算两个32 * 32矩阵是否相似，而是计算两个人脸所对应的l个系数是否相似

人脸表达方式对比：

• 聚类表示：用待表示人脸最相似的聚类质心来表示；
• 特征人脸表示：使用l个特征人脸的线性组合来表达原始人脸数据；
• 非负矩阵人脸分解方法表示：通过若干个特征人脸的线性组合来表达原始人脸数据，体现了部分组成整体。

统计机器学习算法应用

逻辑斯蒂回归与分类

回归和分类均是挖掘和学习输入变量和输出变量之间的潜在关系模型，基于学习所得模型将输入变量映射到输出变量。

• 在回归分析中，学习得到一个函数将输入变量映射到连续输出空间，即值域是连续空间。
• 在分类模型中，学习得到一个函数将输入变量映射到离散输出空间，即值域是离散空间。

逻辑斯蒂回归就是在回归模型中引入sigmoid函数的一种非线性回归模型。

Logistic回归模型：

sigmoid函数

• 概率形式输出。sigmoid函数是单调递增的，其值域为(0, 1)，因此使sigmoid函数输出可作为概率值。
• 数据特征加权累加。对输入z取值范围没有限制，但当z大于一定数值后，函数输出无限趋近于1，而小于一定数值后，函数输出无限趋近于0。当z = 0时，函数输出为0.5。这里z时输入数据x和回归函数的参数w相乘结果（可视作x各维度进行加权叠加）
• 非线性变化。x各维度加权叠加之和结果取值在0附近时，函数输出值的变化幅度比较大（函数值变化陡峭），且时非线性变化。但是，各维度加权叠加之和结果取值很大或很小时，函数输出值几乎不变化，这是基于概率的一种认识与需要。

回归到分类：概率输出

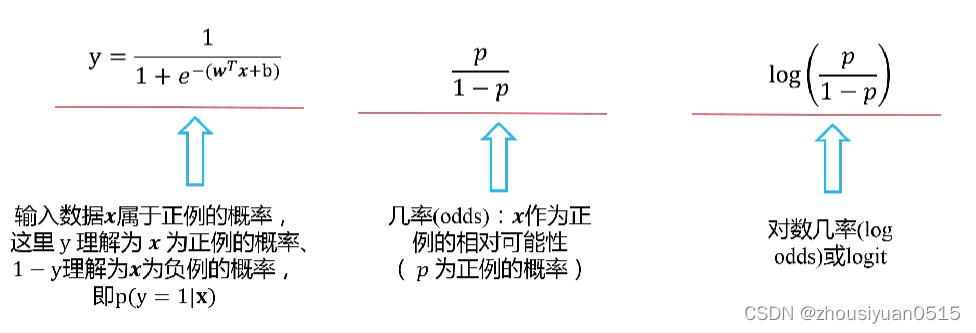
• 对数几率回归模型的输出y可作为输入数据x分类为某一类别概率的大小；
• 输出值越接近于1，说明输入数据x分类为该类别的可能行越大。与此相反，输出值越接近0，输入数据x不属于该类别的概率越大。
• 根据具体应用设置一个阈值，将大于该阈值的输入数据x都归属到某个类别，小于该阈值的输入数据都归属到另外一个类别。
• 如果输入数据x属于正例的概率大于属于负例的概率，则输入数据x可被判断属于正例。
• logistic回归是一个线性模型，在预测时们可以通过计算线性函数取值是否大于0来判断输入数据x的类别归属。

从回归到分类：参数求取

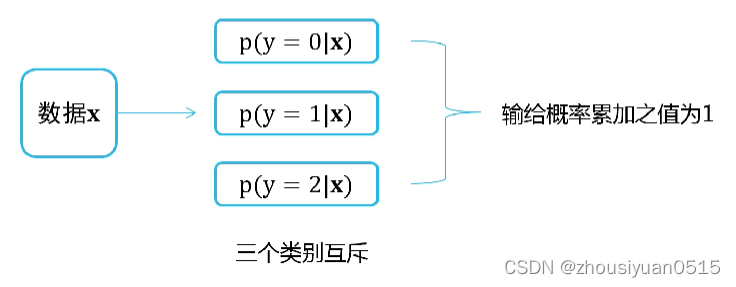
从回归到分类（softmax分类）：从两类分类到多类分类

logistic回归只能用于解决二分类问题，将他进行推广为多项逻辑斯蒂回归模型，用于处理多类分类问题，可以得到处理多类分类问题的softmax回归。

 

潜在语义分析

潜在语义分析（LSI）时一种从海量文本数据中学习单词-单词、单词-文档以及文档-文档之间隐性关系，进而得到文档和单词表达特征的方法。该方法的基本思想时综合考虑某些单词在哪些文档中同时出现，以此来决定该词语的含义与其他的词语的相似度。

潜在语义分析先构建一个单词-文档矩阵A，进而寻找该矩阵的低秩逼近，来挖掘单词-单词、单词-文档以及文档-文档之间的关联关系。

构造与分解

歧义值分解：将一个矩阵分解为两个正交矩阵与一个对角矩阵的乘积。

• A = UDVt，单词个数为M、文档个数为N
• 将每个单词映射到维度为R的隐性空间，将每个文档映射到维度为R的隐性空间：统一空间
• 隐性空间可视为主题空间

 

线性区别分析及分类

线性区别分析（LDA）是一种基于监督学习的降维方法，也成为FIsher线性区别分析（FDA）。

对于一组具有标签信息的高维数据样本，LDA利用其类别信息，将其线性投影到一个低维空间上，在低维空间中同一类别样本尽可能靠近，不同类别样本尽可能彼此远离。

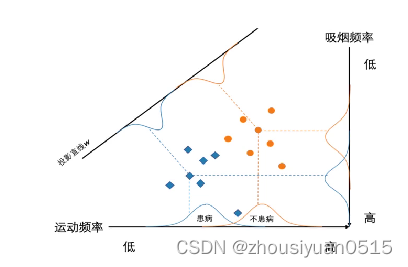
• 协方差矩阵s1和s2可用来衡量同一类别数据样本之间分散程度。为了使得归属于同一类别的样本数据在投影后的空间中尽可能靠近，需要最小化s1 + s2

• 主成份分析（PCA）是一种无监督学习的降维方法（无需样本类别标签），线性区别分析（LDA）是一种监督学习的降维方法（需要样本类别标签）。PCA和LCA均是优化寻找一定特征向量w来实现降维，其中PCA寻找投影后数据之间方差最大的投影方向、LDA寻找类内方差小、类间距离大的投影方向。
• PCA对高维数据降维后的维数是与原始数据特征维度相关（与数据类别标签无关）。假设原始数据维度是d，那么PCA多的数据的降维维度可以为小于d的任意维度。LDA降维后所得到的维度是与数据样本的类别个数K有关（与数据本身的维度无关）。假设原始数据一共有k个类别，那么LDA所得数据的降维维度小于或等于k - 1.

高维数据降维方法的种类

如何从高维数据中获取其蕴含的本质属性信息，即将高维数据转换到低维空间，同时保留其高维空间所具有的属性，是当前学术界的研究热点问题。按照不同的标准，高维数据的降维算法可分为如下不同种类：

1. 线性降维与非线性降维。这一方法根据降维算法是否通过线性映射或非线性映射实现而区分。线性降维方法主要包括主成分分析（Principal Component Analysis, PCA）、多维尺度分析（Metric multidimensional scaling, MDS）、线性判别分析（Linear Discriminant Analysis, LDA），其主要思路是在原始空间设计得到一系列特征向量，然后通过对这些特征向量进行线性组合来达到高维特征降维目的。线性降维的优点在于其通过简单变换函数实现原始高维数据降维。但是，原始高维数据往往分布在一个“非线性特征”空间中（如数据分布在曲线中或曲面上等），原始数据的非线性分布将使得直接应用线性降维变得不合时宜，也就是说线性降维将失效。为了解决这一问题，相应地出现了一些非线性高维特征降维方法，如等距映射（Isometric Mapping，ISOMAP）、局部线性嵌入（Locally Linear Embedding，LLE）、拉普拉斯特征映射（Laplacian Eigenmap）和局部不变投影（Locally Preserving Projections, LPP）等方法，这些非线性降维方法通过挖掘高维数据在原始空间中所具有的流形、拓扑和几何等属性，进而形成保持这些属性的非线性降维方法。
2. 局部保持降维与全局保持降维。局部保持降维意味着该类降维方法将使得降维后数据之间局部信息与原始数据之间局部信息得以保持，比如任意两个高维数据在原始空间相互邻近，则在降维后的空间中这两个高维数据之间距离仍然相近，这类方法包括局部线性嵌入（LLE）和局部不变投影（LPP）等降维方法。与局部保持降维相反，全局保持降维则意味着任意两个高维数据在原始空间全局距离较近，则在降维后的空间中这两个高维数据之间的全局距离仍较近。全局保持降维的方法包括等距映射（ISOMAP）和主成份分析（PCA）等。
3. 监督学习降维和非监督学习降维。监督学习降维是指在降维过程中利用了样本所具有的类别信息，而非监督学习则未利用样本具有的类别信息。主成份分析（PCA）和局部不变投影（LPP）等可归属为无监督降维算法，线性区别分析（Linear Discriminant Analysis, LDA）则为监督降维算法。