万字手撕AVL树 | 上百行的旋转你真的会了吗？【超用心超详细图文解释 | 一篇学会AVL】

news2024/11/29 4:38:29

说在前面

今天这篇博客，是博主今年以来最最用心的一篇博客。我们也很久没有更新数据结构系列了，几个月前博主用心深入的学习了这颗二叉平衡搜索树，博主被它的查找效率深深吸引。

AVL树出自1962年中的一篇论文《An_algorithm_for_the_organization_of_information》，它解决了普通二叉搜索树退化的问题，这个博主稍后会详细解释。AVL树放到现在，它的查找效率是很少数据结构能够比拟的。

博主为了这篇博客，做了很多准备，试了很多画图软件，就是为了让大家看得明白！希望大家不要吝啬一键三连啊！！

前言

那么这里博主先安利一下一些干货满满的专栏啦！

手撕数据结构https://blog.csdn.net/yu_cblog/category_11490888.html?spm=1001.2014.3001.5482这里包含了博主很多的数据结构学习上的总结，每一篇都是超级用心编写的，有兴趣的伙伴们都支持一下吧！
算法专栏https://blog.csdn.net/yu_cblog/category_11464817.html这里是STL源码剖析专栏，这个专栏将会持续更新STL各种容器的模拟实现。

STL源码剖析https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482

什么是AVL树？

tips：博主在最后会放一份整体代码，供大家参考！

首先，它是一颗二叉搜索树。

什么是二叉搜索树：

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  • 它的左右子树也分别为二叉搜索树

如图所示：这就是一颗二叉搜索树。

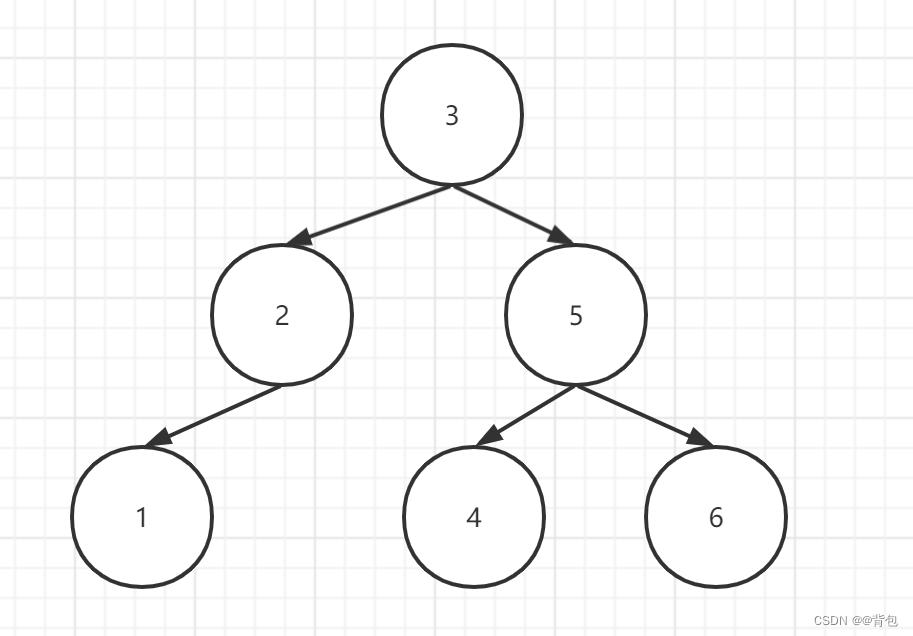
当我们需要在这颗搜索树里面查找节点4的时候，我们从3开始，比3大，往右走，比5小，往左走。这样我们就找到了4这个节点。

一颗二叉搜索树最高的查找复杂度是O(h)，h为树的高度，这样其实我们也可以得到较好的查找效率了。但是，搜索树可能会退化。如图所示：

 

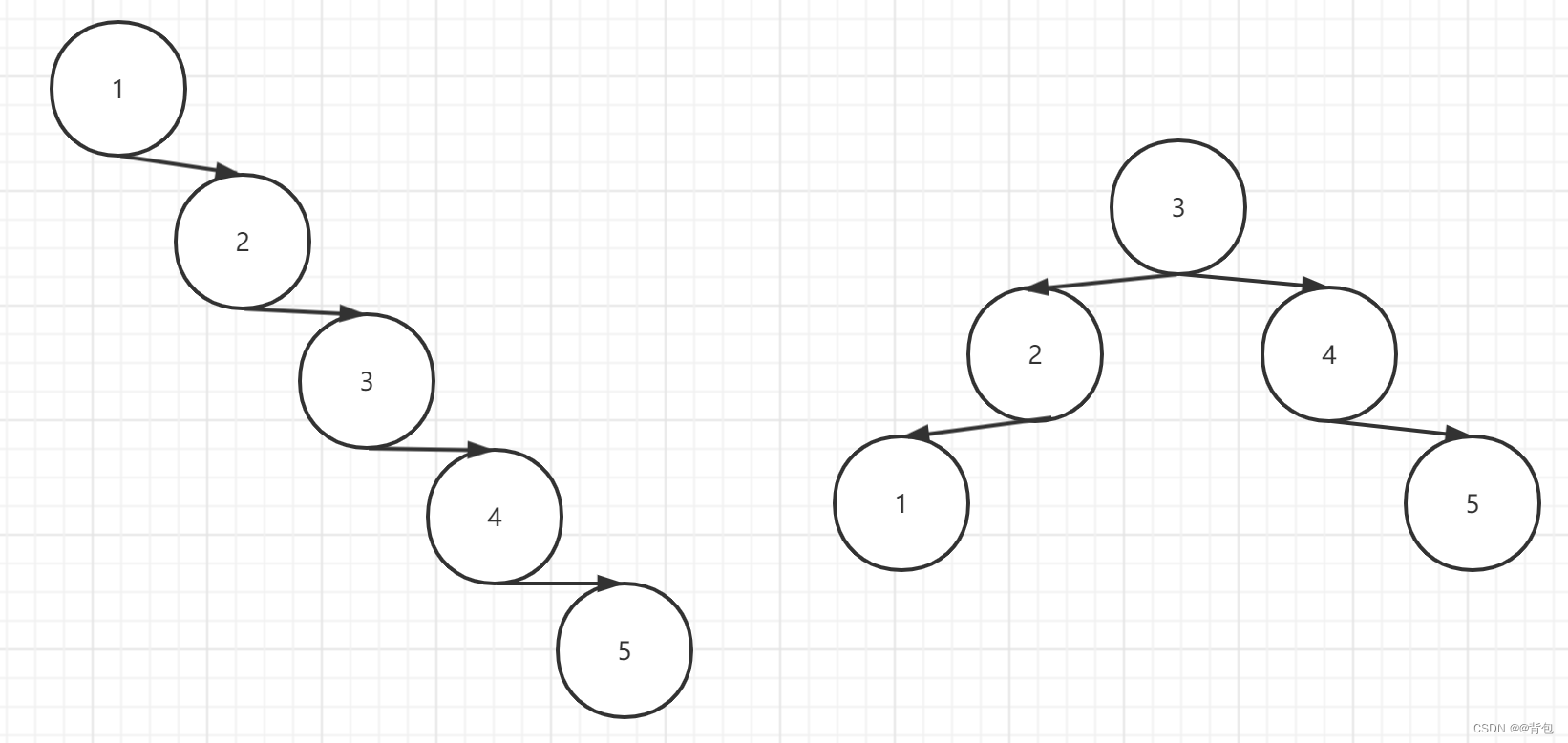
比如第一棵树，我们如果要查找最下面那个节点，我们要找n次。比如第二棵树，我们找最下面节点要找n/2次，假设我们要查10亿个数据，我们要找5亿次，其实还是O(n)级别。在这种情况下，查找就没有优势了。导致这种情况的主要原因就是，高度不平衡！我们设想一颗满二叉树，它就是平衡的，我们查找一个值，即高度次，复杂度是O(logn)。因此我们需要在插入的同时，不断变换这颗树，使它的高度平衡，这样我们的查找性能才能得到质的提升！一颗二叉平衡搜索树，在10亿个数据中查找一个值，最多查找31次，这种优化，是非常大的！

因此我们引出二叉平衡搜索树，常见的二叉平衡搜索树有AVL树和红黑树。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

  • 它的左右子树都是AVL树
  • 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
  • 平衡因子 = 右子树高度 - 左子树高度

 

 AVL树的结构定义

AVL树通常使用三叉链进行构造，我们在处理指针的时候要记得_parent也要处理。

template<class K,class V>
struct AVLNode {
public:
	AVLNode<K, V>* _left;
	AVLNode<K, V>* _right;
	AVLNode<K, V>* _parent;
	pair<K, V>_kv;
	int _bf;  //balance factor
public:
	AVLNode(const pair<K, V>& kv)
		:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0) {}
};

template<class K, class V>
struct AVL {
	typedef AVLNode<K, V>Node;
private:
	Node* _root = nullptr;
public:
    //成员函数
    //...
}

AVL树节点的插入（重点）

AVL树的节点插入可以分为三个步骤：

  1. 新节点的插入
  2. 平衡因子的更新
  3. 通过平衡因子确定平衡性是否被打破，若平衡性被打破，进行旋转

AVL树的旋转：

  1. 左单旋
  2. 右单旋
  3. 左右双旋
  4. 右左双旋

AVL树的旋转是本篇博客最最最最最重点的地方，博主将会详细解释这部分！

一、新节点的插入

新节点的插入步骤和普通二叉搜索树的插入步骤一样，找到插入的位置，直接插入即可！

	bool insert(const pair<K, V>& kv) {
		if (_root == nullptr) {
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur) {
			if (cur->_kv.first < kv.first) {
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first) {
				parent = cur;
				cur = cur->_left;
			}
			else return false;
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first) {
			parent->_right = cur;
		}
		else  {
			parent->_left = cur;
		}
		cur->_parent = parent;

		//先更新平衡因子
		//...
        //平衡因子更新后，判断是否需要旋转

		return true;
	}

二、更新平衡因子

当一个新节点被插入之后，该节点的祖先路径上的节点有可能会受到影响，我们要看情况进行更新。如图所示：插入节点后，只会影响祖先路径上节点的平衡因素。

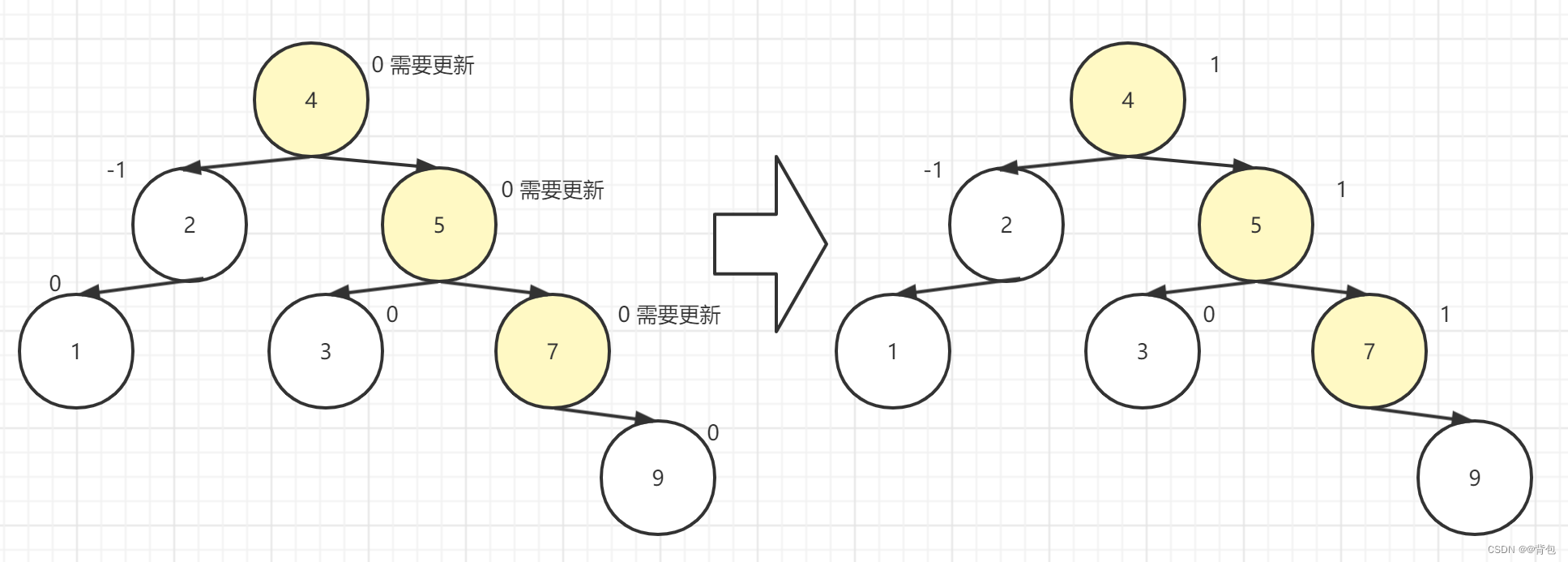
 我们只需要利用_parent指针，不断迭代向上就行了。

  • 如果插入在「新节点父亲」的右边，父亲的平衡因子++
  • 如果插入在「新节点父亲」的左边，父亲的平衡因子 - -

tips：博主在最后会放一份整体代码，供大家参考！

如果平衡因子更新后是1/-1，说明子树的高度被改变了，需要继续向上迭代。如果平衡因子更新后是0，说明新节点只是把子树不齐的地方补齐了（这个很好理解，如果大家不明白可以简单画个图），如果更新后平衡因子是2/-2，说明平衡被打破了，需要旋转

        while (parent) {//只有根没有父亲
			//最坏可能需要更新到根
			if (cur == parent->_right) {
				parent->_bf++;
			}
			else {
				parent->_bf--;
			}

			if (parent->_bf == 0) {
				//高度不变 -- 停止更新
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1) {
				//继续更新
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2) {
				//说明parent所在的子树已经不平衡了 -- 需要旋转
			}
			else {
				assert(false);//理论上不能走到这里
			}
		}

三、旋转

AVL树的旋转：

  1. 左单旋
  2. 右单旋
  3. 左右双旋
  4. 右左双旋

首先我们来看几个例子，大概了解一下旋转是一个什么样的操作，看下旋转式怎么让不平衡的树便平衡的:

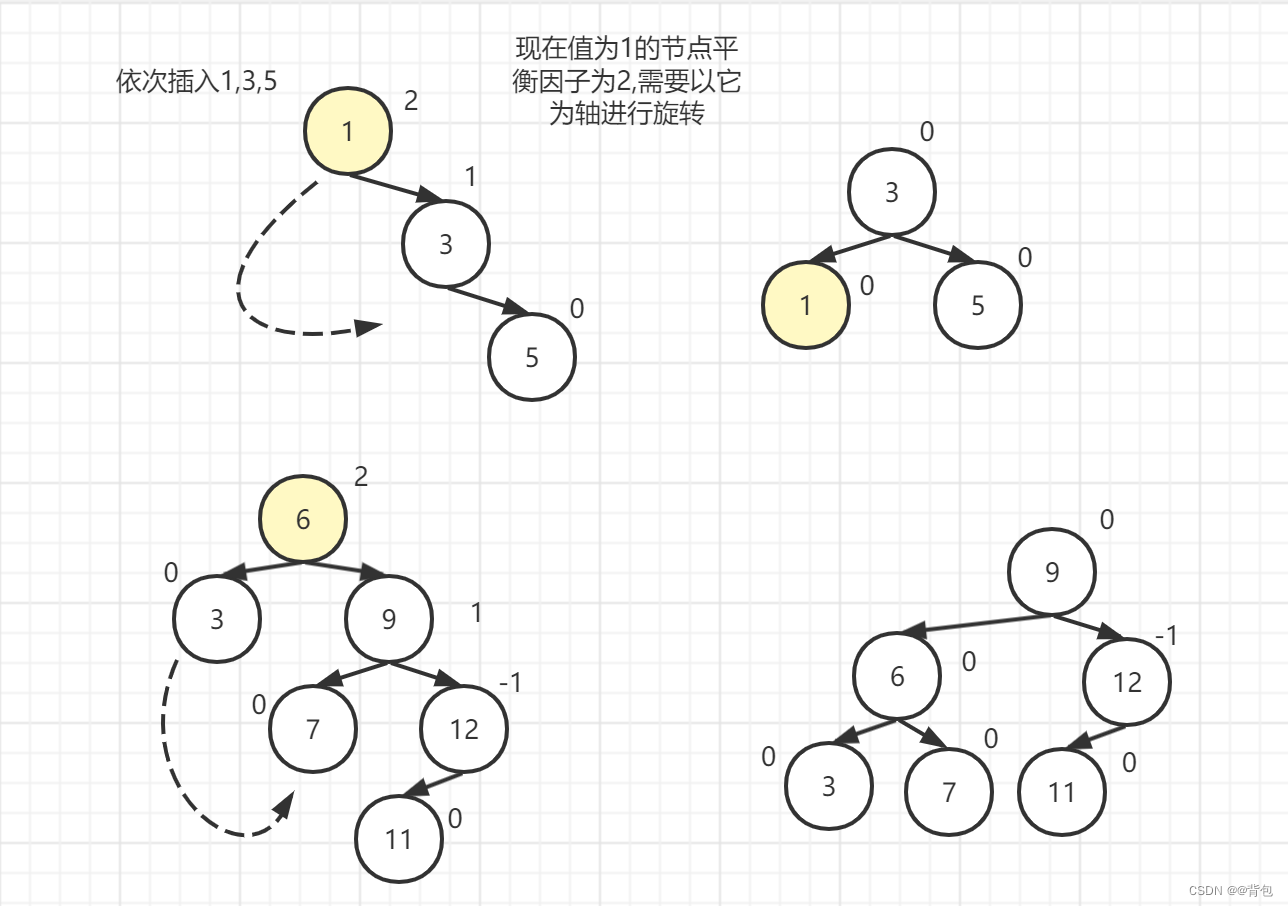
 这里只展示了旋转中的其中一种情况,左单旋,现在博主将分四种情况给大家详细讲解

左单旋:新节点插入较高右子树的右侧

大家注意,这里的触发条件是,较高的是右子树,而且插入的是在该右子树的右侧

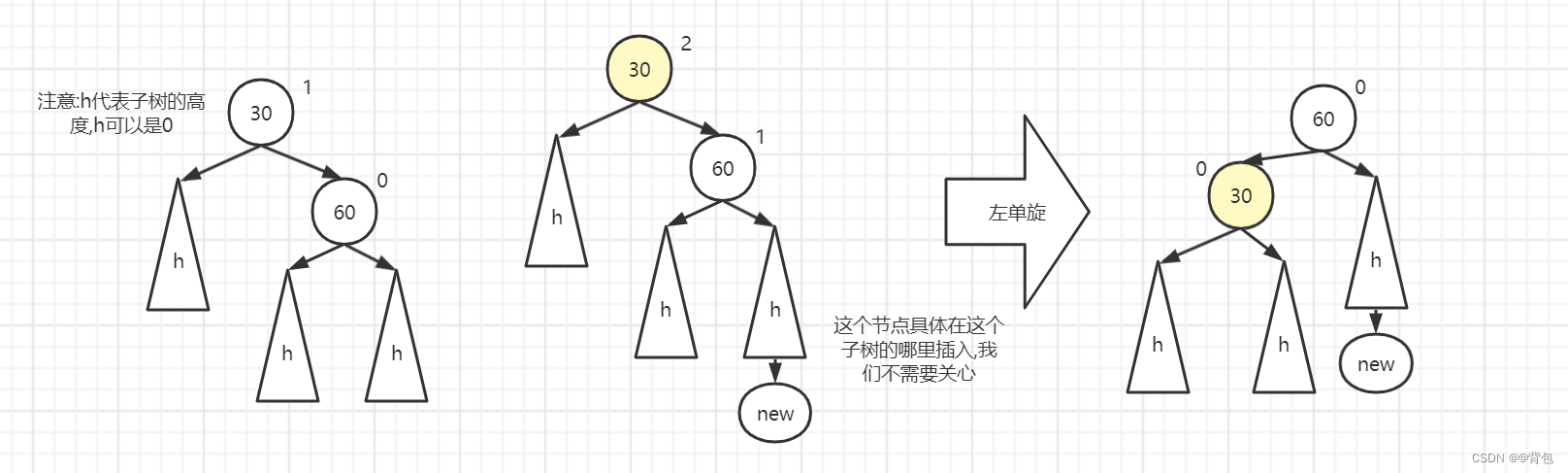
 其实就是把30拿下来,60替代它的位置即可

此时我们要注意,这里我们发现平衡因子异常的点,也就是30这个节点,它不一定是整棵树的根,它有可能只是一个子树的根,但是在旋转过程中,我们不需要关心它上面的结构是什么,我们旋转完成之后,重新链接上去就行了.

给重要的节点标上名字,怎么旋转的,我们就一目了然了,因为是三叉链条,我们直接操作指针即可!

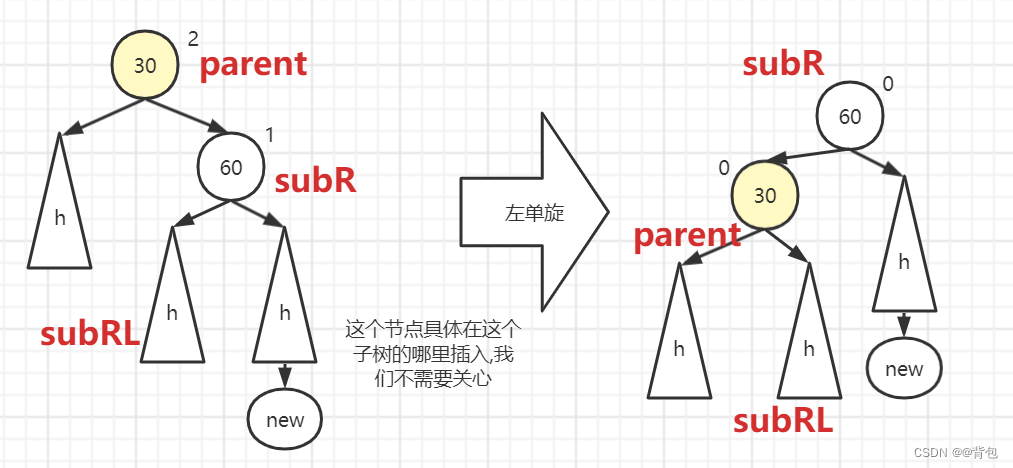
我们把思路转化成代码:

首先,右右触发左单旋,即parent->_bf==2&&cur->_bf==1(在上图中cur是parent的右孩子),这个时候触发左单旋.

if (parent->_bf == 2 && cur->_bf == 1) {
	//注意这里肯定是bf==1的情况 -- 才是单旋
	//parent->_bf==2说明是左单旋
	rotate_left(parent);//旋转就动了6个指针 -- O(1)
}
	void rotate_left(Node* parent) {
		//当然我们还要注意处理parent指针
		//parent和subR不可能为空 -- ，但是subRL可能为空
		//1.parent是整颗树根
		//2.parent是子树的根
		//最后更新一下平衡因子
		//只有subR和parent的平衡因子受到了影响
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL) {
			subRL->_parent = parent;
		}
		Node* ppNode = parent->_parent;//记录一下原先parent的parent
		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent) {
			_root = subR;
			subR->_parent = nullptr;
		}
		else {
			//如果ppNode==nullpt，是不会进来这里的
			if (ppNode->_left == parent) {
				ppNode->_left = subR;
			}
			else {
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}
		//更新一下平衡因子
		subR->_bf = parent->_bf = 0;//这个看图就行了
	}

右单旋:新节点插入较高左子树的左侧

大家注意,这里的触发条件是,较高的是左子树,而且插入的是在该左子树的左侧

这里其实就是左单旋的一个镜像,博主把图画给大家,代码相信我们已经可以自己写出来了

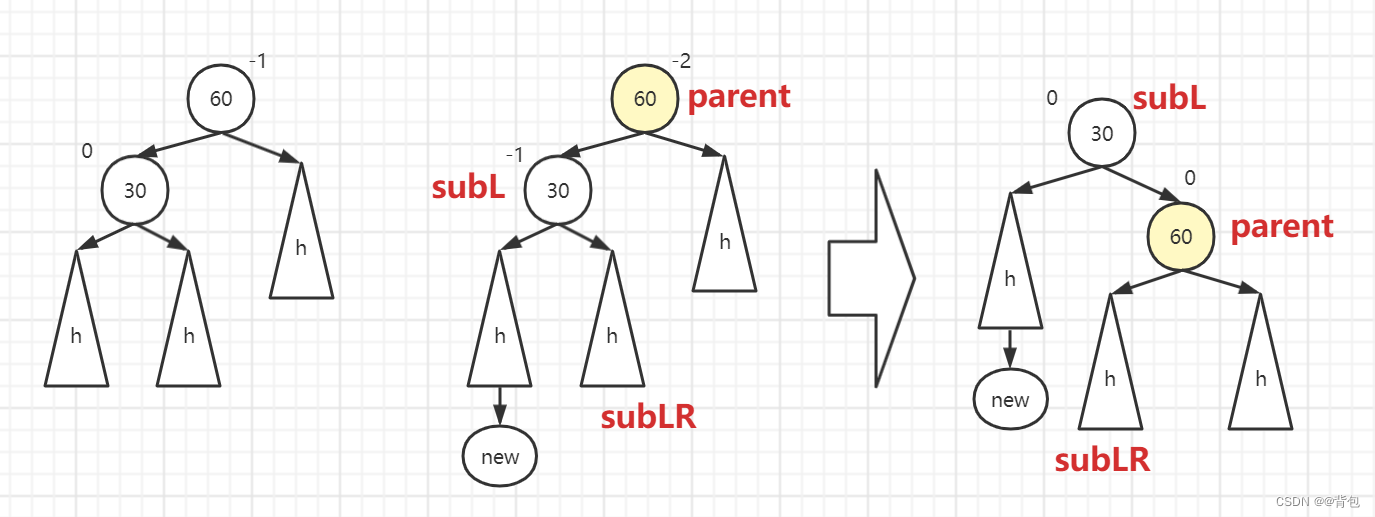
由图片我们可以得知,触发条件时parent->_bf==-2&&cur->_bf==-1

代码如下:

else if (parent->_bf == -2 && cur->_bf == -1) {
    //右单旋
	rotate_right(parent);
}
//右单旋 -- 思路和左单旋是镜像 -- 很简单
	void rotate_right(Node* parent) {
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR) {
			subLR->_parent = parent;
		}
		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;
		if (_root == parent) {
			_root = subL;
			subL->_parent = nullptr;
		}
		else {
			if (ppNode->_left == parent) {
				ppNode->_left = subL;
			}
			else {
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
		//更新平衡因子
		subL->_bf = parent->_bf = 0;
	}

双旋:

看到这里,难道这两种单旋就可以解决所有问题了吗?答案是否定的,我们举个例子:

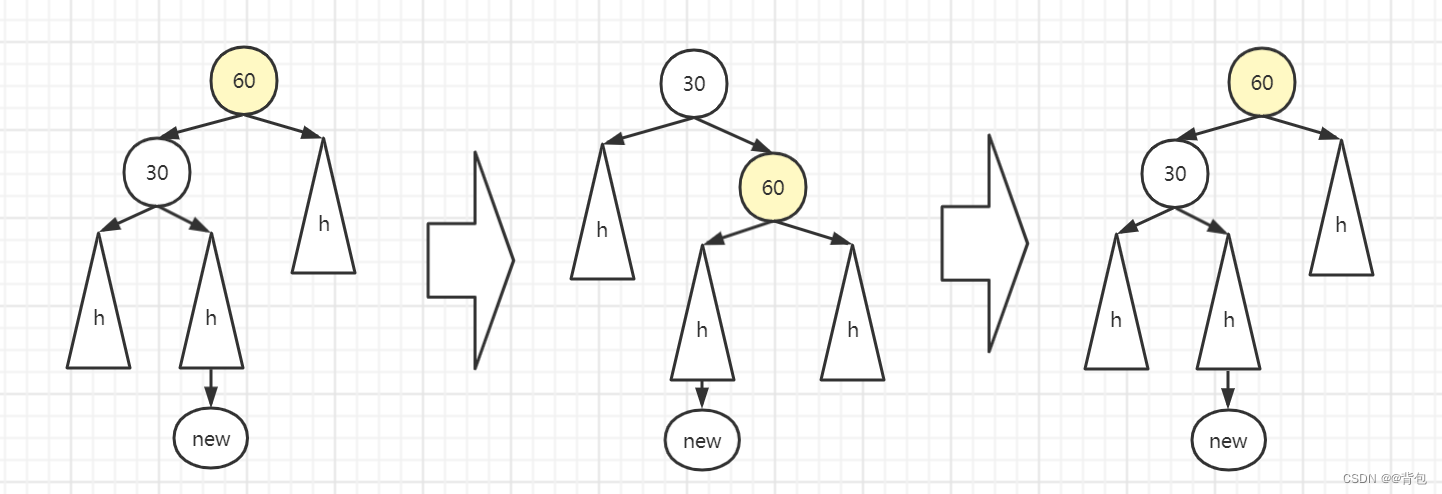
 我们可以看到这种情况,无论怎么单旋,我们都不能使树便平衡.

由此我们引出双旋:

左右双旋:新节点插入较高左子树的右侧:先左旋后右旋

双旋的过程会比单旋的过程复杂一些

其中,左右双旋分别有三种插入的情况,如图所示:

其中情况3:h==0,此时60就是新插入的节点

下面是旋转的过程:

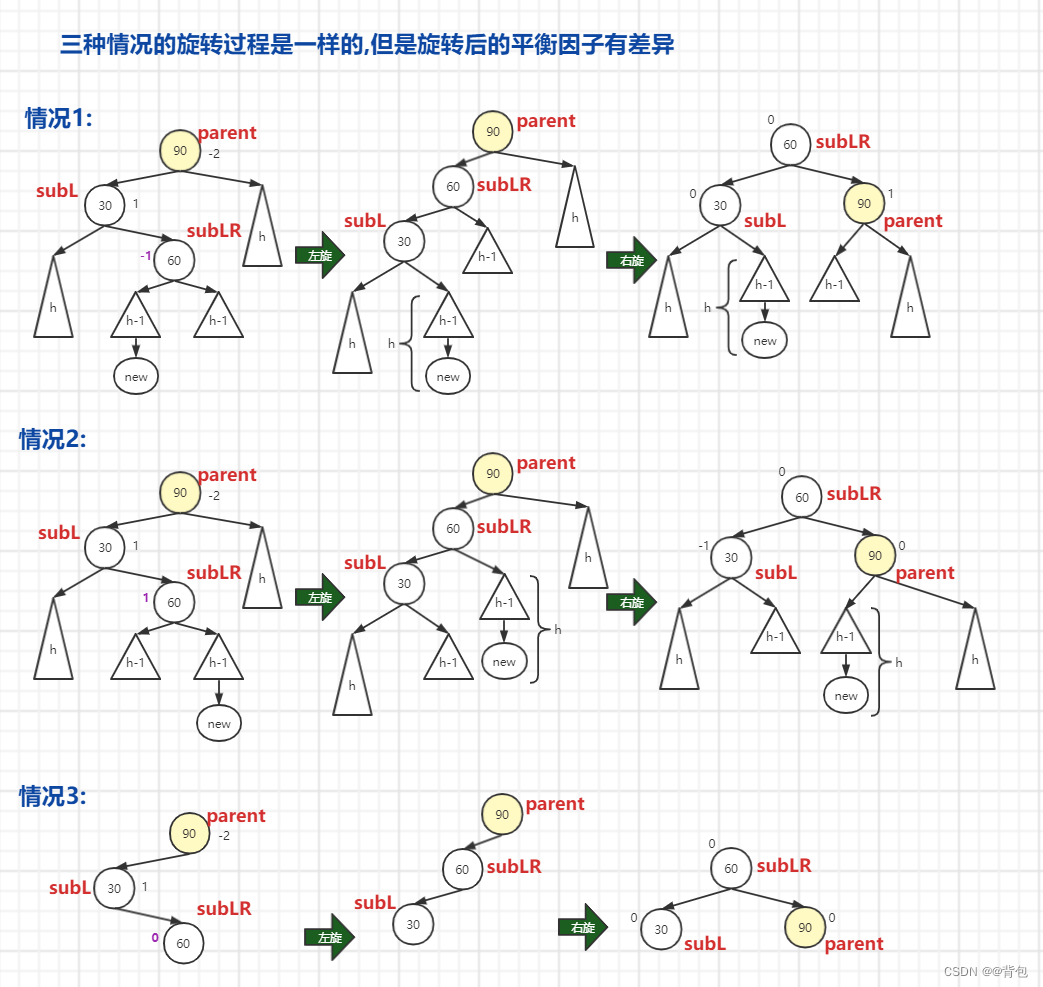
 相信上面的图已经把旋转过程解释得非常清晰了,其实就是两次单旋的组合

现在我们要重点讨论旋转后的平衡因子的更新:

我们可以发现最后的平衡因子取决于初始状态下subLR的平衡因子

情况1: subLR->_bf==-1

  • 旋转后parent,subL,subLR的平衡因子分别为1,0,0

情况2: subLR->_bf==1

  • 旋转后parent,subL,subLR的平衡因子分别为0,-1,0

情况3: subLR->_bf==0

  • 旋转后parent,subL,subLR的平衡因子分别为0,0,0

现在我们只需要对照着图片,对照着调整后的平衡因子,就可以很快的写出代码:

 首先,通过图片我们可以知道,左右双旋的触发条件是:

parent->_bf == -2 && cur->_bf == 1

else if (parent->_bf == -2 && cur->_bf == 1) {
	//左右双旋
	rotate_left_right(parent);
}
    void rotate_left_right(Node* parent) {
		//要在单旋之前记录一下，因为单旋之后平衡因子会变
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;//记录一下subLR的平衡因子
		rotate_left(parent->_left);//先最左边进行一个左旋
		rotate_right(parent);//再对自己进行一个右旋转
		//如何区分三种情况的平衡因子更新呢？

		subLR->_bf = 0;//一定要画图！三种情况的subLR最终都是0
		if (bf == 1) {
			//情况1
			parent->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1) {
			//情况2
			parent->_bf = 1;
			subL->_bf = 0;
		}
		else if (bf == 0) {
			//情况3
			parent->_bf = 0;
			subL->_bf = 0;
		}
		else assert(false);
	}

右左双旋:新节点插入较高右子树的左侧:先右旋后左旋

同样,右左双旋也有三种情况.

右左双旋其实就是左右双旋的一个镜像,搞明白了左右双旋,右左双旋直接画一下图,总结一下三种情况的平衡因子,直接写代码就行了.

触发条件:

parent->_bf == 2 && cur->_bf == -1

else if (parent->_bf == 2 && cur->_bf == -1) {
	//右左双旋
	rotate_right_left(parent);
}
    void rotate_right_left(Node* parent) {
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		rotate_right(parent->_right);
		rotate_left(parent);
		subRL->_bf = 0;
		if (bf == 1) {
			subR->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1) {
			subR->_bf = 1;
			parent->_bf = 0;
		}
		else if (bf == 0) {
			subR->_bf = 0;
			parent->_bf = 0;
		}
		else assert(false);
	}

四、AVL树的检验 

写到这里,我们就可以尝试插入一些节点,检查AVL树是否平衡了

当然,我们可以通过调试,打断点去检查这棵树,但是这样很麻烦.

同时,我们是不能通过检查中序遍历是否有序去判断AVL树的合法性的.因为所有的搜索树中序遍历都是有序的.

我们要通过AVL树的性质去检查,检查每颗子树的左右子树高度差是否小于等于1:

当然现在写出这种代码对于我们来说其实很简单了,这里也提供一道里扣题的传送门,其实就是AVL树的检验,大家可以顺便完成它

面试题 04.04. 检查平衡性icon-default.png?t=M85Bhttps://leetcode.cn/problems/check-balance-lcci/这里博主也一起提供中序遍历的代码:

class AVL {
//...
//...
//...
public:
	void inorder() {
		_inorder(this->_root);
	}
	bool is_balance() {
		return _is_balance(this->_root);
	}
private:
	void _inorder(Node* root) {
		if (root == nullptr) {
			return;
		}
		_inorder(root->_left);
		cout << (root->_kv).first << ":" << (root->_kv).second << endl;
		_inorder(root->_right);
	}
	int _height(Node* root) {
		if (root == nullptr)return 0;
		int leftHT = _height(root->_left);
		int rightHT = _height(root->_right);
		return max(leftHT, rightHT) + 1;
	}
	bool _is_balance(Node* root) {
		if (root == nullptr)return true;
		int leftHT = _height(root->_left);//左子树高度
		int rightHT = _height(root->_right);//右子树高度
		int diff = rightHT - leftHT;
		//把平衡因子也检查一下
		if (diff != root->_bf) {
			cout << root->_kv.first << "的平衡因子异常" << endl;
			return false;
		}
		return abs(diff) < 2
			&& _is_balance(root->_left)//判断一下左子树是否平衡
			&& _is_balance(root->_right);//判断一下右子树是否平衡
	}
}

五、删除等接口

讲到这里有伙伴可能会问,为什么讲AVL,不讲删除那些接口呢?

因为,校招,公司面试,以后工作中都基本不会考察到AVL树的删除接口,红黑树也是一样,我们只需要掌握插入接口就行了.

AVL树,红黑树我们都是做了解性学习,我们并不需要去手撕它的全部代码,这样时间成本很大,意义不大.我们学习AVL树,我们需要深入的去理解它的结构,学习一个插入接口,我们已经可以很好的做到这一点了.

这里博主大概讲一下删除的步骤:

一开始也是像搜索树一样找到要删除的节点,用替换法删除,删除后也是同样,检查平衡性.如果平衡性被破坏,进行旋转,这个过程其实就大概是插入的反方向操作

六、AVL.h整体代码

#pragma once

#include<map>
#include<set>
#include<algorithm>
#include<assert.h>
#include<time.h>
using namespace std;

template<class K,class V>
struct AVLNode {
public:
	AVLNode<K, V>* _left;
	AVLNode<K, V>* _right;
	AVLNode<K, V>* _parent;
	pair<K, V>_kv;
	int _bf;  //balance factor
public:
	AVLNode(const pair<K, V>& kv)
		:_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0) {}
};

//如何更新平衡因子
//如何旋转



template<class K, class V>
struct AVL {
	typedef AVLNode<K, V>Node;
private:
	Node* _root = nullptr;
private:
	//左单旋
	void rotate_left(Node* parent) {
		//当然我们还要注意处理parent指针
		//parent和subR不可能为空 -- ，但是subRL可能为空
		//1.parent是整颗树根
		//2.parent是子树的根
		//最后更新一下平衡因子
		//只有subR和parent的平衡因子受到了影响
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL) {
			subRL->_parent = parent;
		}
		Node* ppNode = parent->_parent;//记录一下原先parent的parent
		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent) {
			_root = subR;
			subR->_parent = nullptr;
		}
		else {
			//如果ppNode==nullpt，是不会进来这里的
			if (ppNode->_left == parent) {
				ppNode->_left = subR;
			}
			else {
				ppNode->_right = subR;
			}
			subR->_parent = ppNode;
		}
		//更新一下平衡因子
		subR->_bf = parent->_bf = 0;//这个看图就行了
	}
	//右单旋
	void rotate_right(Node* parent) {
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR) {
			subLR->_parent = parent;
		}
		Node* ppNode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;
		if (_root == parent) {
			_root = subL;
			subL->_parent = nullptr;
		}
		else {
			if (ppNode->_left == parent) {
				ppNode->_left = subL;
			}
			else {
				ppNode->_right = subL;
			}
			subL->_parent = ppNode;
		}
		//更新平衡因子
		subL->_bf = parent->_bf = 0;
	}
	//左右双旋
	void rotate_left_right(Node* parent) {
		//要在单旋之前记录一下，因为单旋之后平衡因子会变
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;//记录一下subLR的平衡因子
		rotate_left(parent->_left);//先最左边进行一个左旋
		rotate_right(parent);//再对自己进行一个右旋转
		//如何区分三种情况的平衡因子更新呢？

		subLR->_bf = 0;//一定要画图！三种情况的subLR最终都是0
		if (bf == 1) {
			//情况1
			parent->_bf = 0;
			subL->_bf = -1;
		}
		else if (bf == -1) {
			//情况2
			parent->_bf = 1;
			subL->_bf = 0;
		}
		else if (bf == 0) {
			//情况3
			parent->_bf = 0;
			subL->_bf = 0;
		}
		else assert(false);
	}
	//右左双旋
	void rotate_right_left(Node* parent) {
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;
		rotate_right(parent->_right);
		rotate_left(parent);
		subRL->_bf = 0;
		if (bf == 1) {
			subR->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1) {
			subR->_bf = 1;
			parent->_bf = 0;
		}
		else if (bf == 0) {
			subR->_bf = 0;
			parent->_bf = 0;
		}
		else assert(false);
	}
public:
	//我们先不返回pair，到时候我们封装map的时候在搞
	bool insert(const pair<K, V>& kv) {
		if (_root == nullptr) {
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur) {
			if (cur->_kv.first < kv.first) {
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first) {
				parent = cur;
				cur = cur->_left;
			}
			else return false;
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first) {
			parent->_right = cur;
		}
		else  {
			parent->_left = cur;
		}
		cur->_parent = parent;
		//控制平衡
		//先更新平衡因子
		while (parent) {//只有根没有父亲
			//最坏可能需要更新到根
			if (cur == parent->_right) {
				parent->_bf++;
			}
			else {
				parent->_bf--;
			}

			if (parent->_bf == 0) {
				//高度不变 -- 停止更新
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1) {
				//继续更新
				parent = parent->_parent;
				cur = cur->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2) {
				//说明parent所在的子树已经不平衡了 -- 需要旋转
				//左旋
				if (parent->_bf == 2 && cur->_bf == 1) {
					//注意这里肯定是bf==1的情况 -- 才是单旋
					//parent->_bf==2说明是左单旋
					rotate_left(parent);//旋转就动了6个指针 -- O(1)
				}
				else if (parent->_bf == -2 && cur->_bf == -1) {
					rotate_right(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1) {
					//左右双旋
					rotate_left_right(parent);
				}
				else if (parent->_bf == 2 && cur->_bf == -1) {
					//右左双旋
					rotate_right_left(parent);
				}
				else assert(false);
				break;
			}
			else {
				assert(false);//理论上不能走到这里
			}
		}
		return true;
	}
public:
	void inorder() {
		_inorder(this->_root);
	}
	bool is_balance() {
		return _is_balance(this->_root);
	}
private:
	void _inorder(Node* root) {
		if (root == nullptr) {
			return;
		}
		_inorder(root->_left);
		cout << (root->_kv).first << ":" << (root->_kv).second << endl;
		_inorder(root->_right);
	}
	int _height(Node* root) {
		if (root == nullptr)return 0;
		int leftHT = _height(root->_left);
		int rightHT = _height(root->_right);
		return max(leftHT, rightHT) + 1;
	}
	bool _is_balance(Node* root) {
		if (root == nullptr)return true;
		int leftHT = _height(root->_left);//左子树高度
		int rightHT = _height(root->_right);//右子树高度
		int diff = rightHT - leftHT;
		//把平衡因子也检查一下
		if (diff != root->_bf) {
			cout << root->_kv.first << "的平衡因子异常" << endl;
			return false;
		}
		return abs(diff) < 2
			&& _is_balance(root->_left)//判断一下左子树是否平衡
			&& _is_balance(root->_right);//判断一下右子树是否平衡
	}
};

void test1() {
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	AVL<int, int>t1;
	for (auto e : a) {
		t1.insert(make_pair(e, e));
	}
	t1.inorder();
	cout << "is_balance():" << t1.is_balance() << endl;
}
void test2(){
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	AVL<int, int>t1;
	for (auto e : a) {
		t1.insert(make_pair(e, e));
	}
	t1.inorder();
	cout << "is_balance():" << t1.is_balance() << endl;
}
void test3(){
	size_t N = 10000;
	srand(time(nullptr));
	AVL<int, int>t1;
	for (size_t i = 0; i < N; ++i) {
		int x = rand();
		t1.insert(make_pair(x, i));
	}
	cout << "is_balance():" << t1.is_balance() << endl;
}

七、总结

看到这里,大家应该对AVL树的实现,重点是它的旋转有了比较深入的了解了。这篇博客博主花了很多心思在画图上，也投入了很多时间到画图上。下期给大家带来红黑树的内容。希望大家可以多多支持，一键三连，点赞关注收藏评论后在离开哦!

( 转载时请注明作者和出处。未经许可，请勿用于商业用途 )
更多文章请访问我的主页

@背包https://blog.csdn.net/Yu_Cblog?type=blog

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/3445.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

计算机毕业设计（附源码）python职业高中智慧教学系统

计算机毕业设计（附源码）python职业高中智慧教学系统

项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等等。 环境需要 1.运行环境&#xff1a;最好是python3.7.7&#xff0c;我…
阅读更多...
ASCII纯文本绘制流程图

ASCII纯文本绘制流程图

我们使用纯文本写代码&#xff0c;有了Markdown又可以使用纯文本写文档&#xff0c;那么图片&#xff0c;能不能使用纯文本描述呢&#xff1f; Text Flow是什么&#xff1f; Text Flow&#xff1a;一个强大的在线ASCII流程图绘制工具&#xff0c;是程序员大佬们很喜爱的制作流…
阅读更多...
【AI绘图】咒术师的评级指南

【AI绘图】咒术师的评级指南

成为咒术师之路 python版本要选用3.9.7 C盘或系统缓存目录预留5G空间 咒术师评级 以下内容仅供参考。。 三级咒术师 理解咒言的使用&#xff0c;正向咒言&#xff0c;逆向咒言&#xff0c;构图要素的表达 二级咒术师 能够对咒物做后期调整&#xff0c;校正手部 一级咒术师…
阅读更多...
Redis

Redis

1.概念:redis是一款高性能的NOSQL系列的非关系型数据库 关系型数据库&#xff1a;数据之间有关联关系&#xff0c;数据存储在硬盘的文件上 非关系型数据库&#xff1a;数据之间没有关联关系&#xff0c;数据存储在内存中 是一款用C语言开发…
阅读更多...
猿创征文｜一文吃透JAVA初学者的开发工具

猿创征文｜一文吃透JAVA初学者的开发工具

✅作者简介&#xff1a;热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;乐趣国学的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏&#xff1a;CSDN活动专…
阅读更多...
【算法】网络最大流问题，三次尝试以失败告终

【算法】网络最大流问题，三次尝试以失败告终

文章目录开始基本思路&#xff1a;“反悔”机制干活尝试一&#xff1a;深度优先搜索尝试二&#xff1a;少走弯路尝试三&#xff1a;最短增广路径&#xff0c;广度优先还是没ac记两个小bug1. 数组越界2. 写错变量名小结最后一个版本的代码&#xff08;C&#xff09;定义类与函数…
阅读更多...
谷雨妹子要出国

谷雨妹子要出国

文 / 谷雨&#xff08;微信公众号&#xff1a;王不留&#xff09; 作为出差在外的实施团队中的唯一一位女生&#xff0c;我可以独享一个单间&#xff0c;晚上的备考时候不会受影响&#xff0c;心里倒有点美嗞嗞的。 目前工作状态是 996&#xff08;早上九点到晚上九点&#xf…
阅读更多...
常用短信平台一览，记得收藏哦

常用短信平台一览，记得收藏哦

市面上的短信平台很杂很多&#xff0c;小到几个人的公司、大到腾讯、阿里这样的巨无霸都在做&#xff0c;但常用的就那么几个&#xff0c;因而用户的选择也存在不少的困惑。 在我看来&#xff0c;我觉得选择短信平台、在我看来有这几个需要的注意地方&#xff1a; 1、价格 无论…
阅读更多...
Java：Session 会话详解

Java：Session 会话详解

在介绍本篇的主角之前, 我们先复习一下 Cookie 为了实现在游览器的持久性存储和安全性考虑, 游览器提供了一个机制—— Cookie , Cookie 的储存空间很有限, 不同的游览器Cookie空间上限也不同, 一般总上限是 4k 个字节左右 (例如 Firefox), 其储存也只是按照域名进行分块存储, …
阅读更多...
在众多编程语言中,我为什么要学Python?

在众多编程语言中,我为什么要学Python?

前言 编程语言排行榜三剑客Java、C、C&#xff0c;长期统治榜首&#xff0c;今日python重回榜首 &#xff08;文末送福利&#xff09; python的前世今生 1、最新动态 TIOBE排行榜是根据互联网上有经验的程序员、课程和第三方厂商的数量&#xff0c;并使用搜索引擎&#xff…
阅读更多...
【算法篇-动态规划】手撕各大背包问题 —— 01背包

【算法篇-动态规划】手撕各大背包问题 —— 01背包

背包问题1. 最基础的背包 —— 01背包 &#xff08;必看&#xff09;1.1 分析1.2 状态转移方程 和 边界条件1.3 代码1.3.1 代码模拟1.4 空间复杂度的优化1.4.1 错误的优化方式1.4.2 正确的优化方式1.5 终极版优化总结本文章参考自 B站 董晓算法 董晓算法 1. 最基础的背包 ——…
阅读更多...
Linux下git和gdb的使用

Linux下git和gdb的使用

&#x1f680;每日鸡汤&#xff1a;生活不相信眼泪&#xff0c;即使你把眼泪流成珍珠&#xff0c;灰暗的生活也不会因此而闪光。 目录 一、使用git命令行 1.1安装git、配置仓库 Ⅰ.gitignore Ⅱ.git 1.2git的基本使用 二、Linux调试器-gdb 2.1、gdb的使用 2.2、 debug与…
阅读更多...
矩阵求导简记

矩阵求导简记

很多机器学习算法都需要求解最值&#xff0c;比如最小二乘法求解样本空间相对拟合曲线的最短距离&#xff0c;最值的求解往往通过求导来计算&#xff0c;而机器学习中又常用矩阵来处理数据&#xff0c;所以很多时候会涉及到矩阵的求导。矩阵求导就像是线性代数和微积分的结合&a…
阅读更多...
熬夜肝出囊括Java后端95%的面试题解析

熬夜肝出囊括Java后端95%的面试题解析

为大家整理了一版java高频面试题&#xff0c;其实&#xff0c;一直有大佬在面试&#xff0c;不是在面试&#xff0c;就是在面试的路上&#xff0c;2022其实不是个适合跳槽的年份&#xff0c;稳稳当当当然好&#xff0c;但是&#xff0c;也别委屈自己呀&#xff0c;话不多说&…
阅读更多...
Kotlin编程实战——与Java互操作(10)

Kotlin编程实战——与Java互操作(10)

一 概述 Kotlin 中调用 Java 代码Java 中调用 Kotlin 二 Kotlin 中调用 Java 代码 Getter 和 Setter返回 void 的方法将 Kotlin 中是关键字的 Java 标识符进行转义空安全与平台类型Java类型映射kotlin类型Kotlin 中的 Java 泛型Java 可变参数 三 Java 中调用 Kotlin 属性实…
阅读更多...
【ELM预测】基于matlab探路者算法优化极限学习机预测（含前后对比）【含Matlab源码 2204期】

【ELM预测】基于matlab探路者算法优化极限学习机预测（含前后对比）【含Matlab源码 2204期】

一、探路者算法简介 提出的一种新兴的智能优化算法&#xff0c;该算法的思想起源于群体动物的狩猎行为&#xff0c;种群中的个体分为探路者和跟随者两种角色。算法的寻优过程模拟了种群寻找食物的探索过程&#xff0c;利用探路者、跟随者两种角色不同的位置更新方式以及角色间…
阅读更多...
NR/5G - PUSCH repetition次数

NR/5G - PUSCH repetition次数

--- R15 DCI format 0-1 PUSCH 38.214中的描述&#xff0c;DCI format 0-1调度的PUSCH&#xff0c;包括C-RNTI/MCS-C-RNTI动态DCI调度PUSCH以及CS-RNTI&#xff0c;NDI1时候指示的Configured Grant的重传调度PUSCH&#xff0c;通过PUSCH-Config中的pusch-AggregationFactor指示…
阅读更多...
谷粒学院——Day02【环境搭建和讲师管理接口开发】

谷粒学院——Day02【环境搭建和讲师管理接口开发】

前后端分离概念 传统单体结构 前后端分离结构 前后端分离就是将一个单体应用拆分成两个独立的应用&#xff1a;前端应用和后端应用&#xff0c;以JSON格式进行数据交互。 后台讲师管理模块环境搭建 一、数据库设计 数据库 guli_edu 数据库 guli_edu.sql # # Structure fo…
阅读更多...
3.1 Python 字符串类型常用操作及内置方法

3.1 Python 字符串类型常用操作及内置方法

文章目录1. 类型转换2. 字符串索引取值3. 遍历字符串4. 统计长度5. 字符串的复制与拼接5.1 字符串的复制5.2 加号拼接5.3 .join 方法拼接字符串6. 字符比较7. 成员运算8. .format9. .split10. .strip11 . .upper 与 .lower12. .isupper 与 .islower13. .startswith 与 .endswit…
阅读更多...
15 个机器学习的基本 Python 库

15 个机器学习的基本 Python 库

一定有很多次你试图在 Python 中找到一个库来帮助你完成机器学习项目。但是&#xff0c;经常遇到一件事&#xff01;今天有如此多的 Python 库可用&#xff0c;并且许多库在每几年之后都会大量发布&#xff0c;因此选择合适的库并不容易。 有时会花费数小时寻找合适的库&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023