统计一个圆中点的数目
难度:中等
给你一个数组 points ,其中 points[i] = [xi, yi] ,表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。
同时给你一个数组 queries ,其中 queries[j] = [xj, yj, rj] ,表示一个圆心在 (xj, yj) 且半径为 rj 的圆。
对于每一个查询 queries[j] ,计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ,我们同样认为它在圆 内 。
请你返回一个数组 answer ,其中 answer[j] 是第 j 个查询的答案。
示例 1:
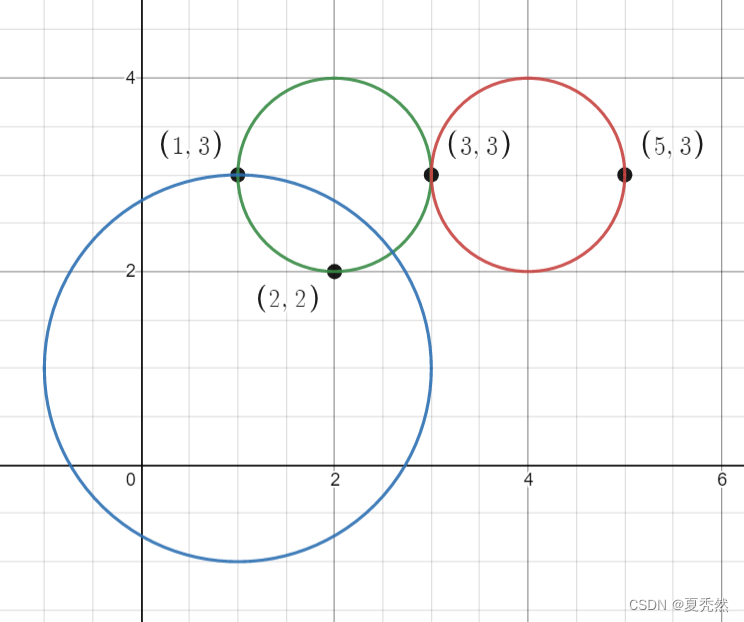
输入:points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出:[3,2,2]
解释:所有的点和圆如上图所示。
queries[0] 是绿色的圆,queries[1] 是红色的圆,queries[2] 是蓝色的圆。
示例 2:
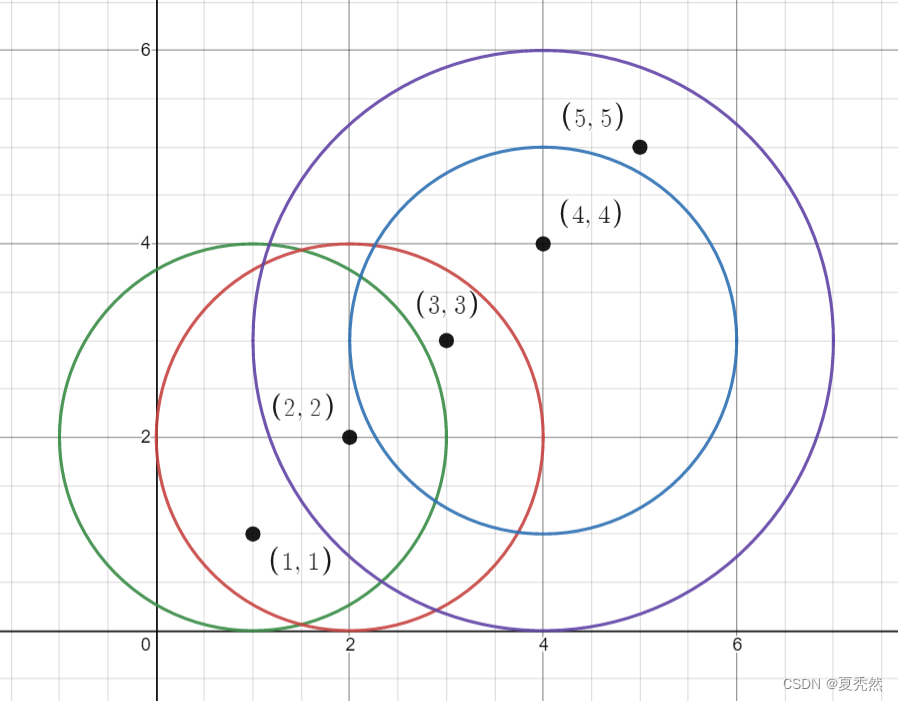
输入:points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出:[2,3,2,4]
解释:所有的点和圆如上图所示。
queries[0] 是绿色的圆,queries[1] 是红色的圆,queries[2] 是蓝色的圆,queries[3] 是紫色的圆。
枚举每个点是否在每个圆中
思路:
我们可以使用二重循环,对于每一个查询,枚举所有的点,依次判断它们是否在查询的圆中即可。
如果查询圆的圆心为 ( c x , c y ) (c_x, c_y) (cx,cy),半径为 c r c_r cr,枚举的点坐标为 ( p x , p y ) (p_x, p_y) (px,py),那么点在圆中(包括在圆上的情况)当且仅当点到圆心的距离小于等于半径。我们可以用以下方法进行判断:
( c x − p x ) 2 + ( c y − p y ) 2 ≤ c r 2 (c_x-p_x)^2 + (c_y-p_y)^2 \leq c_r^2 (cx−px)2+(cy−py)2≤cr2
注意这里两侧的距离都进行了平方操作,这样可以避免引入浮点数,产生不必要的误差。
复杂度分析:
- 时间复杂度: O ( m n ) O(mn) O(mn),其中 m m m 和 n n n 分别是数组 points \textit{points} points 和 queries \textit{queries} queries 的长度。
- 空间复杂度: O ( 1 ) O(1) O(1)。
class Solution:
def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:
res = []
for i in queries:
count = 0
for j in points:
if pow((i[0] - j[0]) ** 2 + (i[1] - j[1]) ** 2, 1/2) <= i[2]:
count += 1
res.append(count)
return res
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/queries-on-number-of-points-inside-a-circle