引言:2021年用Transformer实现视频超分VSR的文章,改进了SA并在FFN中加入了光流引导
论文:【here】
代码:【here】
Video Super-Resolution Transformer
引言
视频超分中有一组待超分的图片,因此视频超分也经常被看做是一个序列问题。这种序列问题的解决方法通常有RNN,SLTM,和transformer。由于transformer并不需要递归也更适合,并备受关注
注意力机制
目前用transformer处理图片的思路是全连接注意力机制,the fully connected self-attention(FCSA)
(这里的这个FCSA的概念是作者提出来的,作者举例VIT和PIT都是FCSA,因此我把它当做对整个图像的分成的块做自注意力)
然而,作者认为这样的FCSA的机制并不能很好的提取空间局部信息,但是局部信息对于VSR来说又是很关键的。
此外,除了空间局部信息,时域信息也是很重要的,视频中的图片中的信息可以通过相邻的图片进行补充。现在,该如何用transformer来处理时域信息也是没有被探索过的(这个领域还没有人做)
前馈网络
现有的前馈网络token-wise feed-forward layer不能实现图像之间的对齐,这里强调token,即是指全连接都是在每一个token中实现的,token和token之间没有关联。token 之间的特征关联在FCSA模块中实现的,但是在FFN中没有特征传播。因此,在这个模块中,作者实现了以像元为单位(而不是token),实现了特征传播和特征对齐
问题定义
第一个定义是映射函数的loss
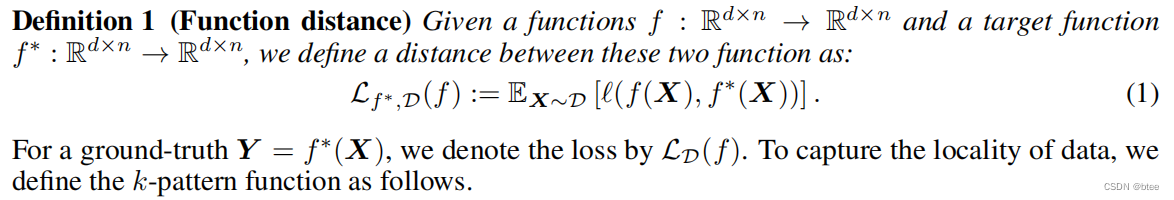
第二个定义是神经元组成/参数传播的定义,同时这个连接了不同神经元的映射与真实映射之间的loss应该小于一个epsilon

第三个定义为视频超分的定义和目标

第四个定义为transformer的架构

(这一块有点枯燥,主要是作者的第二个定义,神经元的参数传播为后面的公式推导奠定基础)
视频超分 Transformer
作者介绍了这样一个公式,来证明FCSA不太适合视频超分tranformer(公式没有看懂,我这里就跳过了)

总之,作者通过这个公式论证了全连接注意力机制FCSA会导致梯度消失的问题
When q is not sufficiently large, the fully connected attention layer may result in the gradient vanishing issue. It implies that the gradient descent will be “stuck” upon the initialization, and thus will fail to learn the k-pattern function. Therefore, the fully connected self-attention layer cannot use the spatial information of each frame since the local information is not encoded in the embeddings of all tokens. Moreover, this issue may become more serious when directly using such layers in video super-resolution.
而如果用作者提出的,则时空卷积自注意力机制STCSA很好的解决了这个问题

STCSA的实现
即将图片划成8 * 8 * 5的小块(这里的5是指连续的图片数),在8 * 8 * 5的3D块中实现块中的像元单位的特征自注意力
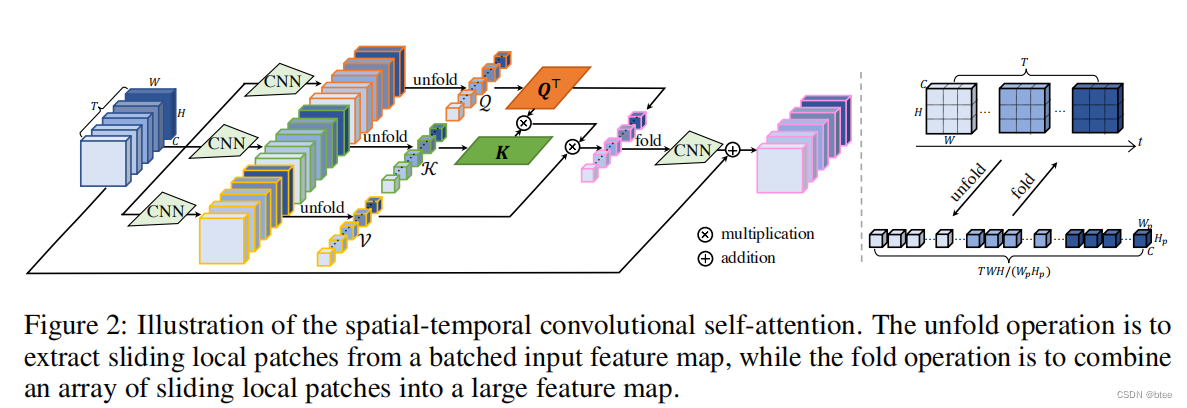
同时,作者还加入了一个3D位置编码信息,编码规则如下

代码(作者非常贴心的加上了尺寸的注释)
class globalAttention(nn.Module):
def __init__(self, num_feat=64, patch_size=8, heads=1):
super(globalAttention, self).__init__()
self.heads = heads
self.dim = patch_size ** 2 * num_feat
self.hidden_dim = self.dim // heads
self.num_patch = (64 // patch_size) ** 2
self.to_q = nn.Conv2d(in_channels=num_feat, out_channels=num_feat, kernel_size=3, padding=1, groups=num_feat)
self.to_k = nn.Conv2d(in_channels=num_feat, out_channels=num_feat, kernel_size=3, padding=1, groups=num_feat)
self.to_v = nn.Conv2d(in_channels=num_feat, out_channels=num_feat, kernel_size=3, padding=1)
self.conv = nn.Conv2d(in_channels=num_feat, out_channels=num_feat, kernel_size=3, padding=1)
self.feat2patch = torch.nn.Unfold(kernel_size=patch_size, padding=0, stride=patch_size)
self.patch2feat = torch.nn.Fold(output_size=(64, 64), kernel_size=patch_size, padding=0, stride=patch_size)
def forward(self, x):
b, t, c, h, w = x.shape # B, 5, 64, 64, 64
H, D = self.heads, self.dim
n, d = self.num_patch, self.hidden_dim
q = self.to_q(x.view(-1, c, h, w)) # [B*5, 64, 64, 64]
k = self.to_k(x.view(-1, c, h, w)) # [B*5, 64, 64, 64]
v = self.to_v(x.view(-1, c, h, w)) # [B*5, 64, 64, 64]
unfold_q = self.feat2patch(q) # [B*5, 8*8*64, 8*8]
unfold_k = self.feat2patch(k) # [B*5, 8*8*64, 8*8]
unfold_v = self.feat2patch(v) # [B*5, 8*8*64, 8*8]
unfold_q = unfold_q.view(b, t, H, d, n) # [B, 5, H, 8*8*64/H, 8*8]
unfold_k = unfold_k.view(b, t, H, d, n) # [B, 5, H, 8*8*64/H, 8*8]
unfold_v = unfold_v.view(b, t, H, d, n) # [B, 5, H, 8*8*64/H, 8*8]
unfold_q = unfold_q.permute(0,2,3,1,4).contiguous() # [B, H, 8*8*64/H, 5, 8*8]
unfold_k = unfold_k.permute(0,2,3,1,4).contiguous() # [B, H, 8*8*64/H, 5, 8*8]
unfold_v = unfold_v.permute(0,2,3,1,4).contiguous() # [B, H, 8*8*64/H, 5, 8*8]
unfold_q = unfold_q.view(b, H, d, t*n) # [B, H, 8*8*64/H, 5*8*8]
unfold_k = unfold_k.view(b, H, d, t*n) # [B, H, 8*8*64/H, 5*8*8]
unfold_v = unfold_v.view(b, H, d, t*n) # [B, H, 8*8*64/H, 5*8*8]
attn = torch.matmul(unfold_q.transpose(2,3), unfold_k) # [B, H, 5*8*8, 5*8*8]
attn = attn * (d ** (-0.5)) # [B, H, 5*8*8, 5*8*8]
attn = F.softmax(attn, dim=-1) # [B, H, 5*8*8, 5*8*8]
attn_x = torch.matmul(attn, unfold_v.transpose(2,3)) # [B, H, 5*8*8, 8*8*64/H]
attn_x = attn_x.view(b, H, t, n, d) # [B, H, 5, 8*8, 8*8*64/H]
attn_x = attn_x.permute(0, 2, 1, 4, 3).contiguous() # [B, 5, H, 8*8*64/H, 8*8]
attn_x = attn_x.view(b*t, D, n) # [B*5, 8*8*64, 8*8]
feat = self.patch2feat(attn_x) # [B*5, 64, 64, 64]
out = self.conv(feat).view(x.shape) # [B, 5, 64, 64, 64]
out += x # [B, 5, 64, 64, 64]
return out
这样就完全考虑8 * 8感受野内的局部特征了,但是块与块之间的边缘只能朝一个方向进行特征传播
于是作者提出了一种新型的FFN
feed-forward Network实现
作者首先将5张图片中的相邻光流求出来,如果边缘图像的另一边没有图了,则跟自己作光流
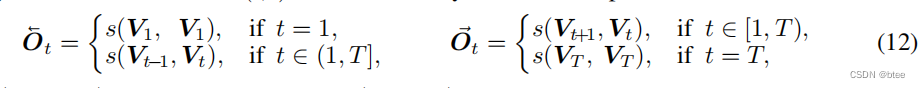
这样可以得到5 * 2张光流图(这里的5指视频图片数),每张图片都有它的前向流图和后向流图,然后前向warp和后向warp后,原有的每张图的时间位置上都可以多加两张图,分别来自前一时刻图片前向warp得到,和后一时刻的图片后向warp得到
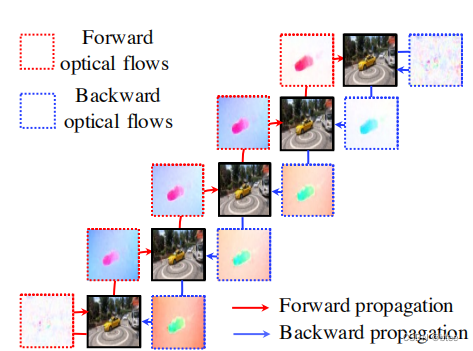
然后通过两组图片的融合,即生成了最终结果
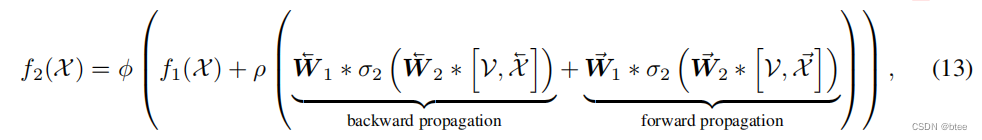
值得一提的是,这里的FFN和传统FFN不同,由于前面的SA部分保留的图片的原有尺寸,这里的FFN直接用3*3卷积实现
class FeedForward(nn.Module):
def __init__(self, num_feat):
super().__init__()
self.backward_resblocks = ResidualBlocksWithInputConv(num_feat+3, num_feat, num_blocks=30)
self.forward_resblocks = ResidualBlocksWithInputConv(num_feat+3, num_feat, num_blocks=30)
self.fusion = nn.Conv2d(num_feat*2, num_feat, 1, 1, 0, bias=True)
self.lrelu = nn.LeakyReLU(negative_slope=0.1, inplace=True)
def forward(self, x, lrs=None, flows=None):
b, t, c, h, w = x.shape
x1 = torch.cat([x[:, 1:, :, :, :], x[:, -1, :, :, :].unsqueeze(1)], dim=1) # [B, 5, 64, 64, 64]
flow1 = flows[1].contiguous().view(-1, 2, h, w).permute(0, 2, 3, 1) # [B*5, 64, 64, 2]
x1 = flow_warp(x1.view(-1, c, h, w), flow1) # [B*5, 64, 64, 64]
x1 = torch.cat([lrs.view(b*t, -1, h, w), x1], dim=1) # [B*5, 67, 64, 64]
x1 = self.backward_resblocks(x1) # [B*5, 64, 64, 64]
x2 = torch.cat([x[:, 0, :, :, :].unsqueeze(1), x[:, :-1, :, :, :]], dim=1) # [B, 5, 64, 64, 64]
flow2 = flows[0].contiguous().view(-1, 2, h, w).permute(0, 2, 3, 1) # [B*5, 64, 64, 2]
x2 = flow_warp(x2.view(-1, c, h, w), flow2) # [B*5, 64, 64, 64]
x2 = torch.cat([lrs.view(b*t, -1, h, w), x2], dim=1) # [B*5, 67, 64, 64]
x2 = self.forward_resblocks(x2) # [B*5, 64, 64, 64]
# fusion the backward and forward features
out = torch.cat([x1, x2], dim=1) # [B*5, 128, 64, 64]
out = self.lrelu(self.fusion(out)) # [B*5, 64, 64, 64]
out = out.view(x.shape) # [B, 5, 64, 64, 64]
return out
实验
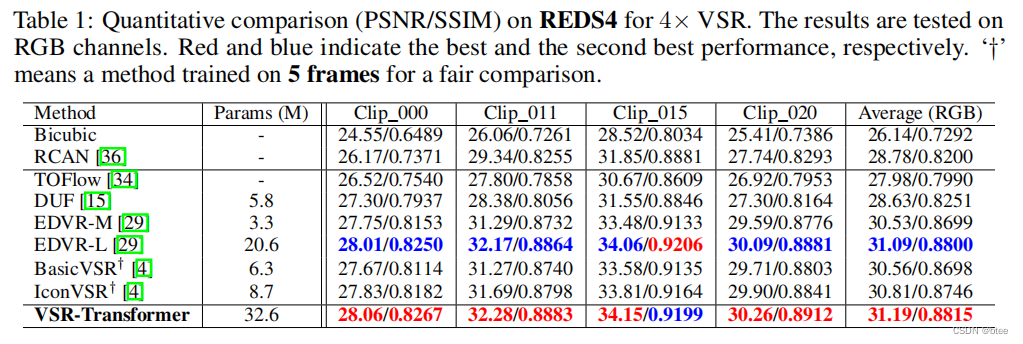

在别的文章里有看到块与块之间会出现伪影,然而文章的结果挺完美的
总结
用transformer解决VSR的问题,虽然在空间小范围内进行attention是可行的,也不会造成太大的计算量,但是总觉得对于transformer的优势没有发挥出来,大的感受野和全局信息的利用才是transformer的优势所在