模型选择

• 训练数据集：训练模型参数
• 验证数据集：选择模型超参数（学习率、批量大小、隐藏大小）
• 非大数据集上通常使用K-折交叉验证
  通过K折平均误差来判断一个参数的好坏，对每一个超参数都会得到一个交叉验证的平均精度，将最好的精度选出来，作为我们采用的超参数

训练误差和泛化误差

• 训练误差：模型在训练数据上的误差
• 泛化误差：模型在新数据上的误差

验证数据集和测试数据集

• 验证数据集：一个用来评估模型好坏的数据集（不要和训练数据集混在一起，例如拿出50%的训练数据）
• 测试数据集：只用一次的数据集

K-则交叉验证（没有足够多数据时使用）

算法：

将训练数据分割成K块
For i=1, ..., K
	使用第i块作为验证数据集，其余的作为训练数据集
报告K各验证集误差的平均

常用：K=5或10

过拟合和欠拟合

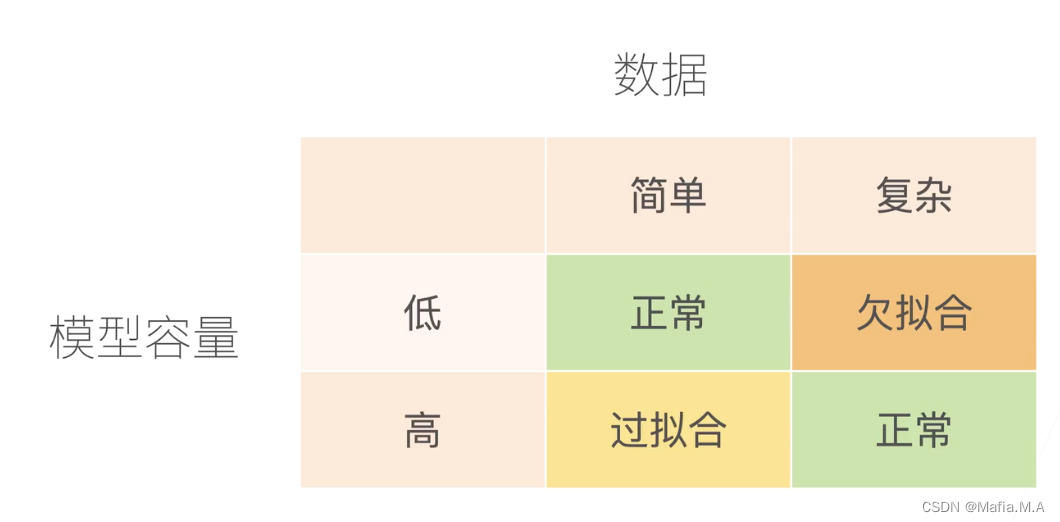
模型容量低——模型简单
模型容量高——模型复杂

模型容量

• 模型容量指的是拟合各种函数的能力
• 低容量的模型难以拟合训练数据
• 高容量的模型可以记住所有的训练数据

模型容量的影响

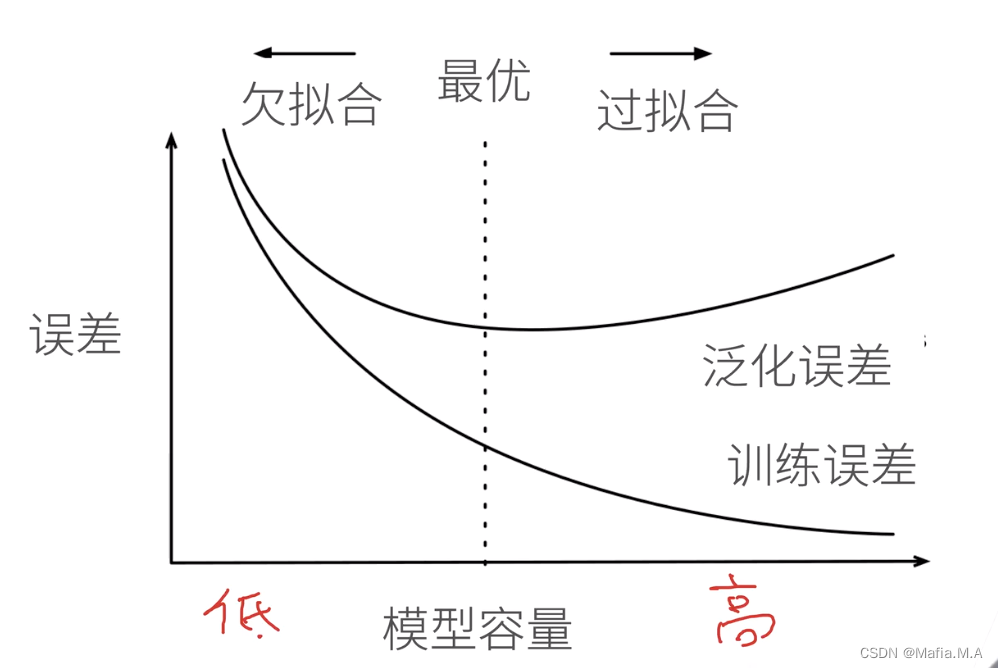
估计模型容量

• 难以在不同的种类算法之间比较（例如树模型和神经网络）
• 给定一个模型种类，将有两个主要因素：参数的个数；参数值的选择范围。
  

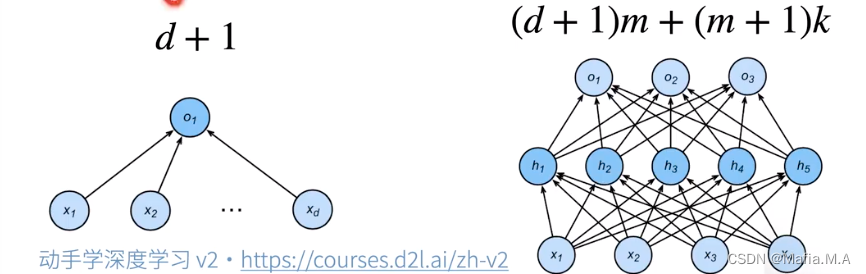
控制模型容量

使用均方范数作为硬性限制

• 通过限制参数值的选择范围来控制模型容量
  

• 冗长不限制偏移b（限不限制都差不多）

• 小的 意味着更强的正则项

数据复杂度

多个重要因素：

• 样本个数
• 每个样本的元素个数
• 时间、空间结构
• 多样性

处理过拟合的方法（1）：权重衰退

一般来说，不会直接使用“均方范数作为硬性限制”优化函数，因为它优化起来相对麻烦一些。

常用均方范数作为柔性限制
对每个θ，都可以找到λ使得之前的目标函数等价于下面

• 可以通过拉格朗日乘子来证明
  

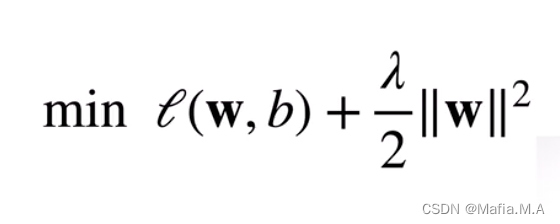
超参数λ控制了正则项的重要程度

• λ = 0 ： 无作用
• λ->∞ ， w* -> 0

如果想把模型复杂度控制地比较低，可以通过增加λ来满足，此时λ不再是一个硬性的限制（所有的值都小于某个值），变成了柔性的限制（更平滑）

参数更新法则

• 权重衰退通过L2正则项使得模型参数不会过大，从而控制模型复杂度
• 正则项权重是控制模型复杂度的超参数

处理过拟合的方法（2）：丢弃法

效果可能会比权重衰退更好。
动机：

1. 一个好的模型需要对输入数据的扰动鲁棒

• 使用有噪音的数据等价于Tikhonov正则（加入数据的噪音，之前是固定噪音，现在是随机噪音，不断地随机加噪音）
• 丢弃法：在层之间加入噪音（丢弃法，不在输入加噪音，在层之间加入噪音，其实是一个正则的）

无偏差的加入噪音

假设 x 是一层到下一层的输出，我们对x加入噪音得到 x’，虽然加入了噪音但我们希望加入的噪音不改变期望E

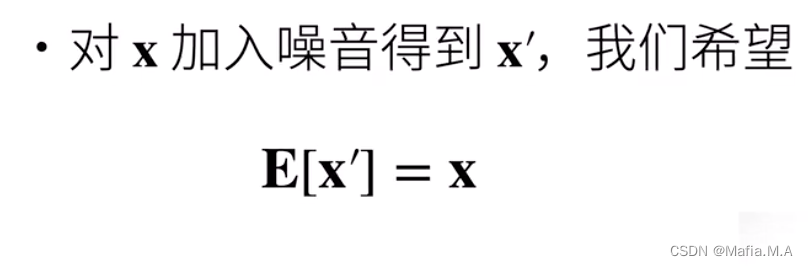
计算$x_i^{\prime }$的期望，仍然与$x$的期望相同，没有产生变化
$E[x_i^{\prime }]=p\ast 0+(1-p)x_i/(1-p)=x_i$

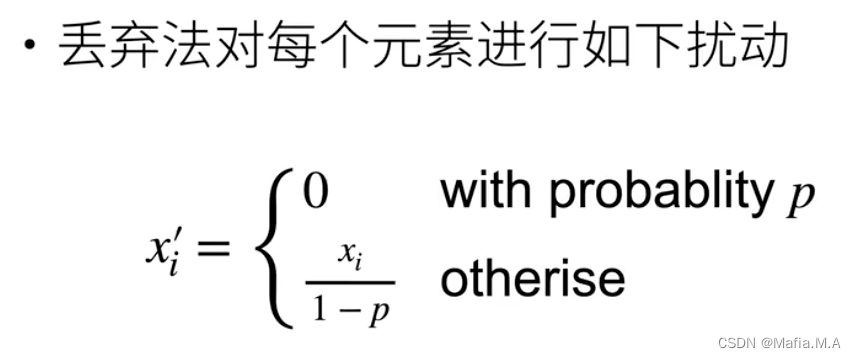
使用丢弃法

drop out使用的地方：通常将丢弃法作用在隐藏全连接层的输出上。

• 假设有第一层（第一个隐藏层）：输入$x$✖️权重$W_1$➕偏移$b_1$，再将其加上激活函数后，得到$h$就是第一个隐藏层的输出；
• 对于第一个隐藏层，使用drop out，将h中间每一个元素作用dropout，使p趋近于0（p为超参数）
  
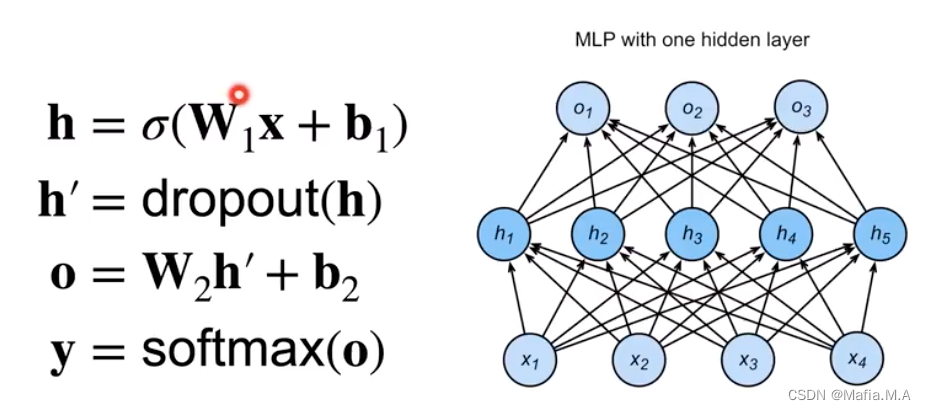
• 第二层，拿到的输入是把前面一层输出的一些元素变成0（如$h_2$、$h_5$变成零）的结果（随机挑选神经元扔出窗外）
  

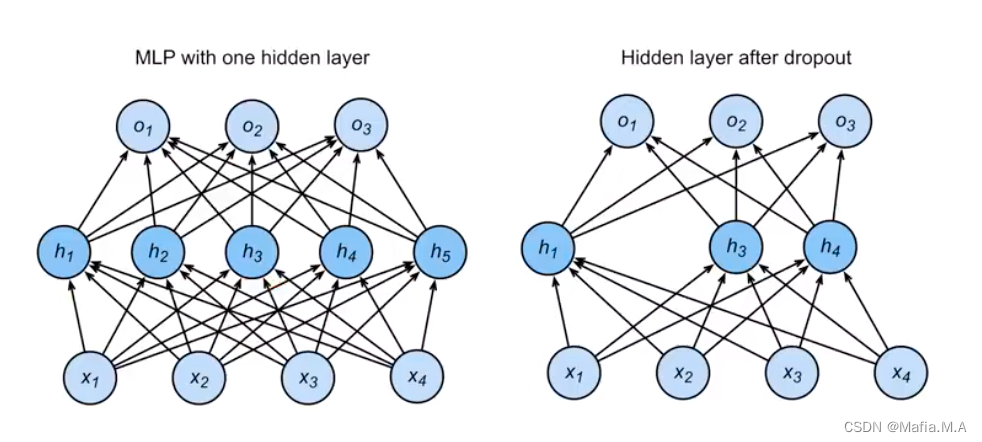
推理（预测）中的丢弃法

正则项只在训练中使用：他们影响模型参数的更新
在推理过程中，丢弃法直接返回输入
$h=dropout(h)$
这样也能保证确定性的输出。

总结：在训练中使用dropout，而在推理（预测过程）中不使用dropout。因为dropout是一个正则项，正则项只在训练中使用，因为它只会对权重产生影响；当我们在预测的时候，权重不需要发生变化，此时不需要正则，在推理中dropout输出的是它本身（对数据没有任何操作）

总结

• 丢弃法将一些输出项随机置0来控制模型复杂度
• 常作用在多层感知机的隐藏层输出上
• 丢弃概率是控制模型复杂度的超参数（如果p=1，就是全部丢掉；p=0，就是没有被丢弃；一般取0.9、0.5、0.1）