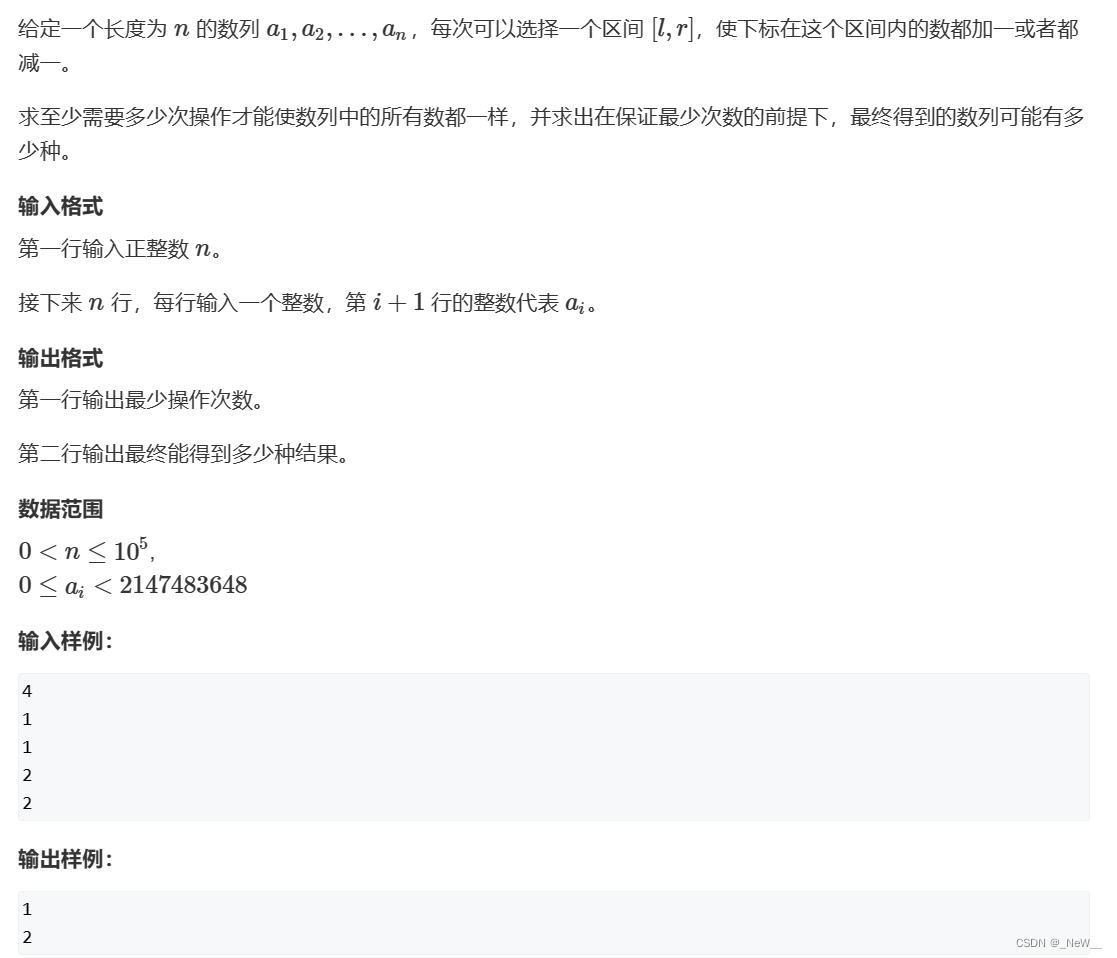
分析:要想把整个数组变为同一个数,我们可以根据差分的思想来做。
差分定义:b[1]=a[1]
b[2]=a[2]-a[1]
......
b[i]=a[i]-a[i-1]
由定义可知,可以把b[2]~b[n]全部变为0,那么整个数组就一样了。现在问题转换为如何用最少的操作次数把b[2]~b[n]全部变为0;由于差分数组操作是 b[ l ]+=1,b[ r+1 ]-=1/b[ l ]-=1,b[ r+1 ]+=1(操作的意思为在原数组a的区间[ l , r ] 加上1或减1)
那么对于2`~ n有四种操作(下边四种操作,l 和 r 都出现在了 1~ n中):
1. 2<=l , r <= n-1 (l,r都可以改变数组b 2~n 的值)b[l]+=1,b[r+1]-=1 /b[ l ]-=1,b[ r+1 ]+=1
2. l=1 ,2 <= r <= n-1 (只有r可以改变b数组 2~n的值) b[1]+=1,b[r+1]-=1 /b[ 1 ]-=1,b[ r+1 ]+=1
3. 2<= l <=n-1 ,r=n (只有 l 可以改变b数组 2~n的值,注意:虽然r=n,但是我们改变的是b[r+1] 的值) b[l]+=1,b[ r+1]-=1 /b[ l ]-=1,b[ r+1 ]+=1
4. l=1 , r=n 执行b[l]+=1,b[r+1]-=1 /b[ l ]-=1,b[ r+1 ]+=1,相当于在原数组上整体加1 或减1,无意义
我们的目的是把b数组的2~n的值变为0 ,且操作次数最少,那么我们优先使用操作1,执行完操作1后,b数组就只剩相同符号的数 了,然后再交替执行步骤 2和3(也可以只使用一个步骤,因为同一个步骤既可以加,也可以减,只是改变的值(b[1] 或 b[n+1])不一样) 就可以使b数组的2~n全部变为0
操作1为什么可以使b数组全部变为相同的数呢 ?因为可以任选两个数执行(加1和减1 ,也可以是减1和加1),最终留下的数,就是正数(正数之和大于负数)或者负数(负数的绝对值之和大于正数)(操作1的次数等于==== min(正数,abs(负数))
当全部变为正数或者负数时,那么就可以执行步骤2或3,即b数组的2~n中不为0的数,加或减,最后变为0 ,那么操作2和3的步骤次数为 (假如正数比负数大 , 那么就等于==正数-abs(负数),负数比正数大的话,同理;
求出在保证最少次数的前提下,最终得到的数列可能有多少种?
前面说了最终全部的数都会和b[1]相等,
那么最终的b[1]被操作几次,b[1]就可以有几种情况。即 上边操作2,3的次数 再+1,加1是因为b[1]原本还有一个数(可以只执行操作3),
最后一个知识点:假如有两个数 a>b 那么 max(a,b) = min(a,b) + (a-b)
代码
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
int a[N],b[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
b[i]=a[i]-a[i-1];
}
LL p=0,q=0;
for(int i=2;i<=n;i++)
{
if(b[i]>0) p+=b[i];
else q-=b[i];
}
cout<<max(p,q)<<endl<<abs(q-p)+1<<endl;
return 0;
}