目录
string的收尾
拷贝构造的现代写法:
浅拷贝:
拷贝构造的现代写法:
swap函数:
内置类型有拷贝构造和赋值重载吗?
完善拷贝构造的现代写法:
赋值重载的现代写法:
更精简的现代写法:
初学vector
插入数据:
访问vector的数据。
理解vector:
reserve:
resize
vector如何进行扩容:
算法题目
题目1:
题目2:
string的收尾
拷贝构造的现代写法:
浅拷贝:

其中,s1的_str指向字符串hello world,用s1拷贝构造s2:
s2(s1);当我们发生浅拷贝时,我们的s1的_str和s2的_str指向同一块空间:
如图所示:
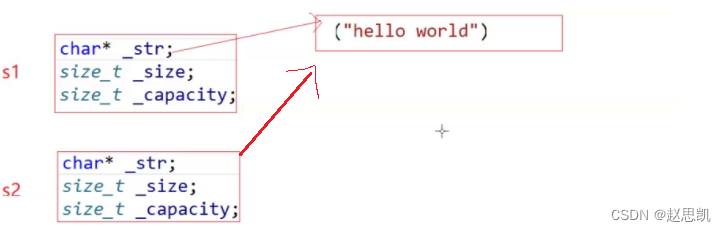
这就是所谓的浅拷贝。
浅拷贝的定义:
拷贝对象和源对象指向的空间是相同的。
浅拷贝造成的问题:
1:当s1调用完毕析构函数后,s2指向的空间也被析构了,s2也调用自己的析构函数,所以会导致一块空间被析构两次的问题。
2:对s1或s2其中一个对象的修改会导致另一个对象也发生变化。
拷贝构造的现代写法:
string(const string&s)
{
string tmp(s._str);
swap(_str, tmp._str);
swap(_size, tmp._size);
swap(_capacity, tmp._capacity);
}问题1:为什么这里的参数需要加上const
答:我们函数的目的是为了用s进行拷贝构造一个新的对象,所以我们最好不要对s本身进行修改,所以我们加上const表示s是只读的。
我们对代码进行理解:
string tmp(s._str);我们可以通过构造函数实现
我们首先调用构造函数
构造完毕如图所示:
swap(_str, tmp._str); swap(_size, tmp._size); swap(_capacity, tmp._capacity);接下来调用swap函数:
表示交换两个目标的值,我们把tmp的全部都与this指针指向的都西昂进行交换,如图所示:
那么我们的s2指向的内容就是"hello world"了,并且我们的s2和s1的_str并不相同,我们实现了深拷贝。
我们进行实验:
void test_string1()
{
string s1("hello world");
string s2(s1);
cout << s2.c_str() << endl;
} 
我们完成了拷贝构造的深拷贝。
问题1:如图:
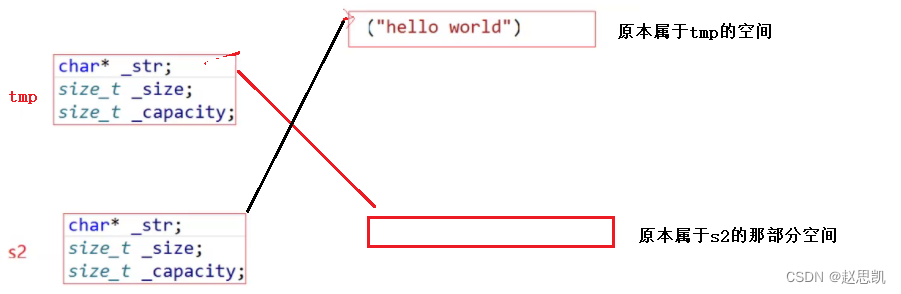
我们tmp现在指向的是原本属于s2的那部分空间,但是我们的s2并没有进行初始化,所以我们的s2指向的是随机值,我们的tmp是一个临时对象,函数栈帧调用完毕就会调用析构函数,我们delete函数对于野指针会报错。
我们如何预防这种问题呢?
答:我们可以使用初始化列表先把s2置为空指针,如代码所示:
string(const string&s)
:_str(nullptr)
,_size(0)
,_capacity(0)
{
string tmp(s._str);
swap(_str, tmp._str);
swap(_size, tmp._size);
swap(_capacity, tmp._capacity);
}delete对于空指针不做处理,所以不会报错。
swap函数:
s1.swap(s2);
swap(s1, s2);这两句代码有什么区别吗?
我们首先要清楚,这里调用了不同的swap函数,第一个调用的是string的接口swap函数:

第二个调用的是标准库里面的swap函数:

标准库的swap函数是用类摸板,通过调用三次拷贝构造来实现的。
那种更好更高效呢?
答:对于string的调用无疑是第一种更好更高效,因为我们的第二种调用了三次拷贝构造,调用三次string的拷贝构造,效率太低。
但是第一种是string的接口,我们的目的是模拟实现string,所以我们也要对string的swap函数进行模拟实现。
void swap(string&s)
{
swap(_str, s._str);
swap(_size, s._size);
swap(_capacity, s._capacity);
}这样写对吗?
不对,原因如下:
因为swap是在函数内部,首先在局部域找swap函数,找到了我们自己定义的swap函数,但是我们自己定义的swap函数只有一个参数,而我们调用swap函数却有两个参数,所以会报错,我们可以这样修改。
void swap(string&s)
{
std::swap(_str, s._str);
std::swap(_size, s._size);
std::swap(_capacity, s._capacity);
}我们使用域作用限定符,表示我们调用的swap是标准库里面的swap函数。

但是我们的标准库里面的swap函数需要调用三次拷贝构造,这个该怎么处理呢?
我们不需要考虑这个问题,因为我们swap调用的参数在这里全部是内置类型,对内置类型的拷贝构造不会造成效率的损失。
内置类型有拷贝构造和赋值重载吗?
答:原则上并没有,但是为了匹配摸板,不得不有,但是我们调用内置类型的拷贝构造和赋值重载和内置类型的初始化和赋值没有区别。
完善拷贝构造的现代写法:
string(const string&s)
:_str(nullptr)
,_size(0)
,_capacity(0)
{
string tmp(s._str);
swap(tmp);
}我们可以把原来的三个swap函数写成一个。
这个swap的本质是调用我们自己实现的string类里面的swap函数,其实等价于
this->swap(tmp);赋值重载的现代写法:
string s1("hello world");
string s3("hello bit");
s1 = s3;string&operator=(const string&s)
{
if (this != &s)
{
string tmp(s);
swap(tmp);
}
return *this;
}我们调用赋值重载函数需要返回*this,所以我们要用string&来接收。
我们进行判断,如果this和s的地址不相同,表示我们的s1和s3指向的不是同一块空间,我们调用赋值函数,首先调用拷贝构造,如图所示:
 我们直接把tmp和s1上的内容进行交换即可,原因是我们实现的拷贝构造是深拷贝,所以tmp和s3的内容相同,但是指向的空间是不同的,然后我们再把s1和tmp进行交换,交换之后的结果如图所示:
我们直接把tmp和s1上的内容进行交换即可,原因是我们实现的拷贝构造是深拷贝,所以tmp和s3的内容相同,但是指向的空间是不同的,然后我们再把s1和tmp进行交换,交换之后的结果如图所示:

更精简的现代写法:
string&operator=(string s)
{
swap(s);
return *this;
}我们的参数不传引用,既然不传引用,那么s就是s3的拷贝,s和s3指向的空间并不相同,然后我们调用swap函数即可。
初学vector

![]() vector是一个可以更改元素的数组,vector中可以存一种任意类型的数据。
vector是一个可以更改元素的数组,vector中可以存一种任意类型的数据。
插入数据:
#include<iostream>
#include<vector>
using namespace std;
void test_vector1()
{
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
cout << endl;
}
int main()
{
test_vector1();
return 0;
}我们进行调试:
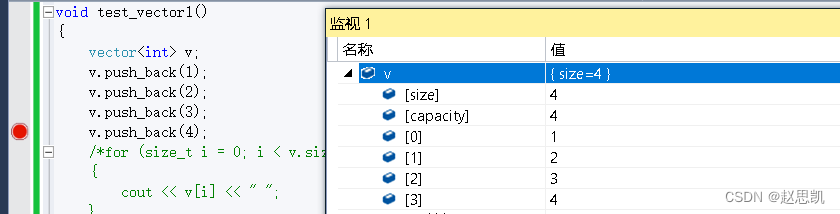
这就是所谓的插入函数。
访问vector的数据。
方法1:通过[]来进行访问:
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
for (size_t i = 0; i < v.size(); i++)
{
cout << v[i] << " ";
}
cout << endl;这种方法并不是万能的,string和vector中都有[],但是list中没有[]
方法2:通过迭代器访问:
vector<int>::iterator it = v.begin();
while (it != v.end())
{
cout << *it << " ";
++it;
}
cout << endl;这种方法是万能的,因为每一个接口都有迭代器。
方法3::通过范围for访问
for (auto ch : v)
{
cout << ch << " ";
}
cout << endl;范围for的底层其实是迭代器的另一种表达,所以没有迭代器也就没有范围for

理解vector:
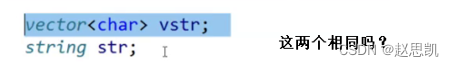
一个是内容是字符类型的vector,一个是string类。
他们是不同的,因为str的本质是字符串,而vstr的本质是数组,字符串的末尾一定是'\0',而数组没有这个要求。
string可以比较,以ascll码的形式进行比较,但是vector最好不要比较,原因是vector中不仅可能有内置类型,也有可能有自定义类型的内容。
reserve:

reserve函数的作用是修改容量。
我们思考一个问题:reserve函数可以缩容吗?
答:并不能,我们进行证明:
vector<int> v;
v.push_back(1);
v.push_back(2);
v.push_back(3);
v.push_back(4);
v.reserve(10);
cout << v.capacity() << endl;
v.reserve(4);
cout << v.capacity() << endl;
reserve函数并不能够缩容,原因是:因为缩容的代价太大,时间效率是最重要的,我们采用以空间换时间的思想,不对空间进行缩容。
resize

![]()
这里的size_type和value_type是什么意思?
size_type其实就是无符号整型的意思。
value_type就是vector中存放的数据类型。
![]()
这是什么意思?
这里的value_type我们可以等价为T().当我们这样写代码时:
v.resize(8);我们没有填写第二个参数,第二个参数的缺省值是value_type()。
这个value_type()本质是T(),假如我们的vector中的数据类型是string类型,那这个T()就是string类型的匿名对象,假如我们的vector中的数据类型是int类型,那这个T()就是int类的匿名对象也就是0,加入我们的vector中的数据类型是一个指针,那么这个T()就是指针的匿名对象也就是空指针。
我们可以这样吗?

不行,对于整形 浮点型,我们可以把其看作0,对于指针,我们可以把其看作空指针,但是对于自定义类型呢?自定义类型并不能用0初始化。
所以不能这样写。
vector如何进行扩容:
void TestVqectorExpand()
{
size_t sz;
vector<int> v;
sz = v.capacity();
cout << "making v grow:\n";
for (int i = 0; i < 100; i++)
{
v.push_back(i);
if (sz != v.capacity())
{
sz = v.capacity();
cout << "capacity changed:" << sz << '\n';
}
}
}这串代码可以检测我们的vector是如何进行扩容的。
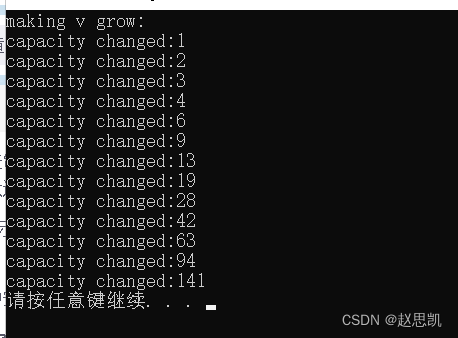
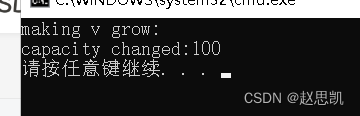
我们可以发现,扩容大概是每次扩容1.5倍,这样的好处是什么?
答:倍数过大时容易造成空间浪费,倍数过小容易导致频繁扩容。
扩容是有消耗的,为了防止扩容,我们可以使用reserve提前开好空间。

算法题目
题目1:
136. 只出现一次的数字 - 力扣(Leetcode)

我们需要了解^,异或表示相同为0,不同的话为1(针对的是二进位制)

这个数组中只出现一次的元素是4,我们如何找到4呢,我们可以进行异或:

我们知道相同的数字异或的结果为0,并且异或满足结合律

我们可以把相同的数字放在一起:

1异或1的结果为0,2异或2的结果为0,0异或0的结果为0,4异或0的结果为4.
异或:a^b,我们要进行判,加入a和b都为0时,结果为0,加入a或b其中一个为0,那结果就是另一个值,当a和b都不同且不为0,我们写出他们两个对应的二进位制,相同的二进位制的结果为0,不同的二进位制的结果为1,求出的二进位制对应的数字就是我们要的结果。
并且异或满足结合律,一组数组中,加入有相同的数字,这些数字我们可以把他们放在一起进行计算,计算的结果也是0。
所以我们可以这样写代码:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret=0;
for(auto ch:nums)
{
ret^=ch;
}
return ret;
}
};
题目2:
118. 杨辉三角 - 力扣(Leetcode)

假如我们用c语言写的话:

我们需要先malloc一个指针数组

我们需要再在指针数组上进行malloc申请空间。

我们在释放的时候,也需要先把一维数组释放掉,再释放二维数组。
可以发现,c语言写这道题目操作难度太大,我们可以用c++来写。
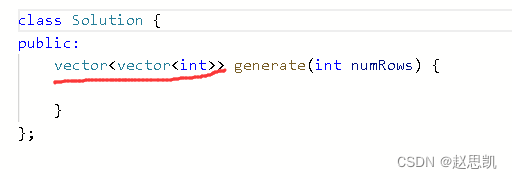
这里表示二维数组,generate首先是一个vector,vector中的元素的类型是vector<int>

class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> vv;
vv.resize(numRows);
for(size_t i=0;i<vv.size(),i++)
{
vv[i].resize(i+1);
vv[i][0]=vv[i][vv[i].size()-1]=1;
}
for(size_t i=0;i<vv.size();++i)
{
for(size_t j=0;j<vv[i].size();++j)
{
vv[i][j]=vv[i-1][j]+vv[i-1][j-1];
}
}
return vv;
}
};我们对代码进行逐步分析:
![]()
我们首先创建一个二维数组vector,接下来调用resize函数进行初始化,我们的vv的元素个数为numRows
![]()
我们调用resize函数,不传第二个参数,那第二个参数就是vector<int>类型的匿名对象,也就是0.
我们看杨辉三角有什么特点:

我们可以发现杨辉三角的每一行的首元素和尾元素都为1,并且每一行的元素个数都比前一行的元素个数多1个。

我们遍历数组的每一个元素,首先在每一个元素位置开辟对应的元素个数,然后把每一行的首元素和尾元素都置为空。
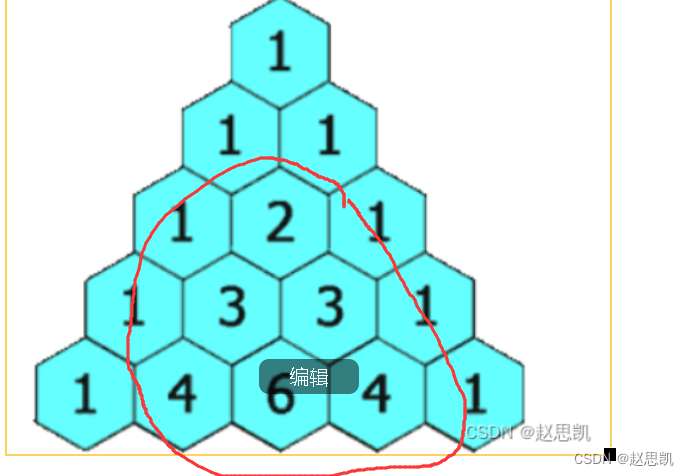
接下来,我们只需要实现这些中间元素即可。
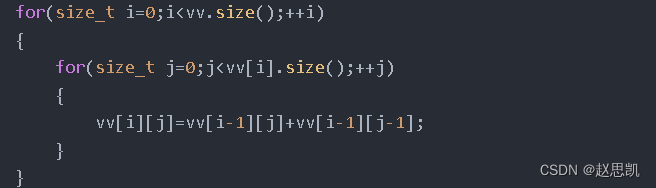
我们发现中间的每一个元素都为这个元素正上方的元素和正上方的左面一个单位的元素之和。
接下来,我们返回vv即可
![]()