1.相关概念
最小项:函数的某个乘积项包含了函数的全部变量(原变量或反变量的形式),且每个变量仅出现一次,则这个乘积项为该函数的一个标准积项。
最小项中的原变量记为1,反变量记为0,当变量顺序确定时即为一个二进制数。最小项通常用来表示,小标
即为其二进制数对应的十进制数。
例1:函数L(A,B,C)的最小项有:
![]()
分别对应有如下表示:
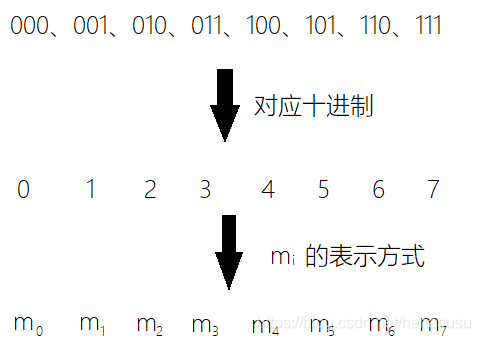
即:
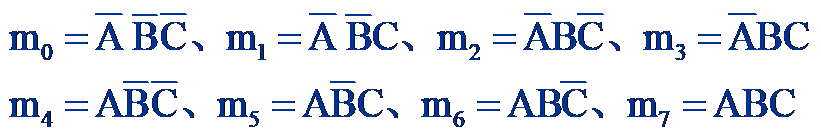
最小项的相邻性:如果两个最小项有且仅有一个因子或变量不同,则称这两个最小项为相邻最小项。
相邻最小项相加可以消去一个变量,合并为一项,如下:
![]()
2.卡诺图(karnaugh map)
2.1.基本知识点
①对于有n个变量的逻辑函数,其最小项有个,对应卡诺图也有
个小方格。
②卡诺图中的行列变量以格雷码(Gray Code)的形式变化,如此其几何相邻(上下或左右相邻,注意首尾行、首尾列也分别相邻)的小方格具有逻辑相邻性(两相邻小方格所对应的最小项有且仅有一个变量不同)。
例2:三变量的卡诺图如下

例3:逻辑函数![]() 的卡诺图如下
的卡诺图如下

2.2.逻辑函数的卡诺图化简法
2.2.1.逻辑函数按最小项形式补全
例4:逻辑函数![]() 利用
利用
![]()
![]()
![]()
补全为:
![]()
然后再转化为卡诺图(略)。
2.2.2.卡诺图化简(重点)
卡诺图相邻性的特点保证了几何相邻两方格所代表的最小项只有一个变量不同,故若相邻的方格都为1(简称1格)时,则对应的最小项就可以合并。合并的结果是消去这个不同的变量,只保留相同的变量,这是图形化简法的依据。
综上所述,卡诺图具备以下特性:
卡诺图中两个相邻1格的最小项可以合并成一个与项,并消去一个变量。
卡诺图中四个相邻1格的最小项可以合并成一个与项,并消去两个变量。
卡诺图中八个相邻1格的最小项可以合并成一个与项,并消去三个变量。
且卡诺图化简时遵循以下几点:
卡诺图中的1格都需要被画圈,可以重复但不能遗漏,否则最后得到的表达式就会与所给函数不等。
圈的个数应尽可能得少。因为一个圈和一个与项相对应,圈数越少则与或表达式的与项就越少。
按照2的整数次幂个方格来组合(即圈内的1格数必须为1,2,4,8...),圈的面积越大越好。因为圈越大可消去的变量就越多,与项中的变量就越少。
每个圈应至少包含一个新的1格,否则这个圈是多余的。
用卡诺图化简所得到的最简与或式不是唯一的。
例5:
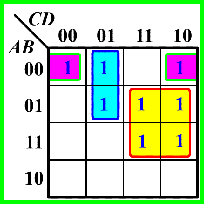


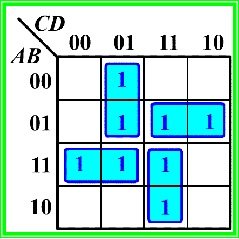
![]()
![]()
![]()
![]()
2.2.3.无关项
无关项包含两种情况:
①对于某一输入序列,其函数输出无关紧要。
②实际上不会发生或存在的输入。
对于无关项在卡诺图中用“x”表示,即可表示0也可表示1。
例6:

3.补充
3.1. 化简为或与式补充
也可利用卡诺图将函数化简为或与式,需要注意以下几点:
①最大项的概念:例如函数L(A,B,C)的最大项有,
等;
②0:原变量,1:反变量;
③卡诺图化简圈0,圈法同上;
④最后所有的和项相乘。
例7:









![[技术选型] ClickHouse和StarRocks的介绍](https://img-blog.csdnimg.cn/55ee2422d3364d3187b6fe70e3aa84a2.png)