数据结构 | 树 | 二叉树

news2024/11/30 6:51:55

 🔥Go for it!🔥
📝个人主页：按键难防
📫 如果文章知识点有错误的地方，请指正！和大家一起学习，一起进步👀

📖系列专栏：数据结构与算法
🔥 如果感觉博主的文章还不错的话，还请 点赞👍🏻收藏⭐️ + 留言📝​支持 一下博主哦

目录

树

二叉树：

二叉树定义方法（链式存储）：

层次建树实战：

 ①辅助队列（链式存储实现）：

②建树（源码）：

二叉树的遍历：

①前序遍历

②中序遍历

 ③后序遍历

④层次遍历

汇总：

树

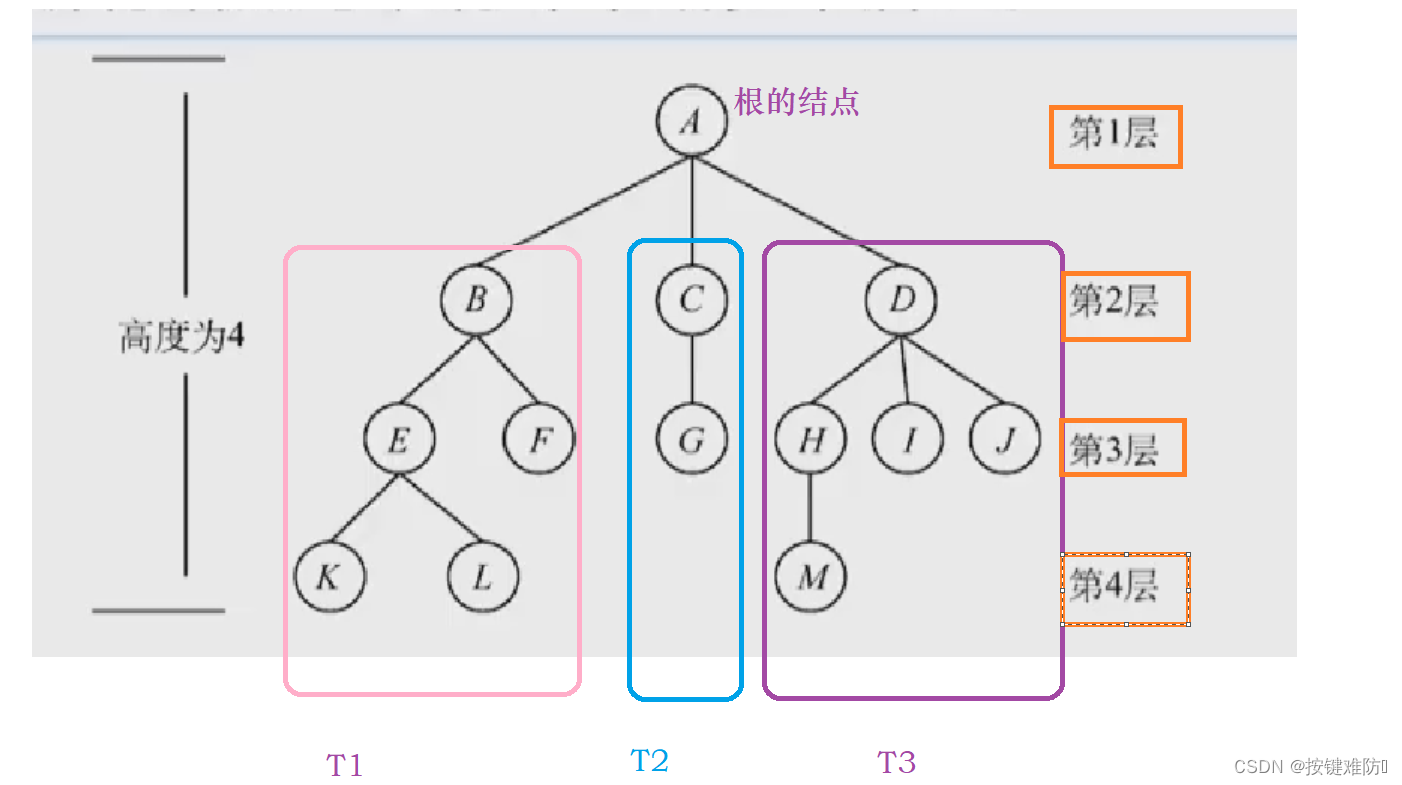
树是n（n ≥ 0）个节点的有限集。当n = 0时，称为空树。在任意一棵非空树中应满足：

1）有且仅有一个特定的结点的称为根的结点。

2）当n > 1时，其余节点可分为m（m > 0）个 互不相交的有限集T1, T2,…, Tm，其中每个集合 本身又是一棵树，并且称为根的子树。

特点：

树作为一种逻辑结构，同时也是一种分层结构，具 有以下两个特点：

1）树的根结点没有前驱，除根结点外的所有结点有且只有一个前驱。

2）树中所有结点可以有零个或多个后继。

二叉树：

二叉树是另一种树形结构，其特点是每个结点至多只有两棵子树 （即二叉树中不存在度大于2的结点），并且二叉树的子树有左右之分，其次序不能任意颠倒。 与树相似，二叉树也以递归的形式定义。二叉树是n（n ≥ 0）个 结点的有限集合：

① 或者为空二叉树，即n = 0。

② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。

满二叉树：
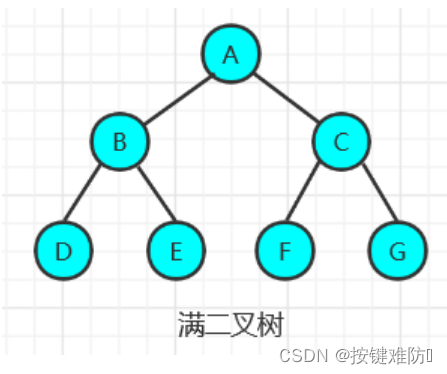
在一颗二叉树中，如果所有分支结点都有左子结点和右子结点，并且叶结点都集中在二叉树的最底层，这样的二叉树称为满二叉树。
 

完全二叉树：

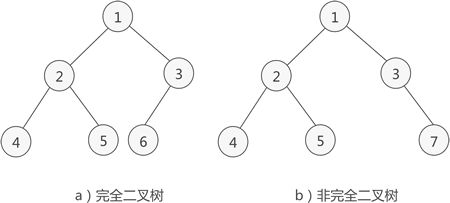
完全二叉树是由满二叉树引出的。满二叉树要求每一层的节点数都达到最大值，完全二叉树仅要求除最后一层外的节点数达到最大值，也就是说最后一层可以不满。但是最后一层从左往右不能有中断。

编程题 算法 中等 牛客网 NC60 判断一个树是否是搜索二叉树和完全二叉树

二叉树定义方法（链式存储）：

typedef char BiElemType;
typedef struct BiTNode{
	BiElemType c;//c就是书籍上的data
	struct BiTNode *lchild;//该二叉树的左孩子
	struct BiTNode *rchild;//该二叉树的右孩子
}BiTNode, *BiTree;
解释：typedef重命名了两个数据类型，
分别是将struct BiTNode重命名为BiTNode，将struct BiTNode*重命名为BiTree
前者是个结构体，后者是个指向该结构体的指针
用BiTNode创建变量，就是创建一个结构体（树的结点）
用BiTree创建变量，就是指向这个结构体的指针，用于接受动态内存开辟返回的指针

层次建树实战：

将"abcdefghij"用二叉树的方式存起来。

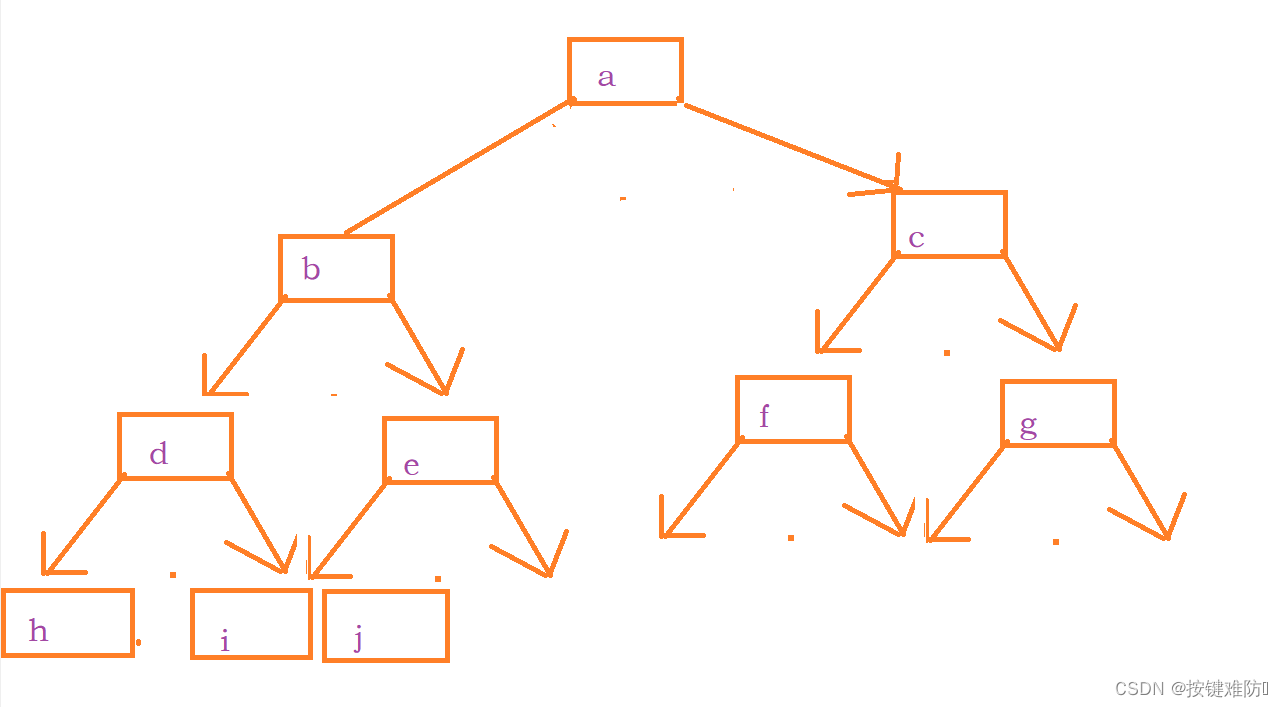
 ①辅助队列（链式存储实现）：

每多一个分支就当做一个元素入队，每当一个结点都有左右孩子，出队该节点。

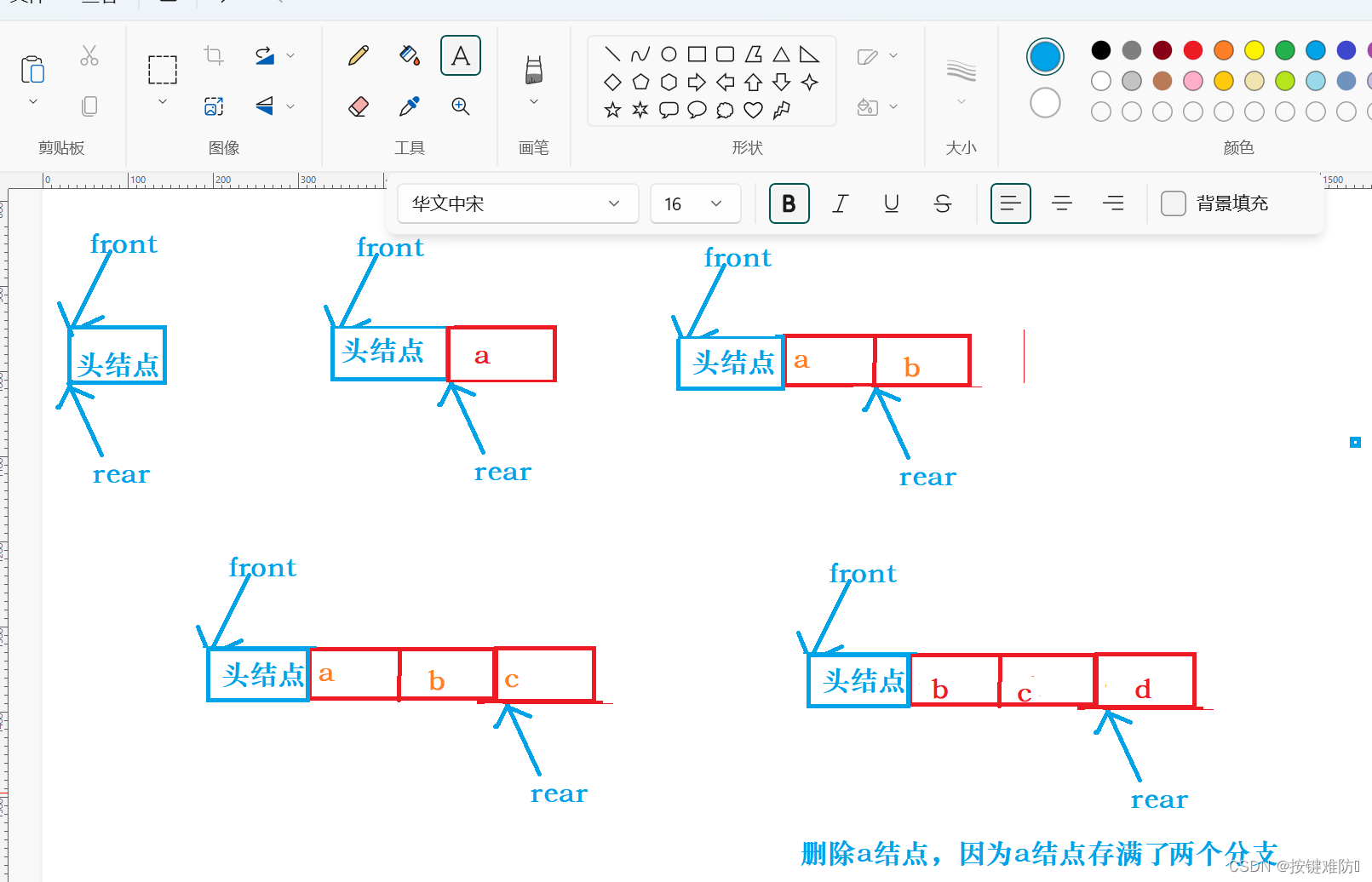
 所以只要满3个结点，就说明有一个树的结点存满两个分支，这样就需要删除第一个结点。

保证第一个结点始终不满两个分支。

实现：

typedef struct LinkNode//LinkNode结构体是辅助队列的结点
{
	BiTree p;//数据域，存放树的结点的地址值
	struct LinkNode *next;//指针域，辅助队列中下一个结点
}LinkNode;
typedef struct//结构体，用于存放辅助队列头结点和队列尾结点的指针
{	
	LinkNode* front, *rear;
}LinkQueue;
void InitQueue(LinkQueue &Q) //初始化头尾指针，就是创建头结点，然后头尾指针都指向这一头结点
{
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	//为辅助队列头结点申请空间
	//初始化时头尾指针都指向这一头结点
	Q.front->next = NULL;//头结点的next指针为NULL
}
void EnQueue(LinkQueue&Q, BiTree x)//入队，尾部插入法
{
	LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间
	s->p = x; s->next = NULL;//新申请的结点作为最后一个结点
	Q.rear->next =s;//先让前一结点（Q.rear）的指针域指向新插入的结点
	Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}
//出队 头部删除法
bool DeQueueF(LinkQueue &Q)
{
	//front始终指向头结点，但头结点什么都没存
	LinkNode *q = Q.front->next;//将第一个节点存入q
	Q.front->next = q->next;//断链，保留第一个结点的指针域，让头节点指向第二个结点
	free(q);
	return true;
}

②建树（源码）：

注释的很详细

#include <stdio.h>
#include <stdlib.h>
typedef char BiElemType;
typedef struct BiTNode{
	BiElemType data;
	struct BiTNode *lchild;
	struct BiTNode *rchild;
}BiTNode, *BiTree;
typedef struct LinkNode//LinkNode结构体是辅助队列的结点
{
	BiTree p;//树的某一个结点的地址值，不是数值
	struct LinkNode *next;//辅助队列中下一个结点
}LinkNode;
typedef struct //结构体，用于存放辅助队列头结点和队列尾结点的指针
{	
	LinkNode* front, *rear;
}LinkQueue;
void InitQueue(LinkQueue &Q) //初始化头尾指针，就是创建头结点，然后头尾指针都指向这一头结点
{
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	//为辅助队列头结点申请空间
	//初始化时头尾指针都指向这一头结点
	Q.front->next = NULL;//头结点的next指针为NULL
}
void EnQueue(LinkQueue&Q, BiTree x)//入队，尾部插入法
{
	LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间
	s->p = x; s->next = NULL;//新申请的结点作为最后一个结点
	Q.rear->next =s;//先让前一结点（Q.rear）的指针域指向新插入的结点
	Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}
//出队 头部删除法
bool DeQueueF(LinkQueue &Q)
{
	//front始终指向头结点，但头结点什么都没存
	LinkNode *q = Q.front->next;//将第一个节点存入q
	Q.front->next = q->next;//断链，保留第一个结点的指针域，让头节点指向第二个结点
	free(q);
	return true;
}
int main()//二叉树的建树（层次建树）
{
	LinkQueue Q;//创建辅助队列头尾指针
	InitQueue(Q);//初始化头尾指针
	BiTree pnew;//用来指向新申请的树结点的指针
	BiTree tree = NULL;//树根的指针
	char c;
	//输入内容为 abcdefghij
	while (scanf("%c", &c))
	{
		if (c == '\n')
		{
			break;
		}
		pnew = (BiTree)calloc(1, sizeof(BiTNode));//calloc申请空间并对空间进行初始化，赋值为0
		pnew->data = c;//数据放进去
		EnQueue(Q, pnew);//将新创建的树的结点的地址入队辅助队列
		//下面是建树的过程
		if (NULL == tree)//空树
		{
			tree = pnew;  //tree指向树的根节点
			continue;//该节点为树的第一个节点
			//直接跳到循环的判断部分
		}
		else 
		 {
			if (NULL == Q.front->next->p->lchild)//如何把新结点放入树
			{//Q.front->next为辅助队列第一个结点
				Q.front->next->p->lchild = pnew;//把新结点放到要插入结点的左边
			}
			else if (NULL == Q.front->next->p->lchild)
			{
				Q.front->next->p->rchild = pnew;//把新结点放到要插入结点的右边
				DeQueue(Q);//左右都放了结点后，辅助队列该删除第一个节点了
				//该函数只用于出队，不保存出队结点的数据}
		}
	}
	return 0;
}

二叉树的遍历：

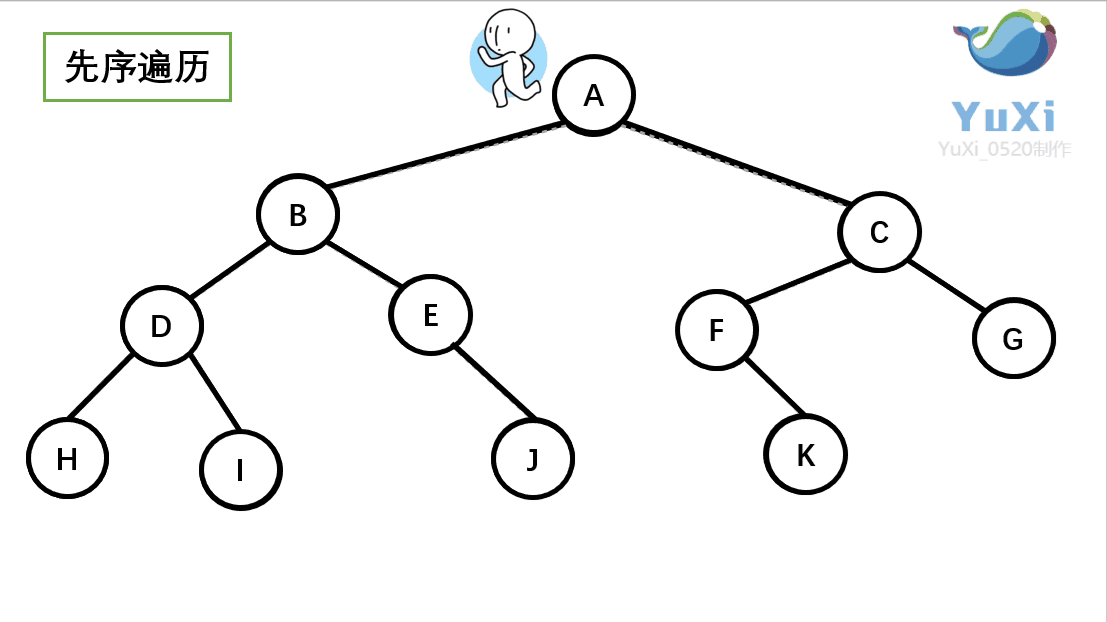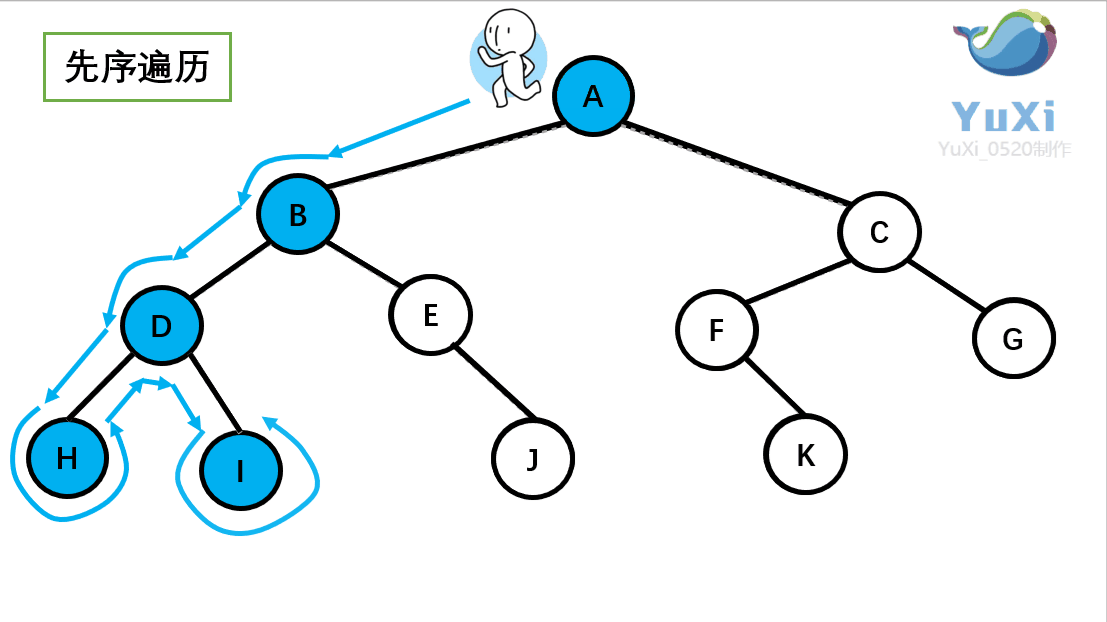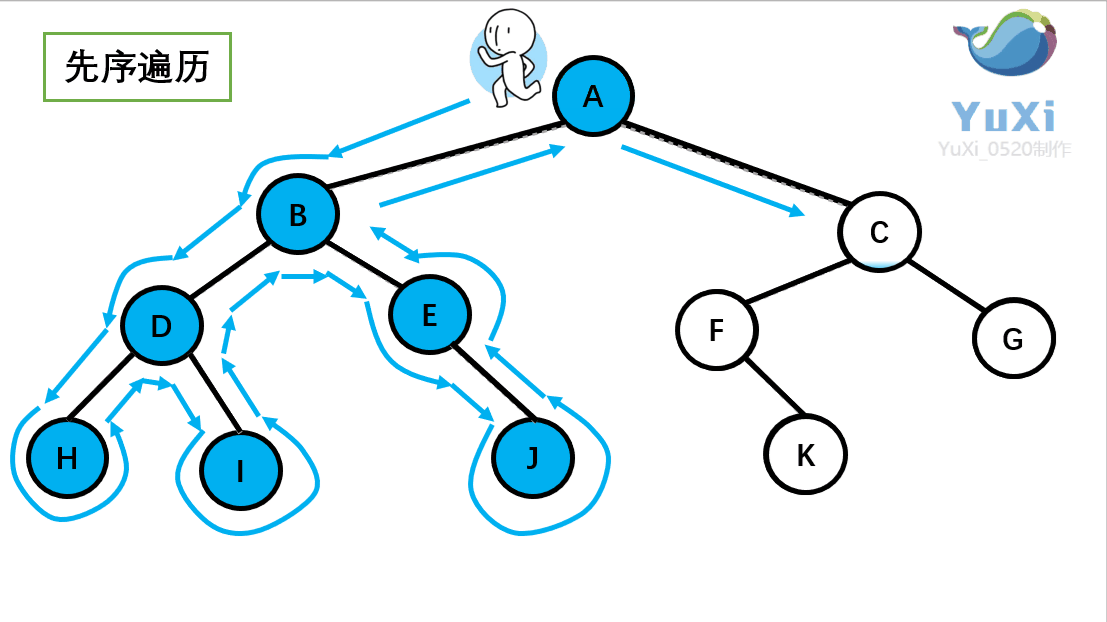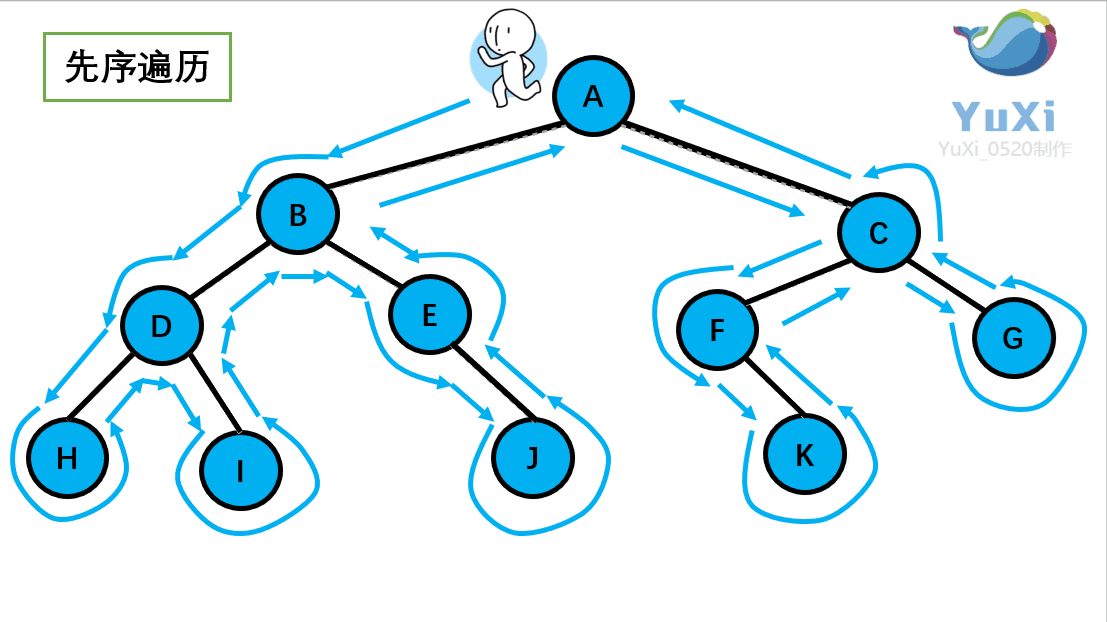
①前序遍历

首先前序遍历是先打印自身，再打印左子树，再打印右子树，我们通 过 PreOrder 函数来实现

//递归实现
//abdhiejcfg 前序遍历，前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{
	if (p != NULL)
	{
		putchar(p->data);
		PreOrder(p->lchild);
		PreOrder(p->rchild);
	}
}

②中序遍历

中序遍历是先打印左子树，再打印当前结点，再打印右子树，我 们通过 InOrder 函数来实现。

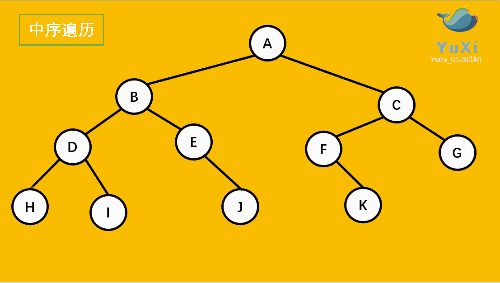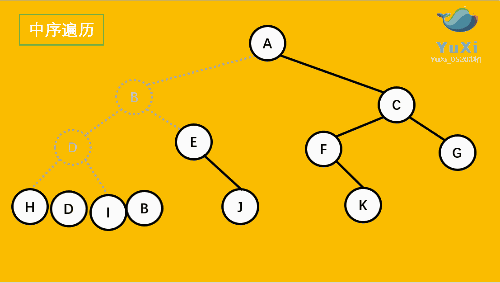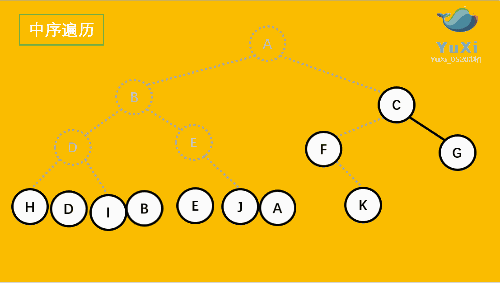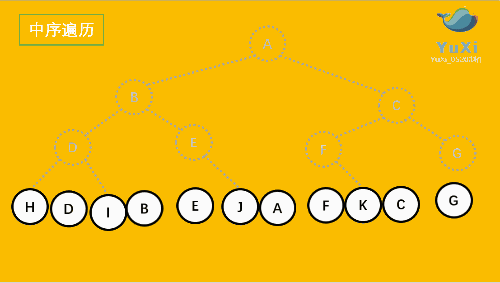
//中序遍历 hdibjeafcg
void InOrder(BiTree p)
{
	if (p != NULL)
	{
		InOrder(p->lchild);
		putchar(p->data);
		InOrder(p->rchild);
	}
}

 ③后序遍历

后序遍历是先打印左子树，再打印右子树，最后打印当前结点， 我们通过 PostOrder 函数来实现。

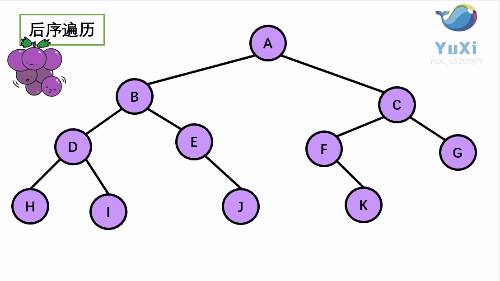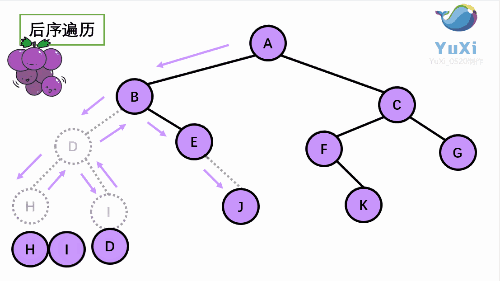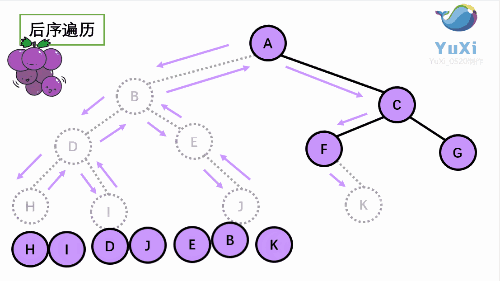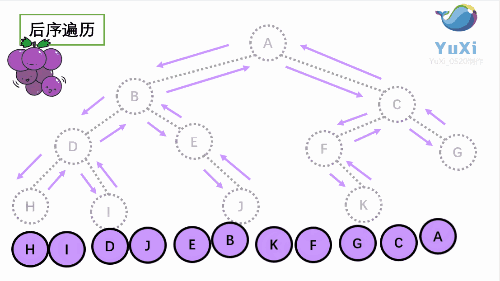
//hidjebfgca 后序遍历
void PostOrder(BiTree p)
{
	if (p != NULL)
	{
		PostOrder(p->lchild);
		PostOrder(p->rchild);
		putchar(p->data);
	}
}

④层次遍历

二叉树的层次遍历 ，顾名思义就是指从二叉树的第一层（根节点）开始，从上至下逐层遍历，在同一层中，则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中，按从顶层到底层的次序访问树中元素，在同一层中，从左到右进行访问。

树根的地址作为辅助队列的第一个结点的数据域，然后删除第一个结点，保留数据域，然后借助树根的地址让自己的左孩子(b)和右孩子(c)分别入队，然后打印左孩子数据域(b)，再入队左孩子的两个分支(de)，然后打印右孩子的数据域，入队右孩子的两个分支(fg)，然后一直这样循环。就可以把树连根拔起。

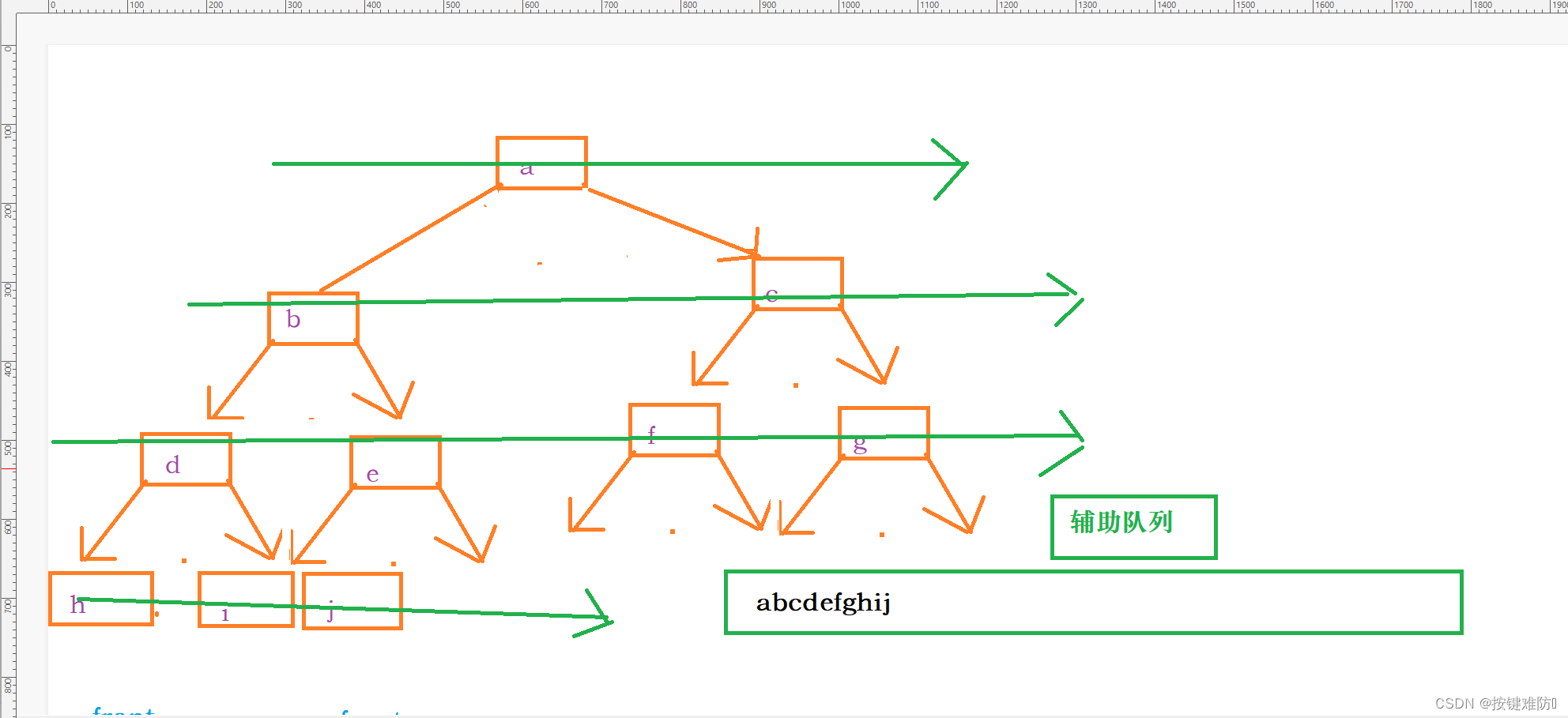
void LevelOrder(BiTree T)
{
	LinkQueue Q1;//辅助队列
	InitQueue(Q1);//初始化队列
	BiTree p;//存储出队的结点
	EnQueue(Q1, T);//树根入队
	while (!IsEmpty(Q1))//！是逻辑反操作
	{//队列不是空，循环继续
		DeQueue(Q1,p);//出队当前结点
        //p是出队结点的数据域，借助它找到出队结点指向的树的结点的左右孩子
		putchar(p->data);//打印数据域
		if (p->lchild != NULL) //入队左孩子
		{
			EnQueue(Q1, p->lchild);
		}
		if (p->rchild != NULL) //入队右孩子
		{
			EnQueue(Q1, p->rchild);
		}
	}

汇总：

#include <stdio.h>
#include <stdlib.h>
typedef char BiElemType;
typedef struct BiTNode{
	BiElemType data;
	struct BiTNode *lchild;
	struct BiTNode *rchild;
}BiTNode, *BiTree;
typedef struct LinkNode//LinkNode结构体是辅助队列的结点
{
	BiTree p;//树的某一个结点的地址值，不是数值
	struct LinkNode *next;//辅助队列中下一个结点
}LinkNode;
typedef struct //结构体，用于存放辅助队列头结点和队列尾结点的指针
{	
	LinkNode* front, *rear;
}LinkQueue;
void InitQueue(LinkQueue &Q) //初始化头尾指针，就是创建头结点，然后头尾指针都指向这一头结点
{
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	//为辅助队列头结点申请空间
	//初始化时头尾指针都指向这一头结点
	Q.front->next = NULL;//头结点的next指针为NULL
}
bool IsEmpty(LinkQueue Q)
{
	if (Q.front == Q.rear)
		return true;
	else
		return false;
}
void EnQueue(LinkQueue&Q, BiTree x)//入队，尾部插入法
{
	LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间
	s->p = x; s->next = NULL;//新申请的结点作为最后一个结点
	Q.rear->next =s;//先让前一结点（Q.rear）的指针域指向新插入的结点
	Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}
//出队 头部删除法
bool DeQueueF(LinkQueue &Q)
{//不保存删除结点数据域
	//front始终指向头结点，但头结点什么都没存
	LinkNode *q = Q.front->next;//将第一个节点存入q
	Q.front->next = q->next;//断链，保留第一个结点的指针域，让头节点指向第二个结点
	free(q);
	return true;
}
bool DeQueue(LinkQueue &Q, BiTree &x)//出队
{//x用于保存删除结点的数据域
	if (Q.front == Q.rear)
	{
		return false;
	}//队列为空
	//front始终指向头结点，但头结点什么都没存
	LinkNode *q = Q.front->next;//将第一个节点存入q
	x = q->p;//获取要出队结点存储的值
	Q.front->next = q->next;//断链，保留第一个结点的指针域，让头节点指向第二个结点
	if (Q.rear == q)//删除的是最后一个元素
	{
		Q.rear = Q.front;//队列置为空
	}
	free(q);
	return true;
}
// 递归实现
//abdhiejcfg 前序遍历，前序遍历就是深度优先遍历
void PreOrder(BiTree p)
{
	if (p != NULL)
	{
		putchar(p->data);
		PreOrder(p->lchild);
		PreOrder(p->rchild);
	}
}
//中序遍历 hdibjeafcg
void InOrder(BiTree p)
{
	if (p != NULL)
	{
		InOrder(p->lchild);
		putchar(p->data);
		InOrder(p->rchild);
	}
}
//hidjebfgca 后序遍历
void PostOrder(BiTree p)
{
	if (p != NULL)
	{
		PostOrder(p->lchild);
		PostOrder(p->rchild);
		putchar(p->data);
	}
}
void LevelOrder(BiTree T)
{
	LinkQueue Q1;//辅助队列
	InitQueue(Q1);//初始化队列
	BiTree p;//存储出队的结点
	EnQueue(Q1, T);//树根入队
	while (!IsEmpty(Q1))//！是逻辑反操作
	{//队列不是空，循环继续
		DeQueue(Q1,p);//出队当前结点
        //p是出队结点的数据域，借助它找到出队结点指向的树的结点的左右孩子
		putchar(p->data);//打印数据域
		if (p->lchild != NULL) //入队左孩子
		{
			EnQueue(Q1, p->lchild);
		}
		if (p->rchild != NULL) //入队右孩子
		{
			EnQueue(Q1, p->rchild);
		}
	}
int main()//二叉树的建树（层次建树）
{
	LinkQueue Q;//创建辅助队列头尾指针
	InitQueue(Q);//初始化头尾指针
	BiTree pnew;//用来指向新申请的树结点的指针
	BiTree tree = NULL;//树根的指针
	BiTree de;//
	char c;
	//输入内容为 abcdefghij
	while (scanf("%c", &c))
	{
		if (c == '\n')
		{
			break;
		}
		pnew = (BiTree)calloc(1, sizeof(BiTNode));//calloc申请空间并对空间进行初始化，赋值为0
		pnew->data = c;//数据放进去
		EnQueue(Q, pnew);//将新创建的树的结点的地址入队辅助队列
		//下面是建树的过程
		if (NULL == tree)//空树
		{
			tree = pnew;  //tree指向树的根节点
			continue;//该节点为树的第一个节点
			//直接跳到循环的判断部分
		}
		else 
		 {
			if (NULL == Q.front->next->p->lchild)//如何把新结点放入树
			{//Q.front->next为辅助队列第一个结点
				Q.front->next->p->lchild = pnew;//把新结点放到要插入结点的左边
			}
			else if (NULL == Q.front->next->p->rchild)
			{
				Q.front->next->p->rchild = pnew;//把新结点放到要插入结点的右边
				DeQueueF(Q);//左右都放了结点后，辅助队列该删除第一个节点了
				//该函数只用于出队，不保存出队结点的数据
			}
		}
	}
	printf("--------前序遍历----------\n");//也叫先序遍历，先打印当前结点，打印左孩子，打印右孩子
		PreOrder(tree);
	printf("\n--------中序遍历------------\n");//先打印左孩子，打印父亲，打印右孩子
	InOrder(tree);
	printf("\n--------后序遍历------------\n");//先打印左孩子，打印右孩子，最后打印父亲
	PostOrder(tree);
	printf("\n--------层次遍历-----------\n");
	LevelOrder(tree);
	printf("\n");
	return 0;
}

效果： 

希望这篇文章📃能对你有所帮助😁😁 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/344503.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

windows本地开发Spark[不开虚拟机]

windows本地开发Spark[不开虚拟机]

1. windows本地安装hadoop hadoop 官网下载 hadoop2.9.1版本 1.1 解压缩至C:\XX\XX\hadoop-2.9.1 1.2 下载动态链接库和工具库 1.3 将文件winutils.exe放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.4 将文件hadoop.dll放在目录C:\XX\XX\hadoop-2.9.1\bin下 1.5 将文件hadoop.dl…
阅读更多...
Redis学习【5】之集合的底层实现原理

Redis学习【5】之集合的底层实现原理

文章目录一 集合的底层实现原理1.1 两种实现的选择1.2 zipList【存在于Redis7.0之前的版本】1.3 listPack【Redis7.0中zipList的改进版】1.4 skipList1.4.1 skipList 原理1.4.2 skipList存在的问题与优化1.5 quickList1.5.1 quitList检索操作1.5.2 quitList插入操作1.5.3 quitL…
阅读更多...
知识图谱概述

知识图谱概述

知识图谱 知识图谱本质上是一种大规模的语义网络&#xff0c;富含实体、概念及其之间的各种语义关系。 作为一种语义网络是大数据时代知识表示的重要方式之一。 作为一种技术体系&#xff0c;是大数据时代知识工程代表性进展。 领域知识图谱 领 域&#xff08;行业&#xf…
阅读更多...
一篇文章带你熟练使用Ansible中的playbook

一篇文章带你熟练使用Ansible中的playbook

目录 一、Playbook的功能 二、YAML 1、简介 2、特点 3、语法简介 4、YAML 列表 5、YAML的字典 三、playbook执行命令 四、 Playbook的核心组件 五、vim 设定技巧 练习 一、Playbook的功能 playbook 是由一个或多个play组成的列表 Playboot 文件使用YAML来写的 二、…
阅读更多...
Mysql5.7安装【Windows版】

Mysql5.7安装【Windows版】

文章目录一、下载二、添加到环境变量三、添加配置文件my.ini四、安装Mysql 修改密码一、下载 下载地址 滑倒最下面有一个MySQL Community Server 选择要下载的版本 二、添加到环境变量 下载好了之后开始解压 把bin目录添加到环境变量 可以点击进入bin目录&#xff0c;直接复…
阅读更多...
低代码平台真的是企业的福音吗？

低代码平台真的是企业的福音吗？

研究低代码平台已有3年&#xff0c;也算是个低代码资深用户了&#xff0c;下面基于个人理解给大家做一份2k字的深入介绍&#xff01;希望对大家在低代码方面有一定帮助。 开篇&#xff0c;先带大家来看企业为什么要布局低代码平台&#xff01;究竟有何优势&#xff1f; &…
阅读更多...
认识钉钉小程序_搭建一个简单的小程序---钉钉小程序开发教程001

认识钉钉小程序_搭建一个简单的小程序---钉钉小程序开发教程001

其实这里面开发的时候具体,应该有很多的坑,不过..因为暂时不需要具体做,我仅仅查了一下怎么做,记录一下,以后不用再查了. 感觉钉钉小程序开发比微信小程序开发要更便捷,简单一些.首先要注册一个开发者,其实登录上钉钉账号就可以了.然后可以看看,快速入门,我没看 然后下载开发工…
阅读更多...
Java基础之多线程JUC全面学习笔记

Java基础之多线程JUC全面学习笔记

目录初识多线程多线程的实现方式常见的成员方法线程安全的问题死锁生产者和消费者线程池自定义线程池初识多线程 什么是多线程? 线程 线程是操作系统能够进行运算调度的最小单位。线程被包含在进程之中&#xff0c;是进程中的实际运作单位。 简单理解:应用软件中互相独立&…
阅读更多...
为什么西门子、美的等企业这样进行架构升级，看看改造效果就知道了

为什么西门子、美的等企业这样进行架构升级，看看改造效果就知道了

在工业领域&#xff0c; 生产、测试、运行阶段都可能会产生大量带有时间戳的传感器数据&#xff0c;这都属于典型的时序数据。时序数据主要由各类型实时监测、检查与分析设备所采集或产生&#xff0c;涉及制造、电力、化工、工程作业等多个行业&#xff0c;具备写多读少、量非常…
阅读更多...
从端到端打通模型端侧部署流程（NCNN）

从端到端打通模型端侧部署流程（NCNN）

文章目录背景介绍&#xff1a;为什么要做端侧推理&#xff1a;端侧深度学习部署流程&#xff1a;一条主要技术路线&#xff1a;ONNX&#xff1a;NCNN框架&#xff1a;NCNN的官方介绍&#xff1a;NCNN问题解决&#xff1a;NCNN使用样例快速在NCNN框架下验证自己的模型&#xff1…
阅读更多...
数据分析思维（六）｜循环/闭环思维

数据分析思维（六）｜循环/闭环思维

循环/闭环思维 1、概念 在很多的分析场景下&#xff0c;我们需要按照一套流程反复分析&#xff0c;而不是进行一次性的分析&#xff0c;也就是说这套流程的结果会成为该流程的新一次输入&#xff0c;从而形成一个闭环&#xff0c;此时的分析思维我们称之为循环/闭环思维。 常…
阅读更多...
计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性

计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性

计算机断层扫描结肠镜和全自动骨密度仪在一次检查中的可行性 Feasibility of Simultaneous Computed Tomographic Colonography and Fully Automated Bone Mineral Densitometry in a Single Examination 简单总结&#xff1a; 数据&#xff1a;患者的结肠镜检查和腹部CT检查…
阅读更多...
2022黑马Redis跟学笔记.实战篇(三)

2022黑马Redis跟学笔记.实战篇(三)

2022黑马Redis跟学笔记.实战篇 三4.2.商家查询的缓存功能4.3.1.认识缓存4.3.1.1.什么是缓存4.3.1.2.缓存的作用1.为什么要使用缓存2.如何使用缓存3. 添加商户缓存4. 缓存模型和思路4.3.1.3.缓存的成本4.3.2.添加redis缓存4.3.3.缓存更新策略4.3.3.1.三种策略(1).内存淘汰:Redis…
阅读更多...
NoSQL和Redis

NoSQL和Redis

NoSQL一、NoSqlNoSQL Not Only SQL(不仅仅是SQL)非关系型数据库二、为什么需要NoSQL1、web1.0在90年代&#xff0c;一个网站的访问量一般都不大&#xff0c;用单个数据库完全可以轻松应付。在那个时候&#xff0c;更多的都是静态网页&#xff0c;动态交互类型的网站不多。单机…
阅读更多...
CS224W课程学习笔记（一）：课程介绍与图深度学习概念

CS224W课程学习笔记（一）：课程介绍与图深度学习概念

引言 我们从怎么利用图形或网络表示数据这一动机开始。网络成为了用于描述复杂系统中交互实体的通用语言。从图片上讲&#xff0c;与其认为我们的数据集由一组孤立的数据点组成&#xff0c;不如考虑这些点之间的相互作用和关系。 在不同种类的网络之间进行哲学上的区分是有启…
阅读更多...
系统功能设计：教育缴费平台产品需求文档

系统功能设计：教育缴费平台产品需求文档

教育缴费系统后台能够支撑前端业务&#xff0c;查询所需字段&#xff0c;为支撑前端业务提供服务&#xff0c;支持学校分校管理、班级分班管理、账单撤回及强制结束等功能。为了将教育缴费的需求清晰准确地描述清楚&#xff0c;本文作者编写了这个产品需求文档&#xff0c;一起…
阅读更多...
Jmeter自带函数不够用？不如自己动手开发一个

Jmeter自带函数不够用？不如自己动手开发一个

在Jmeter的函数助手里&#xff0c;有很多内置的函数&#xff0c;比如Random、UUID、time等等。使用这些函数可以快速帮我们生成某些数据&#xff0c;进行一些逻辑处理。用起来非常的方便。 但是在实际接口测试过程中&#xff0c;有很多的需求&#xff0c;Jmeter内置的函数可能…
阅读更多...
对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析

对抗生成网络GAN系列——Spectral Normalization原理详解及源码解析

&#x1f34a;作者简介&#xff1a;秃头小苏&#xff0c;致力于用最通俗的语言描述问题 &#x1f34a;专栏推荐&#xff1a;深度学习网络原理与实战 &#x1f34a;近期目标&#xff1a;写好专栏的每一篇文章 &#x1f34a;支持小苏&#xff1a;点赞&#x1f44d;&#x1f3fc;、…
阅读更多...
JavaEE-HTTP协议(二)

JavaEE-HTTP协议(二)

目录HTTP请求的方法GET方法POST 方法其他方法“报头”User-AgentRefererCookieHTTP响应200 OK404 Not Found403 Forbidden405 Method Not Allowed500 Internal Server Error504 Gateway Timeout302 Move temporarily301 Moved PermanentlyHTTP请求的方法 GET方法 GET 是最常用…
阅读更多...
Jmeter之直连数据库框架搭建简介

Jmeter之直连数据库框架搭建简介

案例简介 通过直连数据库让程序代替接口访问数据库&#xff0c;如果二者预期结果不一致&#xff0c;就找到了程序的缺陷。 下面通过一个案例分析讲解如何实现&#xff1a;获取某个字段值&#xff0c;放在百度上搜索。 实现方式 1、Jmeter本身不具备直连数据库的功能&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023