文章目录
- 开始
- 基本思路:“反悔”机制
- 干活
- 尝试一:深度优先搜索
- 尝试二:少走弯路
- 尝试三:最短增广路径,广度优先
- 还是没ac
- 记两个小bug
- 1. 数组越界
- 2. 写错变量名
- 小结
- 最后一个版本的代码(C++)
- 定义类与函数
- 主函数
- 类与函数的调试版本
开始
已多次看到“网络最大流问题”的字眼,一直不知道是什么,后来终于有一次打算仔细了解一下,期间我发现了一篇不错的博客:全面理解网络流中的最大流问题。在这篇博客的帮助下,我成功弄清楚了什么是网络流中的最大流问题,同时也明白了解决这个问题的基本思路。
基本思路:“反悔”机制
(这里不仔细介绍思路了,大家可以先看看前面那篇博客)
在前面提到的博客中,博主认为“借用”这个描述比“反悔”更为合适。然而在阅读的过程中,我反而理解了“反悔”这个概念,同时觉得还挺合适的。下面简单说说自己关于“反悔”的理解。
首先说说为什么会需要“反悔”。举个有点抽象的例子,在某个网络中,A只有一条路可走,B却率先占用了A唯一的路径,然而其实B还有其它空闲的路径可走,以至于网络的运载能力没有被充分利用,不是“最大流”。于是A告诉B:你挡着道了,B听到后就换了一条路走,A便也得以通过。
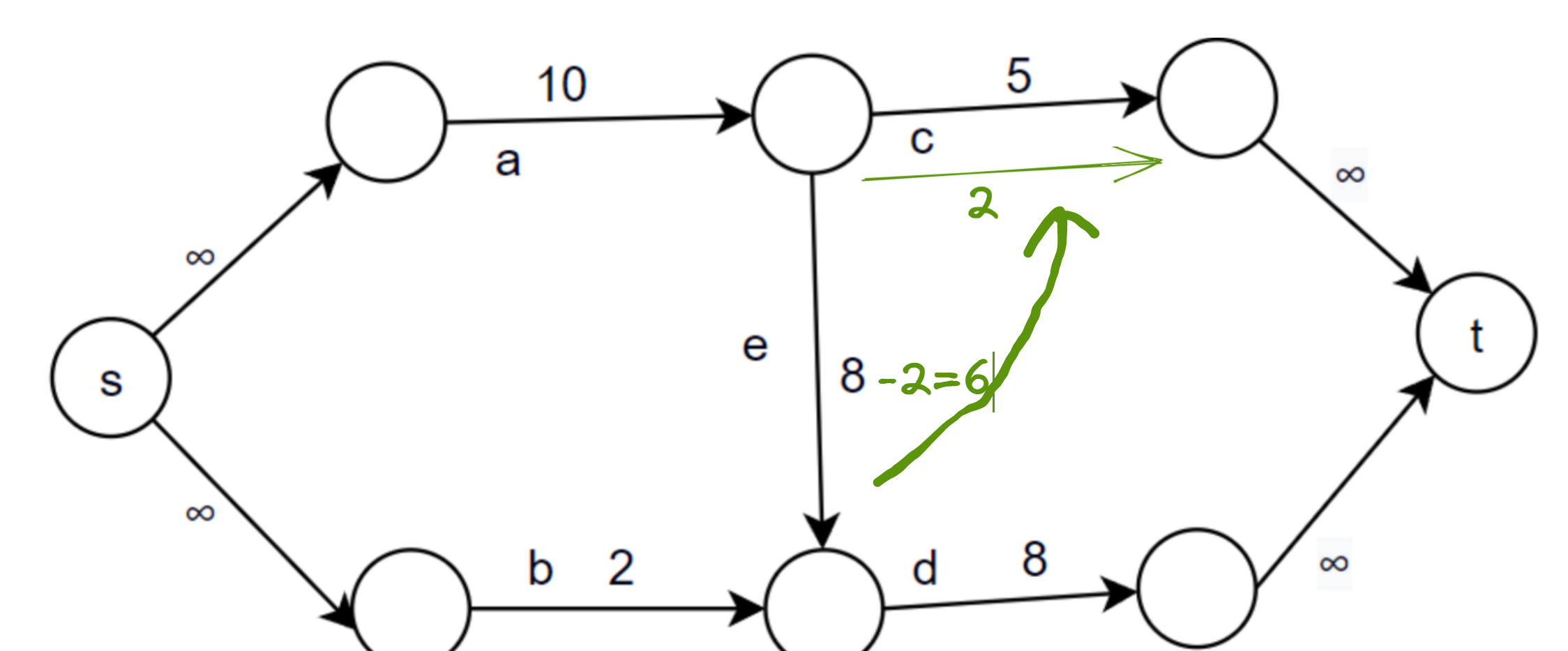
我们看看下面这个网络(来自前面提到的博客):
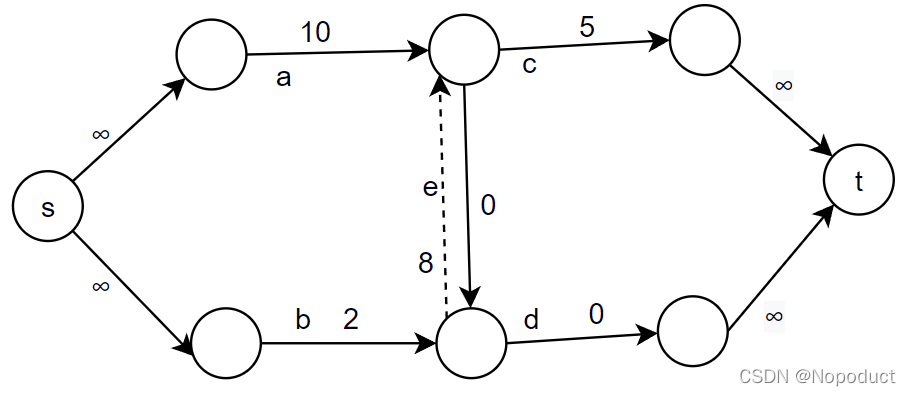
如果选择路径的顺序为:
1、a -> e -> d = 8(有流量8通过这条路径)
2、a -> c = 2
那么从路径b过来的流量就被阻塞了。
而如果我们在通过路径e时,建立一条与通过流量相同的反向边 e’ ,表示走这条路径的选择是可以反悔的,最大可反悔流量为8。那么当流量A通过路径b后,发现了可反悔的路径e,就告诉以占用e的流量B:你挡着道了。于是B的两个流量就从 e’ 返回,然后通过c边到达了终点t。而路径d也腾出了2个流量,A就从原先流量B占用的路径通过。于是有:
3、b -> e’ -> c = 2
得到最大流 8 + 2 + 2 = 12
干活
我对于自己测试代码的能力不太自信,于是从洛谷上找了个题:P3376 【模板】网络最大流
尝试一:深度优先搜索
算法过程采用深度优先搜索,从 源点 开始,到每个点时记录流入该点的流量,然后将这些流量分向其它的点,通过边时就更新边的剩余流量,到达 汇点 时就累加更新最大流。对于有分叉出路的点,通过边的同时建立反向边。
于是我遇到了一些问题:
- 不应当在搜索过程中刚经过一条边(一个点)时就更新它的剩余流量,因为实际通过流量会受后面的影响。(从源点到汇点一条路径的流量,由路径上流量最小的边决定)
- 解决方案:在遍历时记录走过的点,在达到汇点时再更新整条路径所有边(点)的剩余流量
结果在部分测试集上超时了。
尝试二:少走弯路
我起初并没有去查找其它的算法,而想自己在原来算法过程的基础上优化试试。于是我作出了一个假设:很多时间浪费在已经不可能的方向上。
于是我尝试引入一种点死亡机制,在搜索过程中,如果从一个点某次没能成功到达汇点,就判定这个点已经寄了,以后再也不走这里了。
但我后面发现了问题:
- 在搜索过程中判定点的死亡并不合适。因为在搜索时,我并不会再走已经走过的点,而一个被判定为寄了的点,可能经过那些已走过的点是可以达到汇点的。
- 解决方案(没想出来):如果不在搜索路径的中途判定,而是单独判断从某个点到汇点是否联通的话,这个判断本身又会消耗太多的时间。
尝试三:最短增广路径,广度优先
我还是决定看看别人的算法,于是我找到了这篇博客:网络最大流算法,并计划使用Edmonds-Karp算法,即每次寻找一条从源点到汇点的最短路径,以此更新边的剩余流量、最大流。
使用广度优先搜索策略可用来寻找最短路径,从源点开始,在搜索的同时,构建出一个层次网络,到达汇点时停止搜索。然后从汇点逆向一直走,就可以得到一条从源点到汇点的路径。(如果想得到最短路径,可以给层次网络中的每个点标上层号)
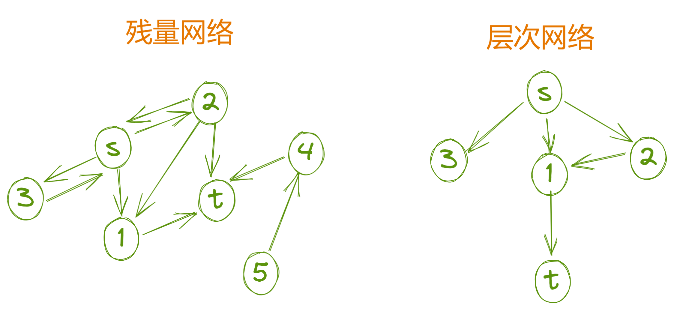
图中点2没有指向t是因为有一个点到达t时就可以停止搜索了。此时我们从t往回走,总能得到一条s与t之间的路径,它可能是:
t -> 1 -> s
t -> 1 -> 2 -> s
我们发现,在层次网络中往回走的过程中,每一步要么使所在层数降低,要么层数不变,但层次不会增大。(而如果你给每一点标记了层号,就可以限制每次都是向上一层走)
残量网络:原来的网络,每次找到路径后会更新网络中每条边的剩余流量,故称为残量网络。
相比深度优先搜索:即使你不要求最短路径,也总能以不太大的代价找到一条路径,而不会陷入局部的泥沼。
还是没ac
在自己对代码测试一番后,就觉得可以了,然而还是有三个测试点没过。测试数据下载下来发现是200个点,5000条边(数据中有重复的边)的那种,调试感觉无从下手,我至今没有找到问题出在哪。

记两个小bug
1. 数组越界
忘记使用数组下标是从1开始的了,因此数组大小应定义为nNum+1。

2. 写错变量名
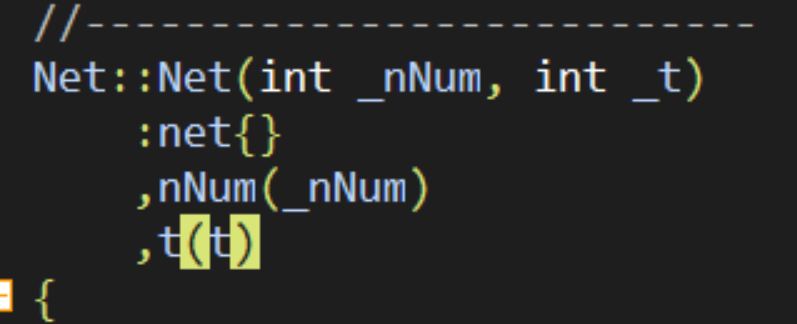
不是第一次,也不是第n次,是第n+1次了。初始化列表中应为t(_t)。
小结
在这个问题上花了好多时间,还是没得到一个好的结果。有时会有些后悔感,感觉那些时间花得不值得。我总喜欢了解一下算法大体思路后就自己去琢磨具体的细节和实现,而不愿意去阅读别人的源代码,好几次一个题的bug找很久。有时bug是思路上的,有时是写代码太粗心导致的错误。但是这样太花时间了。
最近从其它方面得到一些感受,多观察是有益的。
最后一个版本的代码(C++)
定义类与函数
#include<iostream>
#include<cstdio>
#include<climits>
#include<cstdlib>
#include<queue>
using namespace std;
const int Len = 201;
class Net
{
public:
int net[Len][Len];
int *road;
int iR;
long long sum;
int nNum;
int s;
int t;
Net(int _nNum, int _s, int _t);
void findRoad();
void upNet();
void forward();
};
//---------------------------
Net::Net(int _nNum, int _s, int _t)
:net{}
,nNum(_nNum)
,s(_s)
,t(_t)
{
iR = 0;
sum = 0;
road = new int[nNum]{};
}
//---------------------------
void Net::findRoad()
{
iR = 0;
int net2[Len][Len]{};//层次网络
bool pass[nNum + 1]{};//走过为true
queue<int> q;//辅助层次网络构建
q.push(s);
//pass[s] = 1;
//构建层次网络
while(1){
int front = q.front();
if(pass[front] == 1){
q.pop();
// 可能越界
if(q.empty()){
return;
}
front = q.front();
}
pass[front] = 1;
q.pop();
bool flag = 0;
for(int i = 1; i <= nNum; i++){
if(net[front][i] > 0 && pass[i] == 0){
net2[front][i] = net[front][i];
q.push(i);
if(i == t){
goto ROAD;
}
flag = 1;
}
}
if(flag == 0 && q.empty() == true){
break;
}
}
//得到从源点到汇点的路径
ROAD:
for(int i = 1, now = t; i <= nNum; i++){
if(net2[i][now] > 0){
road[iR++] = now;
if(i == s){
road[iR++] = i;
break;
}
now = i;
i = 0;
}
}
}
//---------------------------
void Net::upNet()
{
//1.找road最小值,更新最大流
int min(INT_MAX);
for(int i = 0; i <= iR - 2; i++){
if(net[road[i + 1]][road[i]] < min){
min = net[road[i + 1]][road[i]];
}
}
sum += min;
//2.更新net残量,建立反向边
for(int i = 0; i <= iR - 2; i++){
net[road[i + 1]][road[i]] -= min;
net[road[i]][road[i + 1]] += min;
}
}
//---------------------------
void Net::forward()
{
findRoad();
while(iR > 0){
upNet();
findRoad();
}
}
主函数
int main(){
int n = 2;
int m = 1;
int s = 1;
int t = 2;
cin >> n >> m >> s >> t;
Net netWork(n, s, t);
for(int i = 1; i <= m; i++){
int a = 0, b = 0, w = 0;
cin >> a >> b >> w;
netWork.net[a][b] = w;
}
netWork.forward();
printf("%lld", netWork.sum);
return 0;
}
类与函数的调试版本
IDLE的调试工具我用得不多,比较习惯于通过输出中间结果进行debug,这里记录了含输出点的代码。
#include<iostream>
#include<cstdio>
#include<climits>
#include<cstdlib>
#include<queue>
using namespace std;
const int Len = 201;
class Net
{
public:
int net[Len][Len];
int *road;
int iR;
long long sum;
int nNum;
int s;
int t;
Net(int _nNum, int _s, int _t);
void findRoad();
void upNet();
void forward();
};
//---------------------------
Net::Net(int _nNum, int _s, int _t)
:net{}
,nNum(_nNum)
,s(_s)
,t(_t)
{
iR = 0;
sum = 0;
road = new int[nNum]{};
}
//---------------------------
void Net::findRoad()
{
iR = 0;
int net2[Len][Len]{};//层次网络
bool pass[nNum + 1]{};//走过为true
queue<int> q;//辅助层次网络构建
q.push(s);
//pass[s] = 1;
//构建层次网络
while(1){
int front = q.front();
if(pass[front] == 1){
// test pop 已过点
// printf("pop %d\n", front);
//---------------------------end
q.pop();
// 可能越界
if(q.empty()){
return;
}
front = q.front();
}
pass[front] = 1;
//test pop
// printf("pop %4d\n", front);
//--------------------end
q.pop();
bool flag = 0;
for(int i = 1; i <= nNum; i++){
if(net[front][i] > 0 && pass[i] == 0){
net2[front][i] = net[front][i];
//pass[i] = 1; //改在出队时进行
//test push
// printf("push %4d\n", i);
//--------------------end
q.push(i);
if(i == t){
goto ROAD;
}
flag = 1;
}
}
if(flag == 0 && q.empty() == true){
break;
}
}
ROAD:
for(int i = 1, now = t; i <= nNum; i++){
//printf("ROAD i:%4d, now:%4d, e:%4d\n", i, now, net[i][now]);
if(net2[i][now] > 0){
road[iR++] = now;
//test ROAD
// printf("road:");
// for(int i = iR - 1; i >= 0; i--){
// printf("%4d", road[i]);
// }
// printf("\n");
//--------------------end
if(i == s){
//test t to road
//printf("to ROAD\n");
//------------------end
road[iR++] = i;
break;
}
now = i;
i = 0;
}
}
//test 层次网络
// printf("层次网络:\n");
// for(int i = 1; i <= nNum; i++){
// for(int j = 1; j <= nNum; j++){
// printf("%4d", net2[i][j]);
// }
// printf("\n");
// }
//--------------------end
//test ROAD
// printf("road:");
// for(int i = iR - 1; i >= 0; i--){
// printf("%4d", road[i]);
// }
// printf("\n");
//------------------end
}
//---------------------------
void Net::upNet()
{
//1.找road最小值,更新最大流
int min(INT_MAX);
for(int i = 0; i <= iR - 2; i++){
if(net[road[i + 1]][road[i]] < min){
min = net[road[i + 1]][road[i]];
}
}
sum += min;
//test min and sum
// printf("min:%d\n", min);
// printf("sum:%lld\n", sum);
//---------------------------end
//2.更新net残量,建立反向边
for(int i = 0; i <= iR - 2; i++){
net[road[i + 1]][road[i]] -= min;
net[road[i]][road[i + 1]] += min;
}
//test 残量
// printf("残量网络:\n");
// for(int i = 1; i <= nNum; i++){
// for(int j = 1; j <= nNum; j++){
// printf("%4d", net[i][j]);
// }
// printf("\n");
// }
//---------------------------end
}
//---------------------------
void Net::forward()
{
findRoad();
//test iR
// printf("iR:%4d\n", iR);
//---------------------------end
while(iR > 0){
upNet();
findRoad();
//test iR
// printf("iR:%4d\n", iR);
//---------------------------end
}
}
完