背包问题
- 1. 最基础的背包 —— 01背包 (必看)
- 1.1 分析
- 1.2 状态转移方程 和 边界条件
- 1.3 代码
- 1.3.1 代码模拟
- 1.4 空间复杂度的优化
- 1.4.1 错误的优化方式
- 1.4.2 正确的优化方式
- 1.5 终极版优化
- 总结
本文章参考自 B站 董晓算法
董晓算法
1. 最基础的背包 —— 01背包 (必看)

所谓的01背包问题就是每个物品放么放 0 次要么只能放 1 次,这就是01背包问题。
题目要求很简单,就是给你 几个物品,这几个物品有各自的重量(或体积)和价值,要求你在有限的背包内放下最大价值的物品选择。 看样例输入,就是 下面会给你 3 个物品 ,然后背包 总重量为 6,下面的 3 个物品 第一项是 重量 ,第二项是 价值。 可以得到当 选择
2 3 和 4 6 这个组合时,可以得到最大价值 9 。
动态规划分析法
1.确定状态变量(函数)
2.确定状态转移方程
3.确定边界条件
本题的 最大价值函数为 f(i,j),i 为物品的数量, j 为背包的容量
那么 设 函数 f [ i ] [ j ],表示前 i 件物品放入容量为 j 的背包的最大价值。
那么最终的最大价值就是物品数量 i 从 0 增长到 n ,背包容量 j 从 0 增长到 m 时的 f [ n ][ m ] 值。
注意这里的 “前 i 件物品”,它是状态转移的关键,即从上一个状态转移到下一个状态我们会如何做选择。
它也是我们保证 最终 f [ n ][ m ] 是最大价值的关键 !
1.1 分析
已知我们的状态变量函数是
f[i][j]
表示前 i 件物品放入容量为 j 的背包的最大价值
当背包容量为 j ,我们要考虑 第 i 件物品 能否放入 ? 是否放入 ?
以下w[i] 表示第i件物品的重量,v[i] 表示第 i 件物品的价值
1.如果当前背包的容量 j < w[ i ],则 f[ i ][ j ] = f[ i - 1][ j ]
解释 : 因为 第 i 件物品的重量大于当前背包的容量 j ,所以我们不放入它。
则 状态转移后 前 i 件物品 的价值和 它相同。
2.如果当前背包的容量 j >= w[i] ,则能放入它,但是要比较代价
(1) 如果第 i 件物品不放入背包,则还是 f[ i ][ j ] = f[ i - 1][ j ]
(2)如果第 i 件物品放入背包,则 f[ i ][ j ] = f[i - 1][ j - w[ i ]] + v[ i ];
在放与不放中选择最优的选择,是我们要考虑的。
解释:(1) 中,因为我们不放入背包,所以状态转移后,和前 i 件的状态相同。
(2)中,如果 第 i 件物品 放入背包 ,则背包容量还剩 j - w[ i ] , 所以要取前 i - 1件物品放入背包剩余容量 j - w[i]所获得的最大价值
f[ i - 1 ][ j - w[ i ] ]
我们这时的目的就是在放与不放这两种选择中,选择最优的选择。
看个例子

1.2 状态转移方程 和 边界条件
经过上面的分析,我们可以得到这样一个图
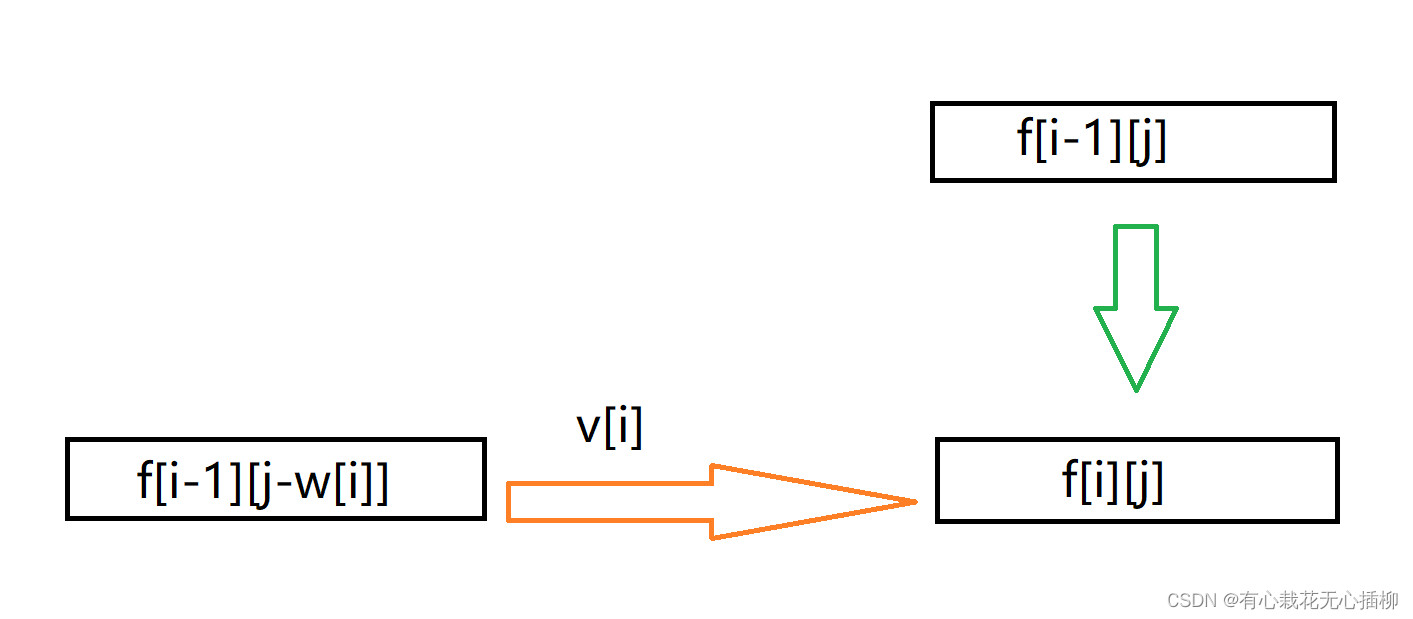
一种是当前状态和上一状态相同,放在表格中,就是直接从上一行的位置直接移下来。
一种是当前状态和上一状态不同,加了一个价值v[i],放在表格中,就是相差了 w 列,再在那个单元格中加上 v[i]
那么,我们可以得到我们的状态转移方程
f[i][j] = f[i - 1][j] 当(j < w[i])时
f[i][j] = max(f[i-1][j],f[i -1][j - w[i]] + v[i]) 当(j >= w[i])时
第二个式子就是取不放入背包和放入背包两种情况的最大值。
边界条件:
f[i][j] = 0
初始化为0,也就是一开始都没有放入背包
1.3 代码
for(int i = 1;i <= n;i++) // 物品 i
{
for(int j = 1;j <= m;j++) // 容量 j
{
if(j < w[i]) //背包容量小于第i件物品的重量
{
f[i][j] = f[i - 1][j];//就复制上一行的价值
}
else//否则就取放入和不放入的最大值
{
f[i][j] = max(f[i-1][j],f[i - 1][j - w[i]] + v[i]);
}
}
}
我们是从 1 开始循环,理由很简单,就是 第 0 件物品 和 背包容量为 0 时,价值都是 0 ,我们没必要从 0 开始循环。
1.3.1 代码模拟
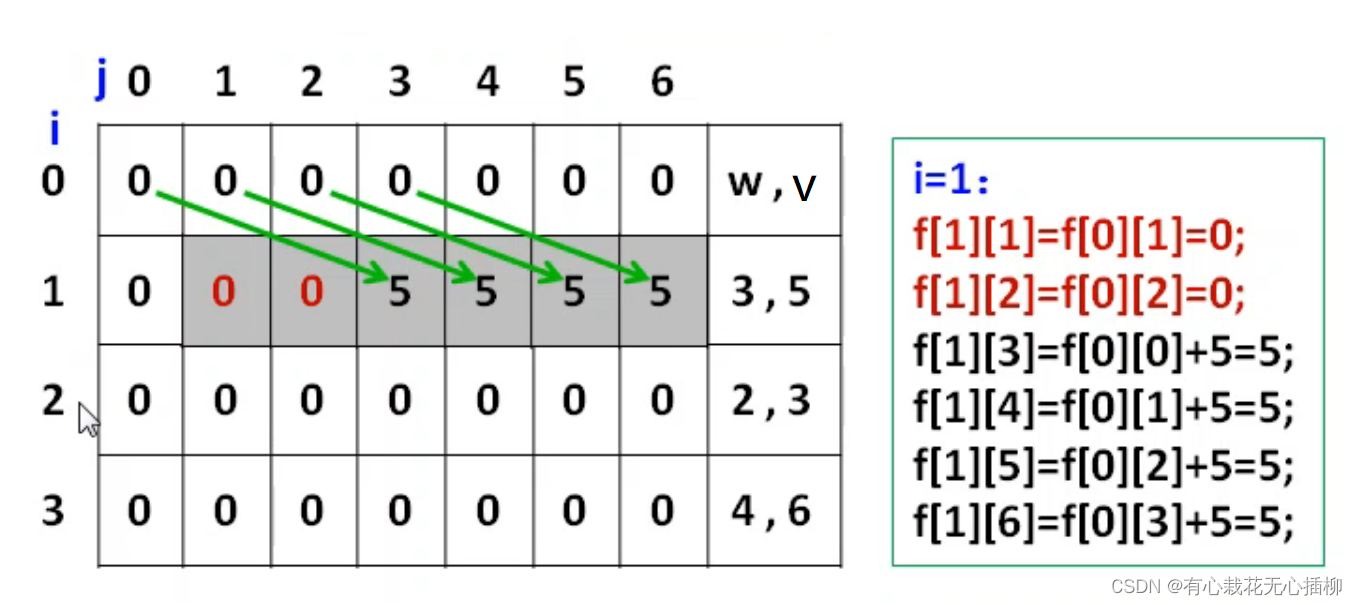
当物品重量为 3 ,价值为 5
放入第一件物品 也就是是 i = 1,时,我们观察 随着 j 变化发生了什么
j = 1,放不下,直接从上一行复制值
j = 2,放不下,直接从上一行复制值
j = 3,可以放进来,价值为 5 ,f[1][3] = f[0][0] + 5 = 5
j = 4,可以放进来,价值为5, f[1][4] = f[0][1] + 5 = 5
j = 5,可以放进来,价值为5,f[1][5] = f[0][2] + 5 = 5
j = 6,可以放进来,价值为5,f[1][6] = f[0][3] + 5 = 5
我们可以看到,当 物品可以放进来时该单元格的值,可以从上一行列数相差 w 的单元格来推出。
我们继续模拟
放入 i = 2 时,也就是放入第 2 件物品时,我们观察随着 j 的变化发生了什么
j = 1 时,放不下 f[2][1]=f[1][1] = 0
j = 2 时,可以放下,价值为 3 f[2][2]=f[1][0] + 3 = 3
j = 3 时,可以放下,但是是直接从上一行拷贝下来
为什么可以放下却是直接从上一行拷贝下来?
因为我这里能放下时,只能放下价值为 3 的物品,那不如直接放价值更大的5,
所以直接拷贝下来
代码里的 max 函数可以体现出来
j = 4 时,可以放下,但是是直接从上一行拷贝下来
j = 5时,可以放下,第一件物品和第二件物品,价值加起来为 8
j = 6时,同理
可以看到,当可以放进来单元格时的值,同样可以利用上一行列数相差为 w 的单元格来推出 或者 上一行的值来推出
我们继续模拟
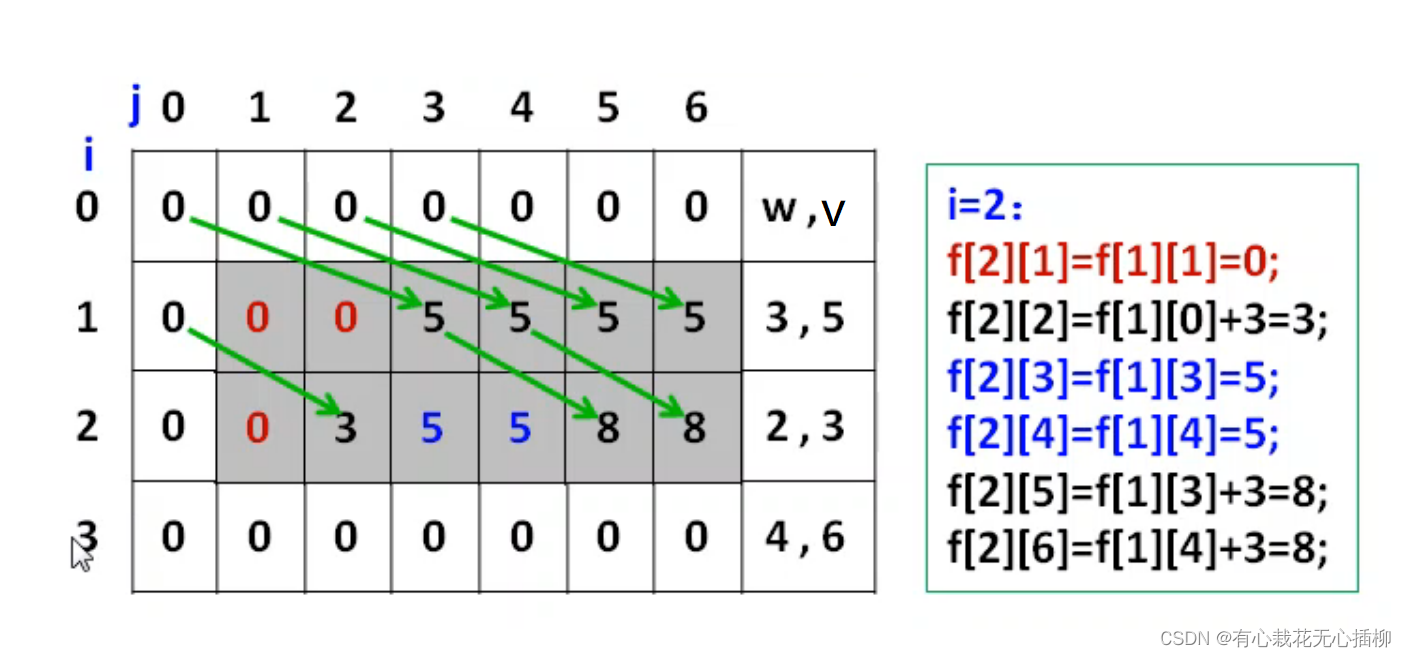
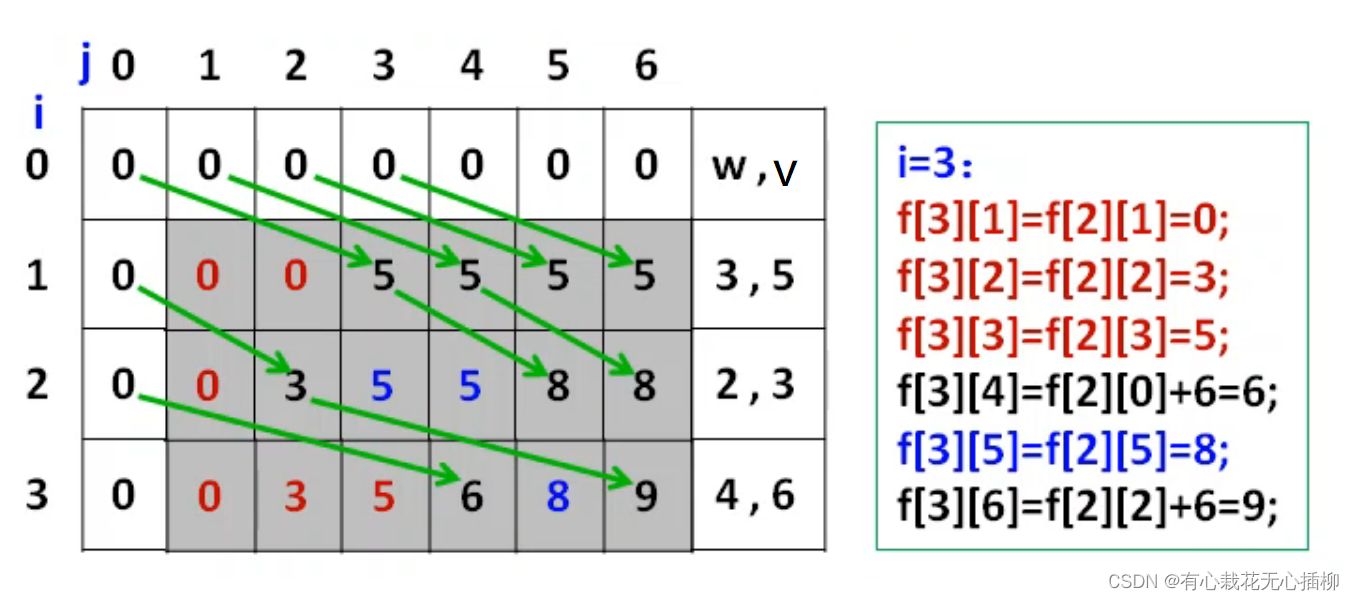
当 i = 3 ,也就是放入第三件物品时,我们观察随着 j 的变化发生了什么?
j = 1,时,放不下,直接从上一行复制值 f[3][1]= f[2][1]=0
j = 2 时,只能放下上次的第二件物品,所以最大值就是第二件物品的价值,直接复制下来
f[3][2]= f[2][2]=3;
j = 3时,可以放下 第二件物品 。f[3][3] = f[2][3] = 5,直接从上一行复制下来
j = 4时,可以放下 第三件物品,f[3][4]=f[2][0] + 6=6
j = 5时,我们不放入第三件物品,因为价值不如放入第一件物品和第二件物品的价值
所以我们取最大价值 f[3][5]=f[2][5]=8
j=6时,可以判断出最大价值为第二件物品加上第三件物品,从上一行列数相差为 w 的单元格推出
f[3][6]=f[2][2]+6=9
这样,我们的最大价值就是 f[3][6]=9
1.4 空间复杂度的优化
再来回顾以下这个代码,是不是豁然开朗
for(int i = 1;i <= n;i++) // 物品 i
{
for(int j = 1;j <= m;j++) // 容量 j
{
if(j < w[i]) //背包容量小于第i件物品的重量
{
f[i][j] = f[i - 1][j];//就复制上一行的价值
}
else//否则就取放入和不放入的最大值
{
f[i][j] = max(f[i-1][j],f[i - 1][j - w[i]] + v[i]);
}
}
}
这段代码时间复杂度为 o(nm),基本上不能再优化了
但是空间复杂度为 o(nm),空间复杂度却可以再优化一下
由二维降为一维
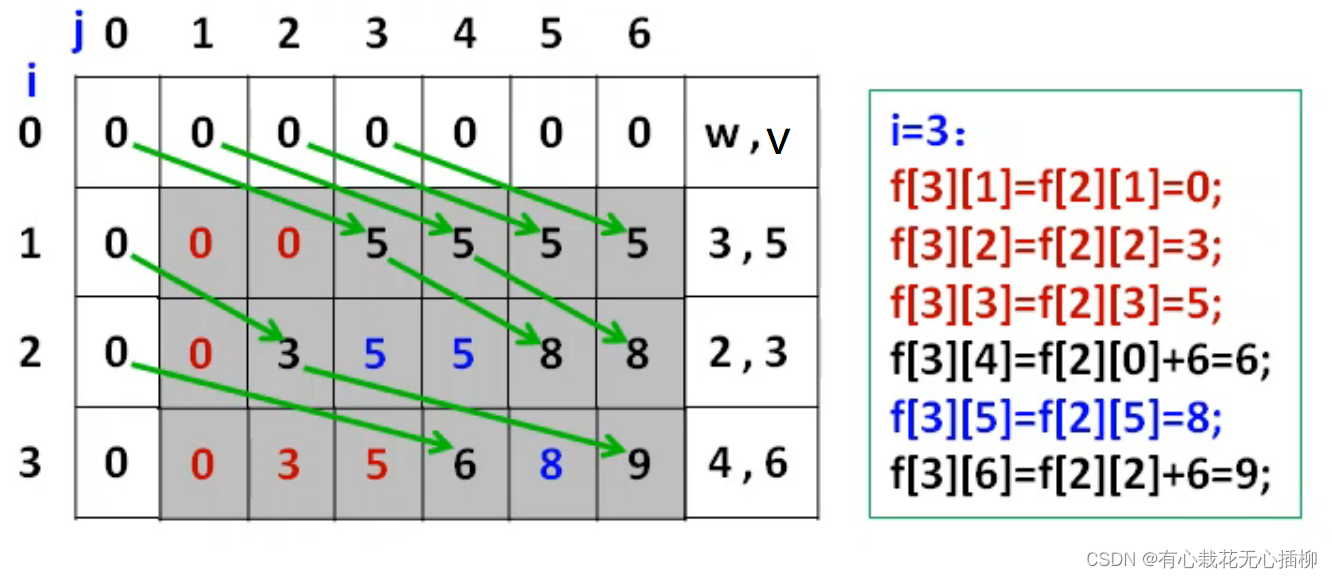
通过刚才代码模拟我们可以发现,每次第i行都是从上一行更新数据,那么当第i行数据更新完成后,上一行是不是可以不用保存了?
1.4.1 错误的优化方式
让一维数组f[j] 只记录一行数据,让j值顺序循环,循环更新f[j]的值会怎么样
来看一下这段错误的代码
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
if(j < w[i])
{
f[j] = f[j];
}
else
{
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
}
我们模拟一下
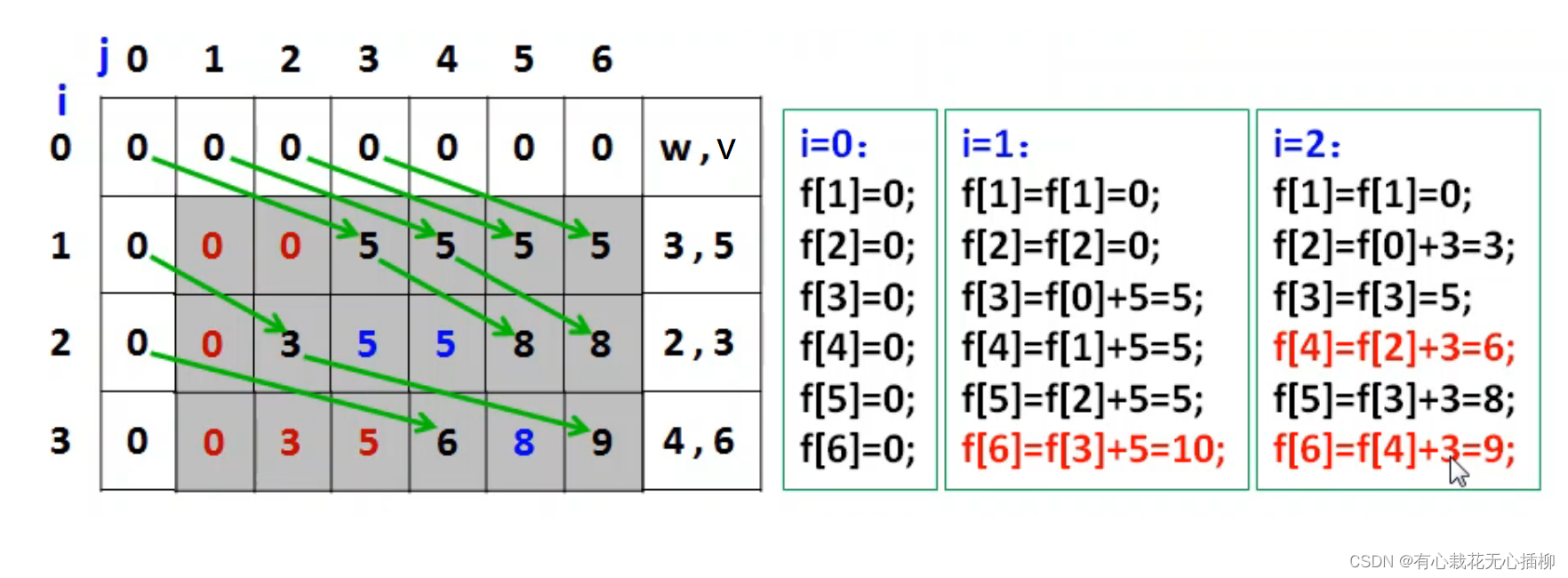
当 i = 1,也就是放入第 i 件物品时,我们管擦随着j变化发生了什么?
j = 1,放不下 f[1] = 0;
j = 2,放不下 f[2] = 0;
j = 3,可以放下 f[3] = f[0] + 5 = 5;
j = 4,可以放下 f[4] = f[1] + 5 = 5;可是这里的f[1]是我们本行就已经更新值了,拿本行的值继续更新会有什么问题?
j= 5,可以放下 f[5] = f[2] + 5 = 5 ;这里同理,f[2]是我们本行更新的值
问题来了
j = 6,f[6] = f[3] + 5 = 10 出错了,原因就是 f[3] 的值是在我们本行更新的,这样子顺序更新后面肯定会出错!
因为f[j]是顺序循环,f[j - w[i]] 会先于 f[j]更新,那么我们用 新值f[j - w[i]] 的值取更新 f[j],就会出错
1.4.2 正确的优化方式
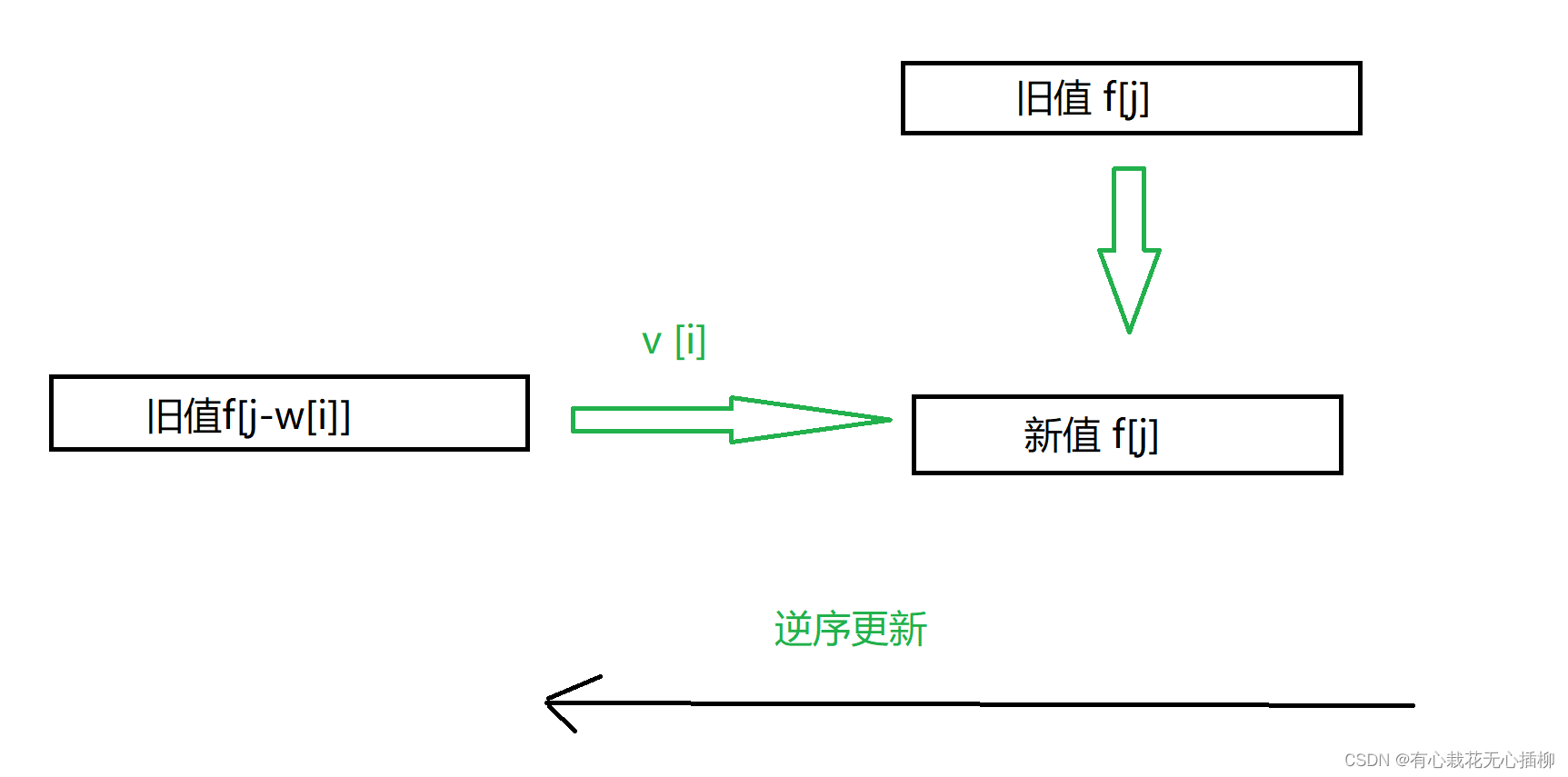
既然 f[j] 顺序更新不行,那我们就反过来,逆序更新嘛
让 f[j] 逆序循环,让 f[j] 先于 f[j - w[i]] 更新,用旧值 f[j - w[i]] 去更新 f[j]
旧值 f[j - w[i]] 相当于上一行的数,所以优化思路正确
for(int i = 1;i <= n;i++)
{
for(int j = m;j >= 1 ;j--)
{
if(j < w[i])
{
f[j] = f[j];
}
else
{
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
}
我们模拟一下这段代码
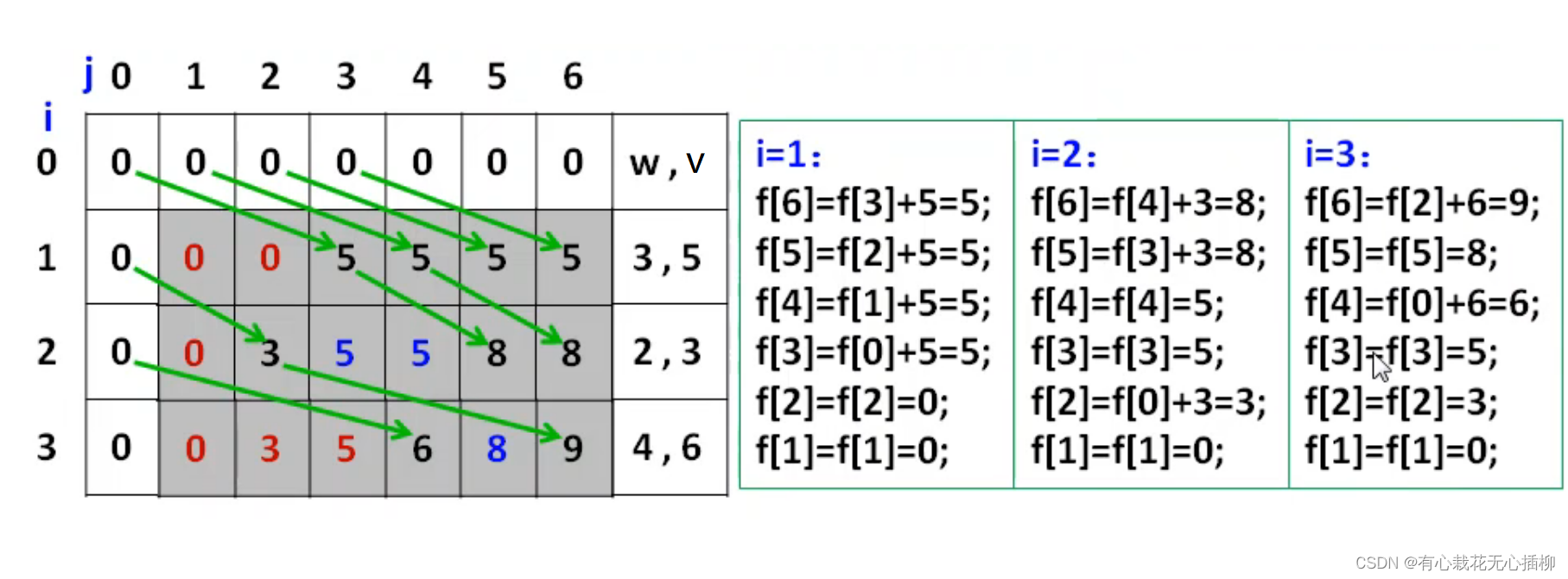
当 i = 1,放入第 1 件物品时,我们观察随着 j 变小,会发生什么?
j = 6时,可以放下,f[6] = f[3] + 5 = 5
j = 5时,可以放下,f[5] = f[2] + 5 = 5
j = 4时,可以放下,f[4] = f[1] + 5 = 5
j = 3时,可以放下,f[3] = f[0] + 5 = 5 ,可以看到,我们f[3] 后面才更新,避免了顺序更新那样提前更新导致后面的数据出错的情况
j = 2,放不下 f[2] = f[2] = 0
j = 1, 放不下 f[1] = f[1] = 0
当 i = 2 ,放入第 2 件物品时,
j = 6 时,可以放下,f[6] = f[4] + 3 = 5 + 3 = 8;
以此类推,就不再继续模拟了
因为 f[j] 是逆序循环,f[j] 会先于 f[j - w[i]] 更新,也就是说,用旧值,f[j - w[i]] 去更新 f[j],
相当于用上一行的 f[j - w[i]] 去更新 f[j],所以思路正确
这里的 f[j] 循环一遍,值就会滚动更新一遍,所以 f[j] 也称为滚动数组
我们用了滚动数组,把空间复杂度从二维降到了一维
1.5 终极版优化
我们看一下之前的代码看看哪里可以优化
for(int i = 1;i <= n;i++)
{
for(int j = m;j >= 1 ;j--)
{
if(j < w[i])
{
f[j] = f[j]; //这里可以优化
}
else
{ //如果上面的if 省略 这里的j - w[i] 可以出现负数,导致出错
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
}
经过几番周折,终于磨练出了下面这份近乎完美的代码
for(int i = 1;i <= n;i++) // 物品 i
{ // 把j的下限改为 w[i]
for(int j = m;j >= w[i];j--) // 容量 j
{
f[j] = max(f[j],f[j - w[i]] + v[i]);
}
}
总结
动态规划的题目分析思路
1.确定状态变量(函数)
2.确定状态转移方程
3.确定边界条件
4.确定递推顺序
背包问题状态转移方程
f[j] = max(f[j],f[j - w[i]] + v[i])
这个方程非常重要,一定要记住!