1.题目描述:
给定n阶台阶的楼梯,一次能跳m阶问跳到楼顶有多少种方法?假设m可以是1~9任意一种,weight[i] = {1,2,3,4,5,6,7,8,9}
解法:
1.五步曲:
①将本题转换成背包问题---即给定容量为n的背包,求放满这个背包一共有多少种方法,每个物品可以重复使用。
②dp[j]表示,容量为j,有dp[j]种方法填满
③递推公式:dp[j] += dp[j-weight[i]]
④初始化:因为根据前面的值获得的,所以初始化dp[0] = 1---即容量为0,不填充也是一种方法,否则的话根据递推公式所有的值都会是0.非0位置的初始化=?因为要和本身累加和,所以初始化为0。
⑤遍历顺序:因为是完全背包问题,所以正序遍历背包。那么先遍历背包还是先遍历物品呢?因为我们要求的是多少种方法,即121和122是不一样的,故求的是排列数,故先遍历背包再遍历物品。
2.步骤:
①创建dp数组,长度为n+1
②初始化dp数组,dp[0] = 1,其余位置为0
③遍历:for(背包正序遍历,从0开始到n){
for(物品,从0开始到weight[i].length){
if(j >= weight[i]){
dp[j] += dp[j-weight[i]];}
}
}
④最后返回dp[n]
下面为代码(java):


2.题目链接:322. 零钱兑换
题目描述:
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
解法:
1.五步曲:
①将本题转化成背包问题---即装满容量为amount的背包,求最少装物品的个数。
②dp[j]表示的就是装满容量为j的背包,最少装dp[j]个物品
③递推公式:dp[j] = ?假如背包中装了一个物品重量为coins[i],那么此时的dp[j] = dp[j-coins[i]] + 1,但是对于每一个i值都有一个dp[j],而我们要求其最小值,所以dp[j] = min(dp[j-coins[i]] + 1, dp[j])
④初始化:根据递推公式,当前值是根据前面的值求出来的,所以要初始化dp[0] = ?即dp[0] = 0,装满背包容量为0的背包需要最少装物品的个数为0.
对于非0处的值应该初始化为多少呢?根据递推公式,要和本身的值取最小,所以我们要初始化成最大值---即Integer.MAX_VALUE。
⑤遍历顺序:因为我们要求的是硬币个数,所以不管是有序的还是无序的,个数都是一样,所以先遍历背包或者先遍历物品都是可以的。而同时每个硬币可以用无限次,所以这是个完全背包问题,所以要正序遍历背包。
⑥最后返回dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount]
⑦需要注意的是在写递推公式的上方要加上if(dp[j - coins[i]] != MAXVALUE) ,因为如果等于的话,递推公式就相当是dp[j] = dp[j]没有意义。
2.步骤:
①创建dp数组,长度为amount+1
②初始化dp数组,dp[0] = 1,非0位置初始化为Integer.MAX_VALUE
③遍历顺序:先遍历背包还是先遍历物品都可以(因为求的是个数),正序遍历背包。
if(dp[j-coins[i]] != Integer.MAX_VALUE){dp[j] = min(dp[j],dp[j-coins[i]] + 1)}
④最后返回 dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount] --- 即如果构不成amount就返回-1,构成了就返回需要的最少硬币个数。
下面为代码(java):

3.题目链接:279. 完全平方数
题目描述:
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
解法:
1.五步曲:
①将其转化成背包问题---给定容量为n的背包,求将其装满的最少物品数目。
②dp[j]的含义就是将容量为j的背包装满,需要的少完全平方数的数量。
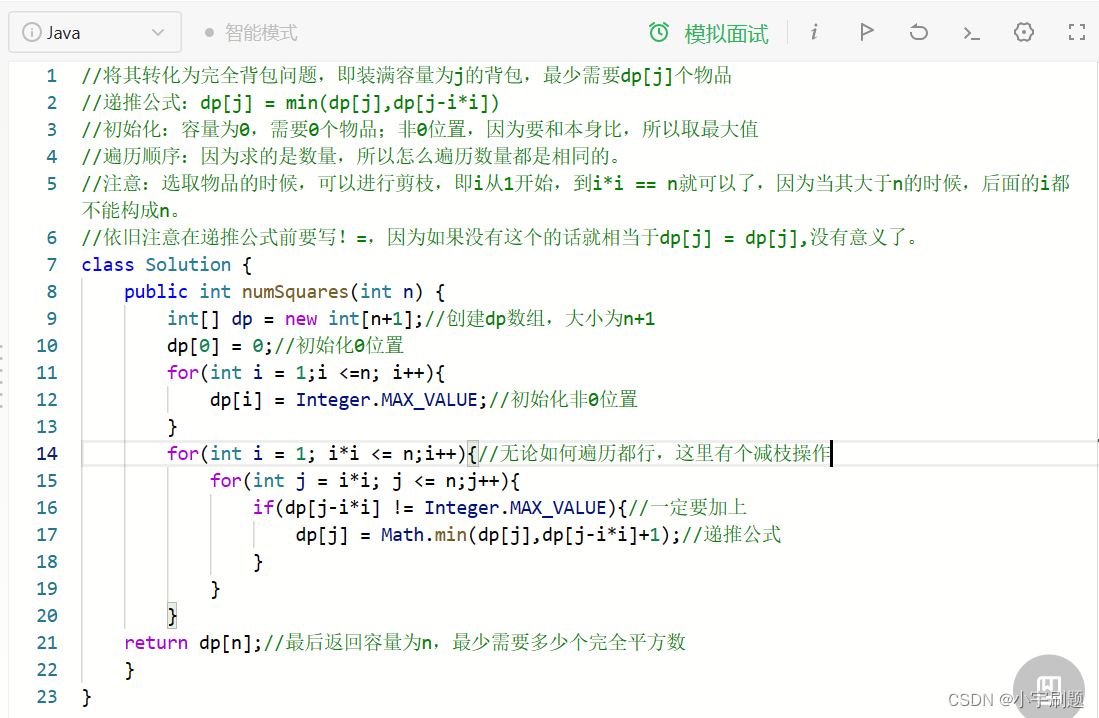
③递推公式:dp[j] = min(dp[j], dp[j - i *i]+1)
④初始化:依旧要初始化为dp[0] = 0;非0位置:因为和本身比要取最小,所以取最大Integer.MAX_VALUE
⑤遍历顺序:因为求的是个数,所以不论是求组合数还是排列数,个数都是一致的,所以先遍历物品还是先遍历背包都可以。因为每一个完全平方数可以用多次,所以是完全背包,所以要正序遍历背包。
⑥最后返回dp[n]
⑦要注意的是在遍历物品的时候有减枝操作,即for(i = 1; i*i<=n;i++)因为如果i的平方大于n了,那么n肯定不能由i的方法构成。
2.步骤:
①创建dp数组,长度为n+1
②初始化:dp[0] = 0;非0处初始化为最大值
③遍历:for(i=1;i*i <= n;i++){
for(j = i*i; j <=n;j++){
if(dp[j-i*i] != Integer.MAX_VALUE){
dp[j] = min(dp[j], dp[j-i*i]+1);}
}
}
④最后return dp[n]
下面为代码(java):
4.总结:
①三题都是物品可以重复使用,所以都是完全背包问题,背包都要正序遍历。
②爬楼梯进阶 --- 求的是方法数目,即排列数,因为不同的数字排列是不同的方法。所以要先遍历背包再遍历物品。
③零钱兑换 --- 求的是最少个数,所以无论求的是排列数还是组合数个数都是相同的,所以先遍历背包还是先遍历物品都可以。递推公式:dp[j] = min(dp[j], dp[j-coins[i]] + 1)
④完全平方和 --- 求的是最少个数,所以哪个先遍历都可以。递推公式:dp[j] = min(dp[j], dp[j-i*i] + 1)
⑤在求最小值的时候初始化为最大值,求最大值的时候初始化为合理的最小值。