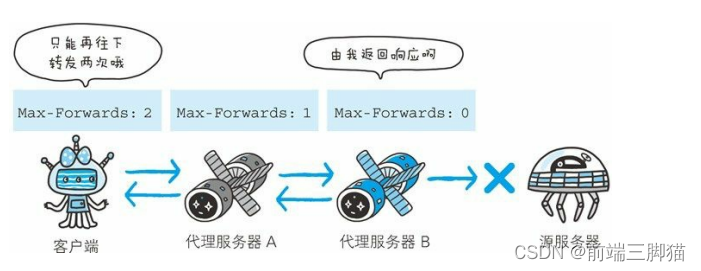
本文以取 (bs, n, n) 张量的右上三角阵并展平为向量 (bs, n*(n+1)//2)) 为例，展示如何用 taichi 编写深度学习算子。

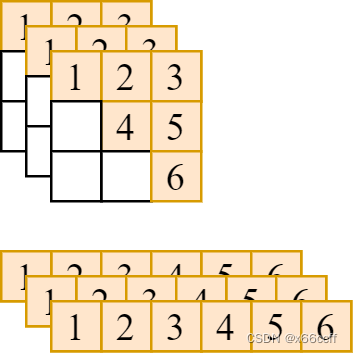
如图，要把形状为 $(bs,n,n)$ 的张量，转化为 $(bs,\frac{n(n+1)}{2})$ 的向量。我们先写一个最简单的最慢的纯 python 循环实现方法

纯 python for 循环

def get_tensor_up_right_tri_slow(t):
    # t shape (bs, n, n)
    # out shape (bs, n*(n+1)//2)
    out = torch.zeros(t.shape[0], t.shape[1]*(t.shape[1]+1)//2)
    n = t.shape[1]
    # k = i*n + j - i*(i+1)//2
    for b in range(t.shape[0]):
        # 遍历右上三角阵，包括主对角线
        for i in range(t.shape[1]):
            for j in range(i, t.shape[1]):
                k = i*n + j - i*(i+1)//2
                out[b, k] = t[b, i, j]
    return out

可想而知，三层 python for 循环，必然是极慢的了。

转化为 taichi

在此基础上，稍微做一些修改，就可以得到我们的 taichi 版本函数

import taichi as ti

ti.init(arch=ti.gpu)

@ti.kernel
def get_tensor_up_right_tri(t: ti.types.ndarray(ndim=3, dtype=ti.f32), out: ti.types.ndarray(ndim=2, dtype=ti.f32)):
    # t shape (bs, n, n)
    # out shape (bs, n*(n+1)//2)
    n = t.shape[1]
    for b, i, j in t:
        # 遍历右上三角阵，包括主对角线
        if i <= j:
            k = i*n + j - i*(i+1)//2
            out[b, k] = t[b, i, j]

taichi 支持同时遍历多层循环，将三层循环改为一层循环后，和 python for 循环版本基本没有什么差别。taichi 将此函数转化为 CUDA 版本进行加速，从而提高运算速度。