机器学习实战--梯度下降法进行波士顿房价预测

news2024/11/13 8:58:37

前言： Hello大家好，我是Dream。 今天来学习一下如何使用机器学习梯度下降法进行波士顿房价预测，这是简单的一个demo，主要展示的是一些小小的思路~

本文目录：

一、波士顿房价预测
- 1.全部的数据可视化
- 2.地理数据可视化
- 3.房价和人口及位置数据可视化
- 4.所有相关数据的可视化
- 5.房价和收入的可视化
- 6.房价预测的线性回归模型训练
- - 梯度下降法
二、完整代码
- 1.正规方程
- 2.梯度下降法
源工程文件

一、波士顿房价预测

sklearn提供给我们两种实现的API，可以根据选择使用：
正规方程
sklearn.linear_model.LinearRegression()
梯度下降法
sklearn.linear_model.SGDRegressor(）

1.全部的数据可视化

data.hist(bins=50, figsize=(20, 15))

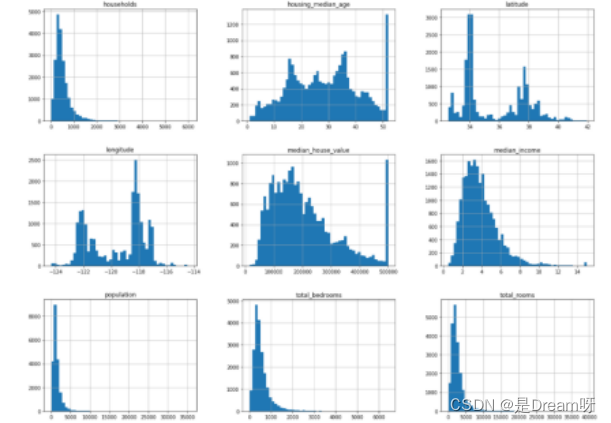
在这里插入图片描述

2.地理数据可视化

data.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4);

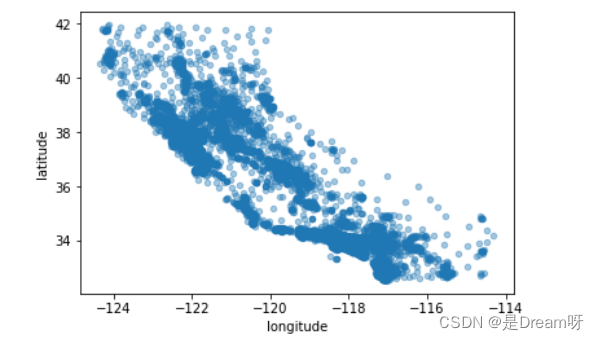
在这里插入图片描述

3.房价和人口及位置数据可视化

data.plot(kind="scatter", x="longitude", y="latitude", alpha=0.6,
    s=data["population"]/100, label="population", figsize=(11,8),
    c="median_house_value", cmap=plt.get_cmap("jet"))

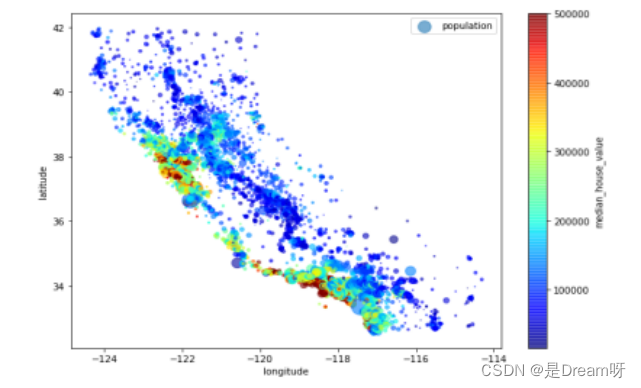
在这里插入图片描述

4.所有相关数据的可视化

features = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[features], figsize=(20, 15));

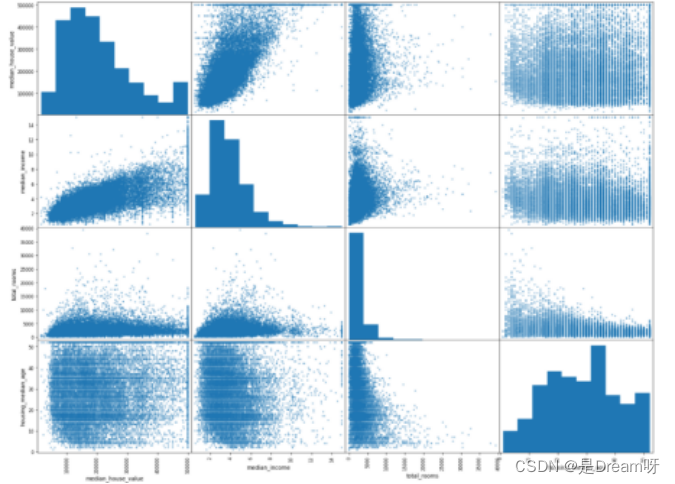
在这里插入图片描述

预测median_house_value最相关的特征是median_income。

5.房价和收入的可视化

data.plot(kind="scatter", x="median_income", y="median_house_value", alpha=0.4);

最后得到和房价最相关的是收入数据
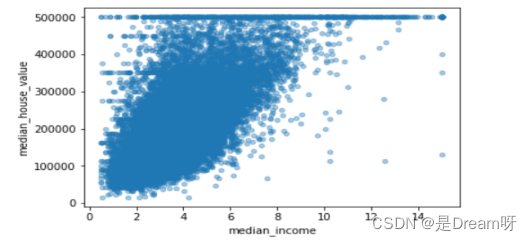
在这里插入图片描述

6.房价预测的线性回归模型训练

梯度下降法

def test():
m = 10000 
x = np.random.normal(size=m)
    X = x.reshape(-1, 1)
y = 4. * x + 3. + np.random.normal(0, 3, size=m)

    X_train, X_test, y_train, y_test = train_test_split(X, y)
    standardscaler = StandardScaler()
    standardscaler.fit(X_train)
x_train_standard = standardscaler.transform(X_train)

    lrg = LinearRegression()
    # lrg.fit_gd(x_train_standard, y_train, eta=0.001, n_iters=1e6)
    lrg.fit_sgd(x_train_standard, y_train)

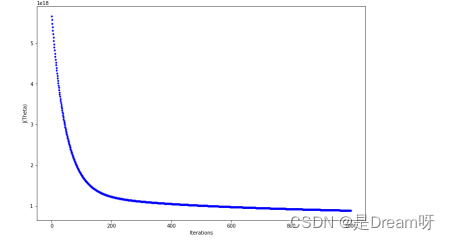
在这里插入图片描述

二、完整代码

1.正规方程

def linear_model1():
    """
    线性回归:正规方程
    :return:None
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(正规方程)
    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

    return None

2.梯度下降法

def linear_model2():
    """
    线性回归:梯度下降法
    :return:None
    """
    # 1.获取数据
    data = load_boston()

    # 2.数据集划分
    x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)

    # 3.特征工程-标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.fit_transform(x_test)

    # 4.机器学习-线性回归(特征方程)
    estimator = SGDRegressor(max_iter=1000)
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 5.1 获取系数等值
    y_predict = estimator.predict(x_test)
    print("预测值为:\n", y_predict)
    print("模型中的系数为:\n", estimator.coef_)
    print("模型中的偏置为:\n", estimator.intercept_)

    # 5.2 评价
    # 均方误差
    error = mean_squared_error(y_test, y_predict)
    print("误差为:\n", error)

    return None