首先，fmt.Sprintf("%.2f")使用的是banker rounding 而不是四舍五入，banker rounding 的定义如下（来自百度百科）：

1.要求保留位数的后一位如果是4，则舍去。例如5.214保留两位小数为5.21。

2.如果保留位数的后一位如果是6，则进上去。例如5.216保留两位小数为5.22。

3.如果保留位数的后一位如果是5，而且5后面不再有数，要根据应看尾数“5”的前一位决定是舍去还是进入: 如果是奇数则进入，如果是偶数则舍去。例如5.215保留两位小数为5.22； 5.225保留两位小数为5.22。

4.如果保留位数的后一位如果是5，而且5后面仍有数。例如5.2254保留两位小数为5.23，也就是说如果5后面还有数据，则无论奇偶都要进入。

按照四舍六入五成双规则进行数字修约时，也应像四舍五入规则那样，一次性修约到指定的位数，不可以进行数次修约，否则得到的结果也有可能是错误的。

%.2f表示保留两位小数，在实际测试中出现问题，如：

fmt.Sprintf("%.2f", 0.495) 得到 0.49 而不是 0.5

fmt.Sprintf("%.2f", 0.475) 得到 0.47 而不是 0.48 等

为了了解这个问题，需要先了解golang 保存浮点数的方式，在fmt.Sprintf("%.2f")的计算中 golang 使用strconv.decimal 表示浮点数，其结构如下：

type decimal struct {
    // 以[]byte形式表示的浮点数所有位
    d     [800]byte // digits, big-endian representation
    // 有效的位数，decimal.d 可能有很多位，但大于decimal.nd 的位数都是无效的，不会被使用
    nd    int       // number of digits used
    // 小数点所在的位数
    dp    int       // decimal point
    neg   bool      // negative flag
    trunc bool      // discarded nonzero digits beyond d[:nd]
}

具体原因需要查看fmt.Sprintf的源码，追到如下的调用栈：

strconv.shouldRoundUp (decimal.go:347) strconv
strconv.(*decimal).Round (decimal.go:358) strconv
strconv.bigFtoa (ftoa.go:184) strconv
strconv.genericFtoa (ftoa.go:154) strconv
strconv.AppendFloat (ftoa.go:54) strconv
fmt.(*fmt).fmtFloat (format.go:496) fmt
fmt.(*pp).fmtFloat (print.go:408) fmt
fmt.(*pp).printArg (print.go:666) fmt
fmt.(*pp).doPrintf (print.go:1122) fmt
fmt.Sprintf (print.go:219) fmt

在这里 strconv.shouldRoundUp 的源码如下：

// If we chop a at nd digits, should we round up?
func shouldRoundUp(a *decimal, nd int) bool {
    if nd < 0 || nd >= a.nd {
        return false
    }
    if a.d[nd] == '5' && nd+1 == a.nd { // exactly halfway - round to even
        // if we truncated, a little higher than what's recorded - always round up
        if a.trunc {
            return true
        }
        return nd > 0 && (a.d[nd-1]-'0')%2 != 0
    }
    // not halfway - digit tells all
    return a.d[nd] >= '5'
}

这里传入的nd是rounding 后的有效位，而a.nd是当前浮点数的有效位，第六行的逻辑是，如果目标有效位的最后一位是5，且（目标有效位+1 == 当前浮点数的有效位），则使用banker rounding。这里实际上就是检查这个数是否是x.xxxx50000 这种严格等于 （精度/2）的情况。如果第六行为false 则使用标准的四舍五入

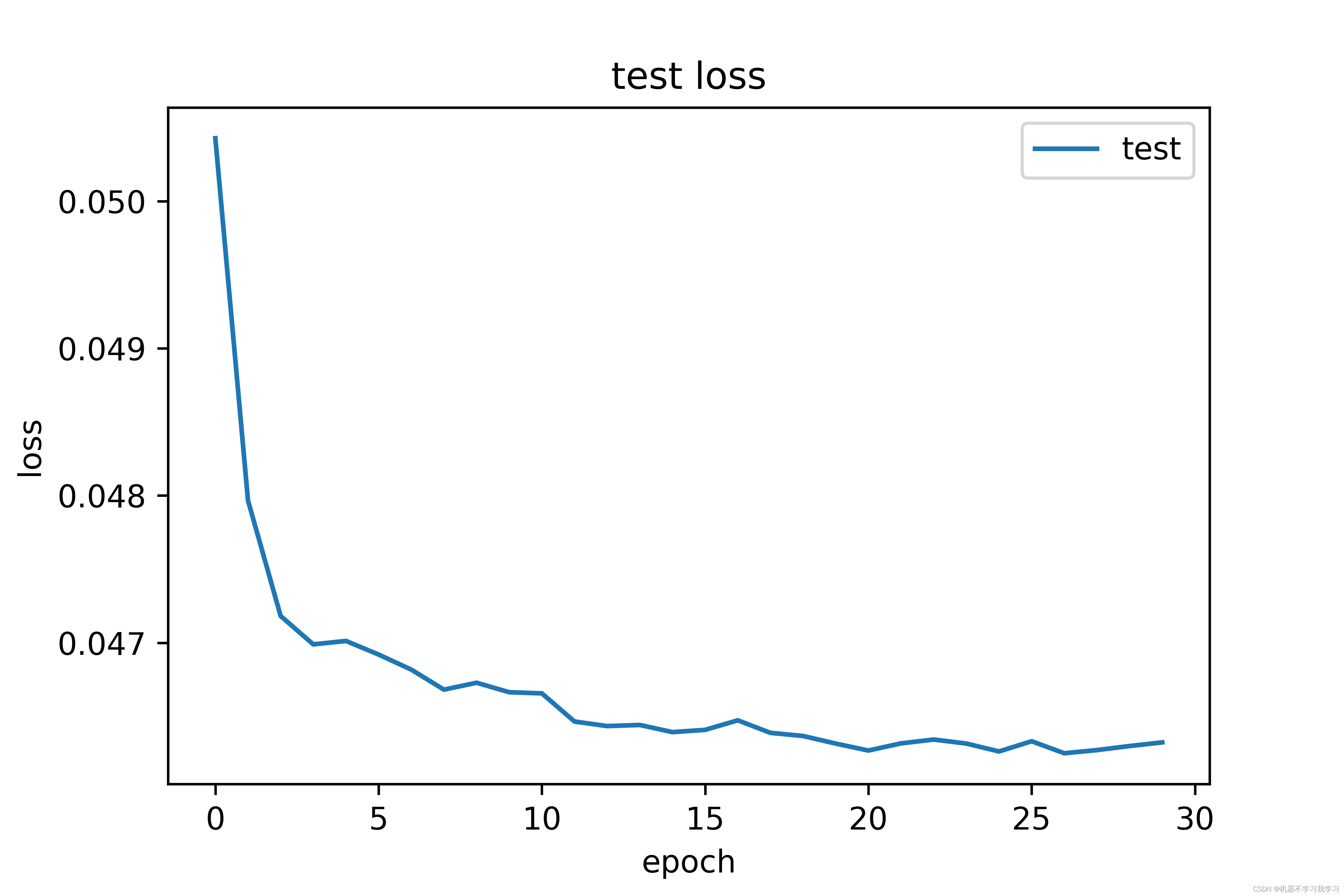
但是由于浮点数表示误差的问题，实际情况又有些差距，比如在fmt.Sprintf("%.2f", 0.495) 中，浮点数0.495无法被精确表达为二进制，所以实际上使用的值会有误差：

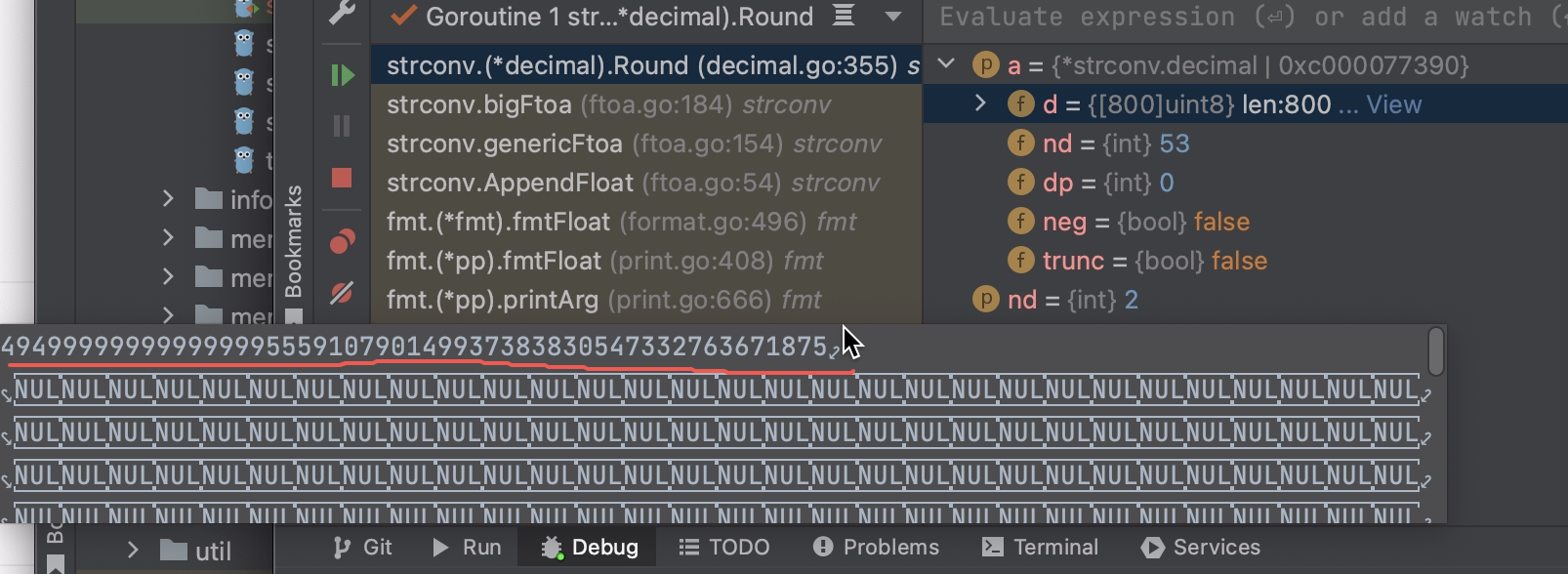
可以看到图中0.495被表示为49499999999999999555910790149937383830547332763671875 且 nd=53，即使用最多的有效位最大限度地接近实际值。此时做shouldRoundUp中的判断 （a.d[nd] == '5' && nd+1 == a.nd）就会得到false，从而对这个值进行四舍五入，又因为49499999999999999555910790149937383830547332763671875 应当使用“四舍”，所以会得到0.49 而不是 0.5。所以这里0.495看似应该使用banker rounding，实际上因为浮点数的表示误差而使用了四舍五入，并且采取了“四舍”，0.475也是同样的原理得出0.47。

需要注意，0.505会得到0.5不是因为正确地使用了banker rounding，而是因为0.505在表示中因误差而大于原值（0.505），从而采取了四舍五入中的“五入”，依然没有采取banker rounding

只有当原值可以被浮点数完美表示时才会采取banker rounding，如0.125可以按IEEE 754 标准表示为0011111111000000000000000000000000000000000000000000000000000000，不会有任何误差，此时会正确地使用banker rounding 得出0.12