文章目录
- lec1
- ML和RL之间的区别
- 几种RL分类
- current challenges
- lec4
- markov chain
- markov decision process
- partially observed markov decision process
- RL's goal
- Q & A
lec1
ML和RL之间的区别
| ml | rl |
|---|---|
| iid data | 数据不iid,前面的数据会影响future input |
| 训练时有确定的groundtruth | 只知道succ/fail,不知道具体的label |
| supervised learning需要人类给label,但是reinforcement learning可以用data给label是success, fail这样的 |
rl很长一段时间被feature困扰,不知道怎么选择feature更适合policy/value function,用deep RL可以解决feature的问题
几种RL分类
inverse reinforcement learning:learning reward functions from example
unsupervised learning:learning from obsering the world
meta-learning/transfer learning:learning to learn,根据历史的经验去学习
current challenges
- 人类学习很快,但DRL很慢
- human reuse past knowledge,RL用transfer learning
- 不知道reward function怎么设计
- 不知道role of prediction怎么设计
lec4
markov chain
定义:
M
=
{
S
,
T
}
M = \{S,T\}
M={S,T}
其中:
- S S S是state
- T T T是transition operator,假设 μ t \mu_t μt是一个prob vector,则有: μ t , i = p ( s t = i ) \mu_{t,i} = p(s_t=i) μt,i=p(st=i),因为 T i , j = p ( s t + 1 = i ∣ s t = j ) T_{i,j}=p(s_{t+1}=i|s_t=j) Ti,j=p(st+1=i∣st=j),所以 μ t + 1 = T μ t \mu_t+1=T\mu_t μt+1=Tμt
markov decision process
M
=
{
S
,
A
,
T
,
r
}
M = \{S,A, T, r\}
M={S,A,T,r}
其中:
3.
S
S
S是state
4.
T
T
T是transition operator
5.
A
A
A是action space,在上面的基础上加上action,有
T
i
,
j
,
k
=
p
(
s
t
+
1
=
i
∣
s
t
=
j
,
a
t
=
k
)
T_{i,j,k}=p(s_{t+1}=i|s_t=j,a_t=k)
Ti,j,k=p(st+1=i∣st=j,at=k)
6.
r
:
S
×
A
→
R
r: S \times A \rightarrow \mathbb{R}
r:S×A→R
partially observed markov decision process
和markov decision process相似,但是有一个observation限制,即:
M
=
{
S
,
A
,
O
,
T
,
E
,
r
}
M = \{S,A, O, T, E, r\}
M={S,A,O,T,E,r}
其中:
7.
S
S
S是state
8.
T
T
T是transition operator
9.
A
A
A是action space,在上面的基础上加上action,有
T
i
,
j
,
k
=
p
(
s
t
+
1
=
i
∣
s
t
=
j
,
a
t
=
k
)
T_{i,j,k}=p(s_{t+1}=i|s_t=j,a_t=k)
Ti,j,k=p(st+1=i∣st=j,at=k)
10.
r
:
S
×
A
→
R
r: S \times A \rightarrow \mathbb{R}
r:S×A→R
11.
E
E
E是emission prob,即
p
(
o
t
∣
s
t
)
p(o_t|s_t)
p(ot∣st)
RL’s goal
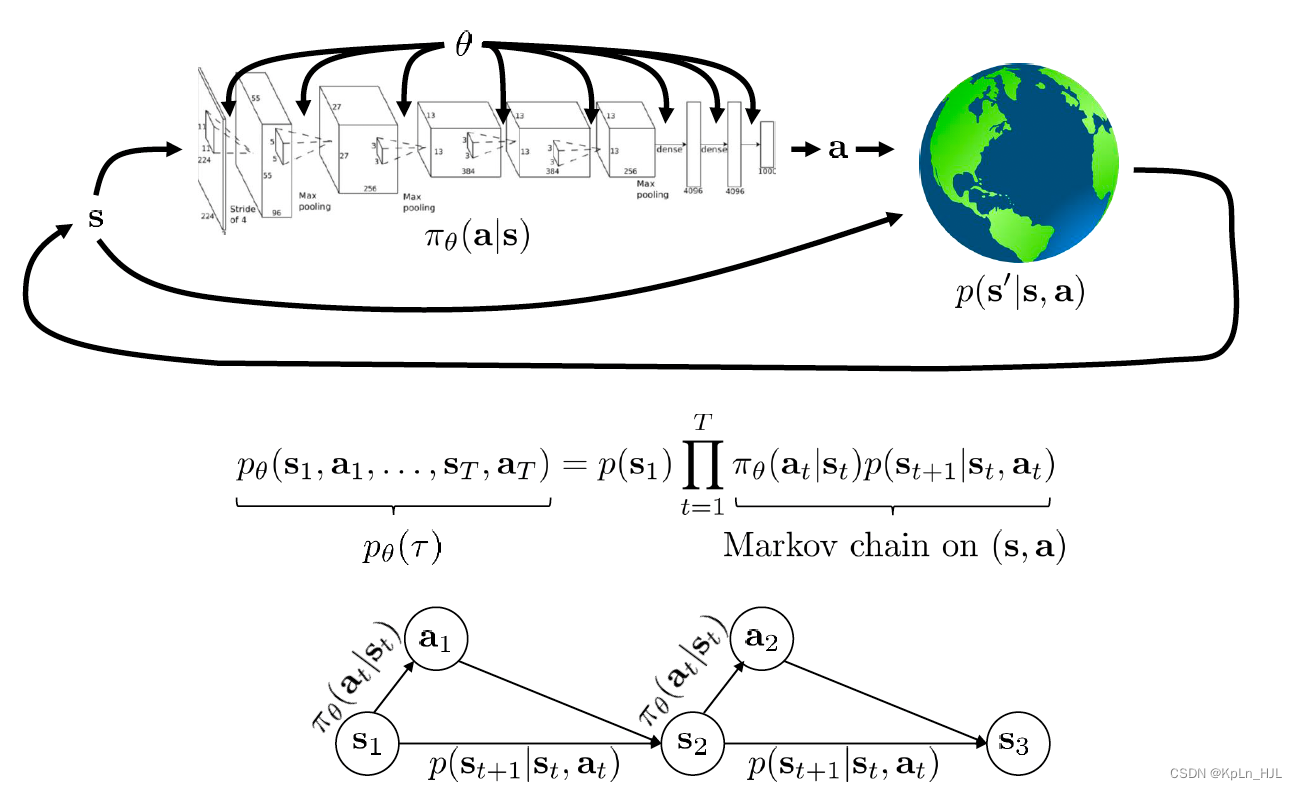
强化学习的goal function如下:
θ
∗
=
arg max
θ
E
τ
∼
p
θ
(
τ
)
[
∑
t
r
(
s
t
,
a
t
)
]
\theta^*=\argmax_{\theta}E_{\tau \sim p_\theta(\tau)}[\sum_t r(s_t, a_t)]
θ∗=θargmaxEτ∼pθ(τ)[t∑r(st,at)]
transitions follow markov process
Q & A
RL和MDP/markov decision process是什么关系?
RL是一个解决MDP问题的框架
如果一个问题可以被定义为MDP问题(能够给出transition prob和reward distribution),那么RL可能比较适合来解决这个问题。反过来,如果问题不能被定义为MDP,那么RL可能不能保证能找到useful solution
影响RL的一个关键因素是states是否具有markov property(一个随机过程在给定现在状态和过去所有状态的情况下,其未来状态的条件概率分布仅依赖于当前状态)