队列
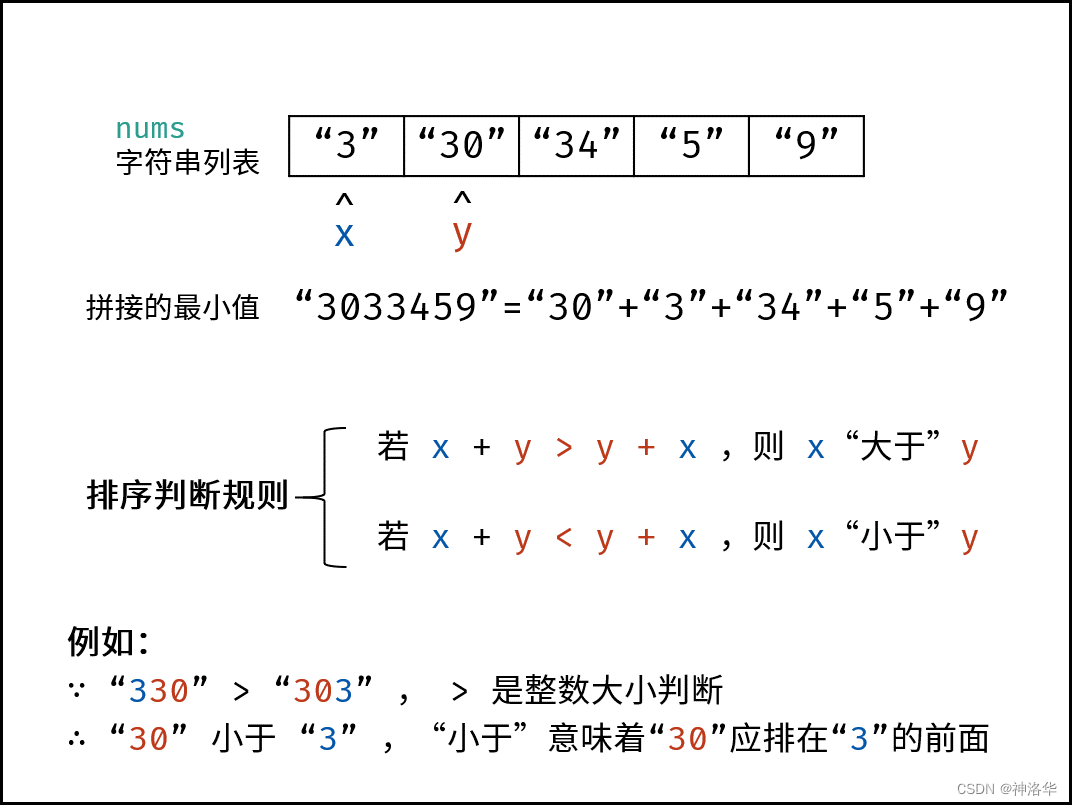
- 队列(Queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除。
进行插入的一端称为队尾(rear),插入动作称为进队或入队
进行删除的一端称为队头(front),删除动作称为出队
队列的性质:先进先出(First-in, First-out)
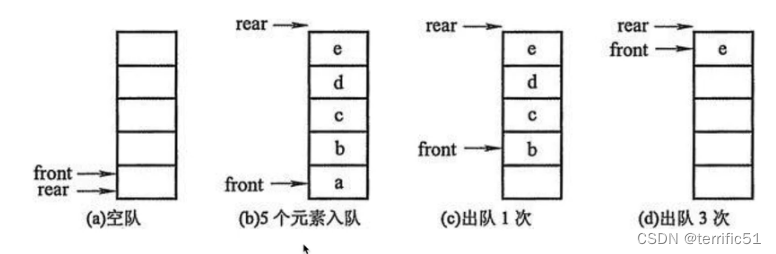
队列前出后进
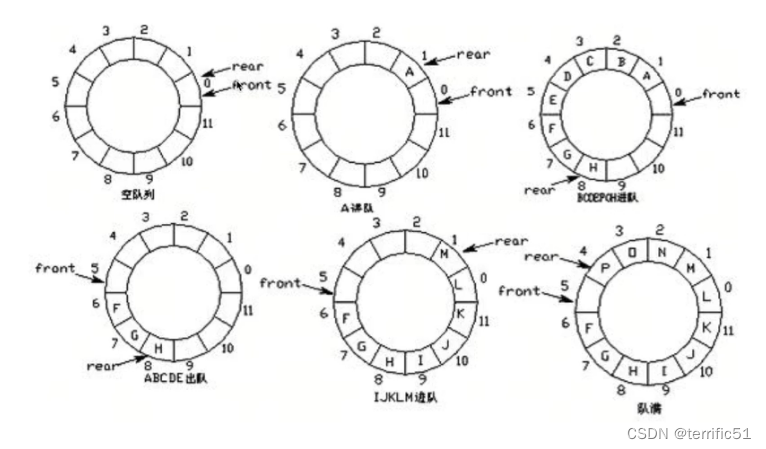
- 环形队列:
当队尾指针front等于Maxsize + 1时,再前进一个位置就自动到0.
1队首指针前进1: front = (front + 1) % MaxSize
2队尾指针前进1: rear= (rear + 1) % MaxSize
3队空条件: rear等于front
4队满条件: (rear + 1) % MaxSize==front - 测试
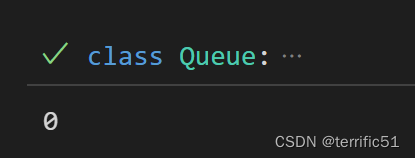
class Queue:
def __init__(self,size=100) :
self.queue=[0 for _ in range(size)]
self.size=size
self.rear=0 #队尾指针
self.front=0 #队首指针
def push(self,element): #后进队
if not self.is_filled():
self.rear=(self.rear+1) % self.size
self.queue[self.rear]=element
else:
raise IndexError("Queue is filled.")
def pop(self): #前出队
if not self.is_empty():
self.front=(self.front+1) % self.size
return self.queue[self.front]
else:
raise IndexError("Queue is empty.")
#判断队空
def is_empty(self):
return self.rear==self.front
#判断队满
def is_filled(self):
return (self.rear+1) % self.size==self.front
q=Queue(5)
for i in range(4):
q.push(i)
print(q.pop())
q.push(3)
Python队列内置模块
使用方法: from collections import deque
创建队列: queue = deque()
进队: append()
出队: popleft()
双向队列队首进队: appendleft()
双向队列队尾出队: pop()
- 利用队列输出文件后五行
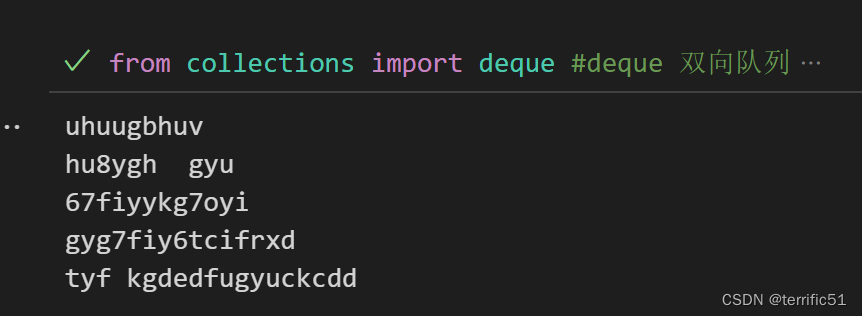
from collections import deque #deque 双向队列
def tail(n):
with open('test.txt','r')as f:
q=deque(f,n)
return q
for line in tail(5):
print(line,end='')
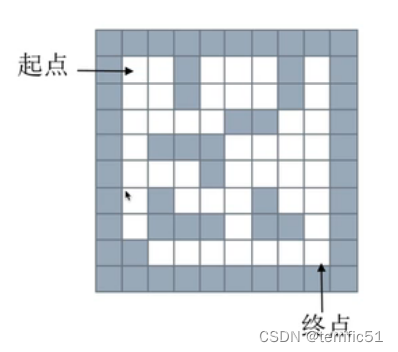
迷宫问题
给一个二维列表,表示迷宫(0表示通道,1表示围墙)。给出算法,求一条走出迷宫的路径。

- 栈——深度优先搜索
回溯法
思路:从一个节点开始,任意找下一个能走的点,当找不到能走的点时,退回
上一个点寻找是否有其他方向的点。使用栈存储当前路径
#栈
maze =[
[1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
#x,y四个方向 x-1,y;x+1,y;x,y-1;x,y+1
dirs=[
lambda x,y:(x+1,y),
lambda x,y:(x-1,y),
lambda x,y:(x,y-1),
lambda x,y:(x,y+1)
]
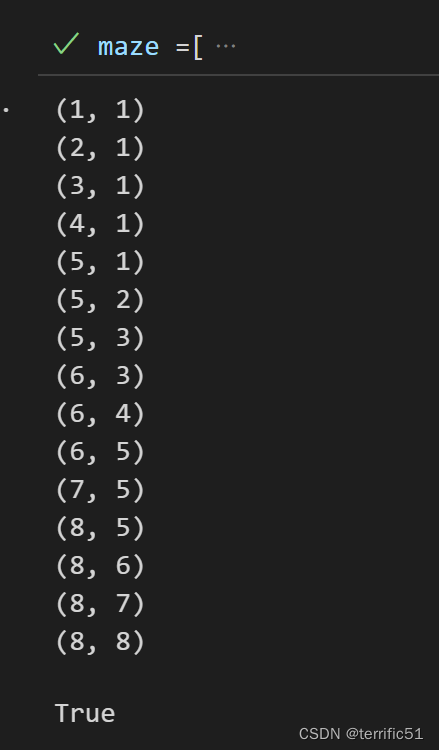
def maze_path(x1,y1,x2,y2): #起点x1,y1;终点x2,y2
stack=[]
stack.append((x1,y1))
while(len(stack)>0):
curNode=stack[-1] #当前的节点
if curNode[0]==x2 and curNode[1]==y2:
#走到终点
for p in stack:
print(p)
return True
for dir in dirs:
nextNode=dir(curNode[0],curNode[1])
#如果下一个节点能走
if maze[nextNode[0]][nextNode[1]]==0:
stack.append(nextNode)
maze[nextNode[0]][nextNode[1]]=2 #2表示为已经走过
break
else:
maze[nextNode[0]][nextNode[1]]=2
stack.pop()
else:
print("没有路")
return False
maze_path(1,1,8,8)
- 队列——广度优先搜索
思路:从一个节点开始,寻找所有接下来能继续走的点,继续不断寻找,直到找到出口。
使用队列存储当前正在考虑的节点






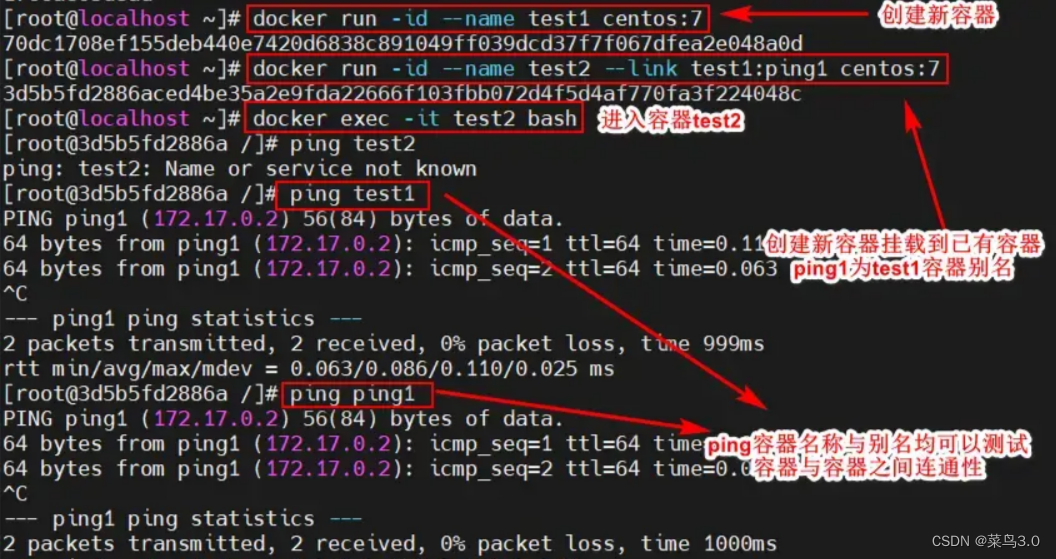
![[golang] 实现 jwt 方式登录](https://img-blog.csdnimg.cn/e439f519f6ce4d8dbff25abd86eefffc.png)