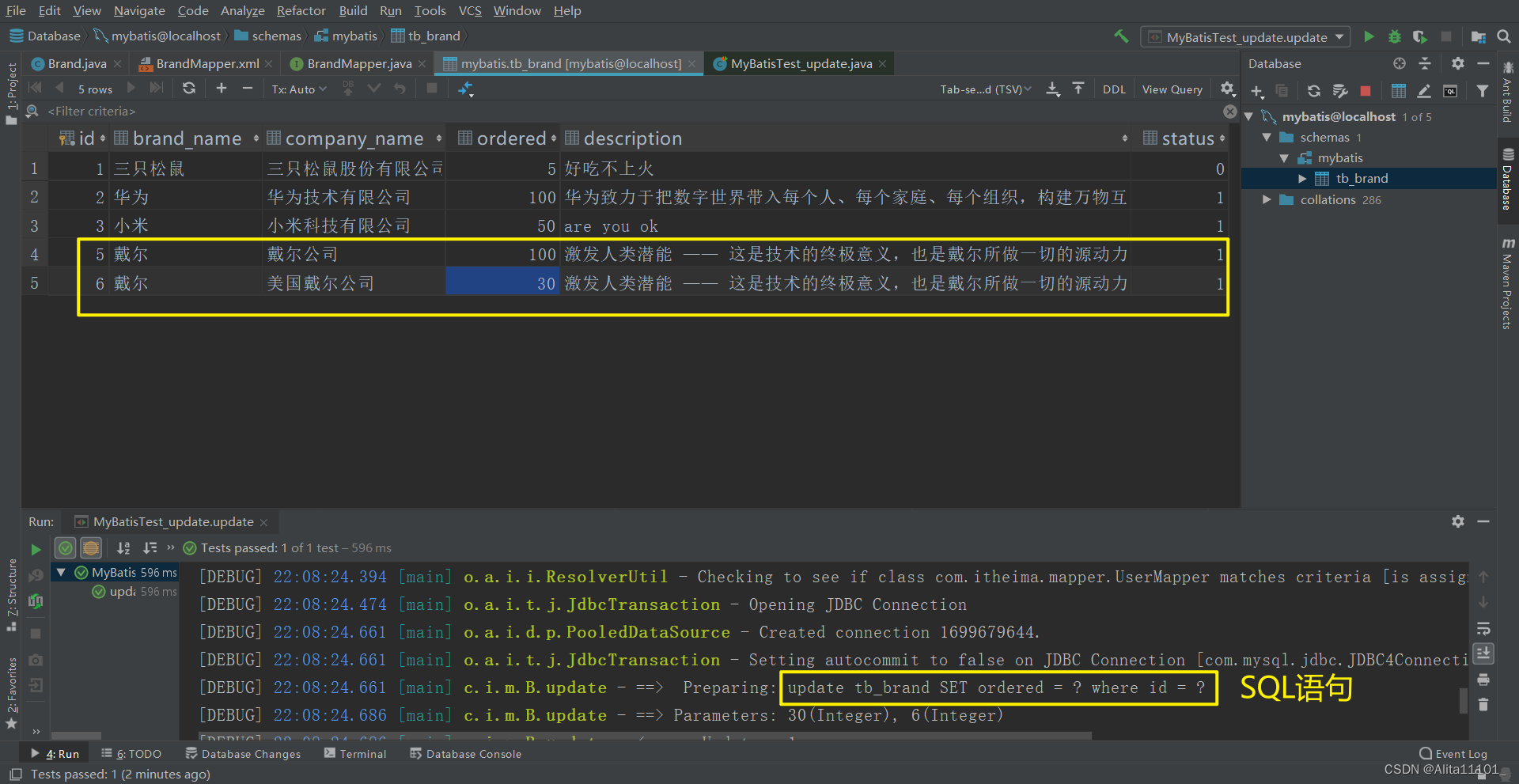
题目描述
小张冒充 X 星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n×n 个方格。如下图所示。
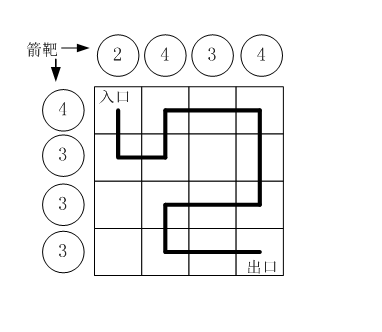
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入描述
第一行一个整数 N (0≤N≤20),表示地面有 N×N 个方格。
第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出描述
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3 ⋯⋯
比如,上图中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
输入输出样例
示例
输入
4
2 4 3 4
4 3 3 3
输出
0 4 5 1 2 3 7 11 10 9 13 14 15思路:
DFS:题目要求输出一条路径,用DFS很合适,DFS搜索过程中,自然生成一条路径。
剪枝:每走到一个格子,对应的靶子上箭多一支,靶子上的箭等于给定的数字后,就不用再DFS下去了。(或者做减法,靶子的数字减到0)
记录路径的技巧:根据题目的要求,用栈来跟踪DFS的过程,记录DFS走过的路径,是最方便的。DFS到某个格子时,把这个格子放到栈里,表示路径增加了这个格子。DFS回溯的时候,退出了这个格子,表示路径上不再包括这个格子,需要从栈中弹走这个格子。
参考代码:
def dfs(x,y):
if a[x]<0 or b[y]<0:#先开头检验是否符合标准
return
if x==n-1 and y==n-1:#走到终点
flag=1
for i in range(n): #检查每个箭靶上的数字是否减尽
if a[i]!=0 or b[i]!=0:
flag=0
return
if flag==1:
for i in range(len(path)):
print(path[i],end=' ')
l=[(1,0),(-1,0),(0,-1),(0,1)]
for i in range(4):
xt=x+l[i][0]
yt=y+l[i][1]
if 0<=xt<n and 0<=yt<n and vis[xt][yt]==0:
vis[xt][yt]=1 #标记现场
path.append(xt*n+yt) #这个是坐标的计算方法
a[xt]-=1; b[yt]-=1
dfs(xt,yt)
path.pop()
a[xt]+=1; b[yt]+=1 #还原现场
vis[xt][yt]=0
n=int(input())
vis=[[0]*n for i in range(n)]
path=[]
path.append(0)
b=list(map(int,input().split()))
a=list(map(int,input().split()))
vis[0][0]=1
a[0]-=1; b[0]-=1
dfs(0,0)