题目大意：

N 头牛 ， 每头牛有一个重量(Weight)和一个力量(Strenth) ， N头牛进行排列 ， 第 i 头牛的风险值为其上所有牛总重减去自身力量 ， 问如何排列可以使最大风险值最小 ， 求出这个最小的最大风险值；

思路：临项交换

邻项交换排序是一种常见的贪心算法，通过比较两个相邻元素交换前后的优劣对整个序列进行排序，从而使得这个序列成为题目所求的最优解。

我们假设前 i 项已经是最优排列 ， 且第 i + 1 项和第 i + 2 项当前排列时最优

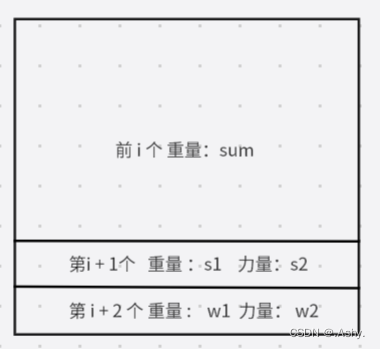
那么对于第 i + 1 个
$re{s}_{i+1}=sum-s_2$
对于第 i + 2 个
$re{s}_{i+2}=sum+s_1-w_2$

若我们交换第 i + 1 项 和 第 i + 2 项

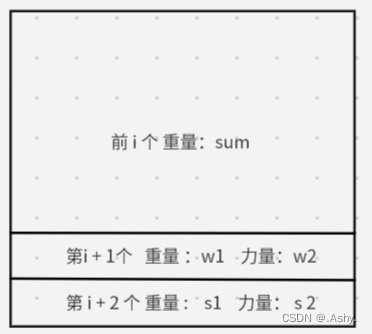
那么对于第 i + 1 个
$re{s}_{i+1}^{\prime }=sum-w_2$
对于第 i + 2 个
$re{s}_{i+2}^{\prime }=sum+w_1-s_2$

在这里我们已经假设交换前为最优状态 ， 所以我们根据题目中最大值最小的定义可以得到下面这个式子
$max(re{s}_{i+1},re{s}_{i+2})<=max(re{s}_{i+1}^{\prime },re{s}_{i+2}^{\prime })$
转化一下
$max(sum-s_2,sum+s_1-w_2)<=max(sum-w_2,sum+w_1-s_2)$
每一项 减去 sum 加上 ($s_2+w_2$)
$max(w_2,s_1+s_2)<=max(s_2,w_1+w_2)$
至此 ， 我们就推出了我们想要的交换方程

bool cmp(node a,node b){
	return max(a.x + a.y , b.y) < max(b.x + b.y , a.y) || (max(a.x + a.y , b.y) == max(b.x + b.y , a.y) && a.x + a.y < b.x + b.y); 
}

这里等于号要特判 ，不懂的可以看看下面这个博客
浅谈邻项交换排序的应用以及需要注意的问题

当我们排好序后 ，不要忘记我们的问题 ， 是要求最小的最大值 ，这是只要遍历所有状态求出最大值即可。

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
typedef long long ll;
const int N = 2e5+10;
const int p = 1e9 + 7;
typedef pair<int,int>PII;
const int inf = 1 << 31 - 1;
const double eps = 1e-9;

int n;

struct node{
	int x,y;
}a[N];

bool cmp(node a,node b){
	return max(a.x + a.y , b.y) < max(b.x + b.y , a.y) || (max(a.x + a.y , b.y) == max(b.x + b.y , a.y) && a.x + a.y < b.x + b.y); 
}

int main(){

	IOS
	
	cin >> n;
	for(int i=1;i<=n;i++){
		cin >> a[i].x >> a[i].y;
	}
	
	sort(a+1,a+1+n,cmp);

	int ans = -inf , sum = 0;
	
	for(int i=1;i<=n;i++){
		sum += a[i-1].x;
		ans = max(ans , sum - a[i].y);
	}
	
	cout << ans ;

	
	return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);