1.什么是哈夫曼树?
哈夫曼树经典问题:
合并果堆问题:
如果有三个果堆,其质量分别是1,2,3,我们现在需要将这三堆合并成一堆果堆,合并过程消耗体力等于两堆果堆的质量之和,求最小体力消耗值?
答:首先,不要以为无论怎么搭配消耗的体力是一样的
如果先13,得到一个4的果堆,消耗体力为4,再和2合并,42,得到一个6的果堆,消耗体力为6,总共消耗体力为(4+6) = 10。
如果是先12,则得到一个3的果堆,消耗体力为3,再和3合并,33,得到一个6的果堆,消耗体力为6,总共消耗体力为(3+6) = 9。
2+3 = 5, 5 + 1 = 6, (5+6) = 11。
综上所述, 2情况下的体力消耗值最小。
哈夫曼树就是为了解决该类问题而提出的
如何用哈夫曼树解决以上的问题?
让果堆作为叶子结点,权值为果堆的重量,那么非叶子结点就是合并出来的果堆的质量,也可以说是合并这次消耗的体力值,那么从根结点到叶子结点的和就是总共消耗的体力值,这样遍历所有到叶子结点的路径(非叶子结点之和)即可找出最小消耗体力值。
这样就可以画出三棵哈夫曼树:
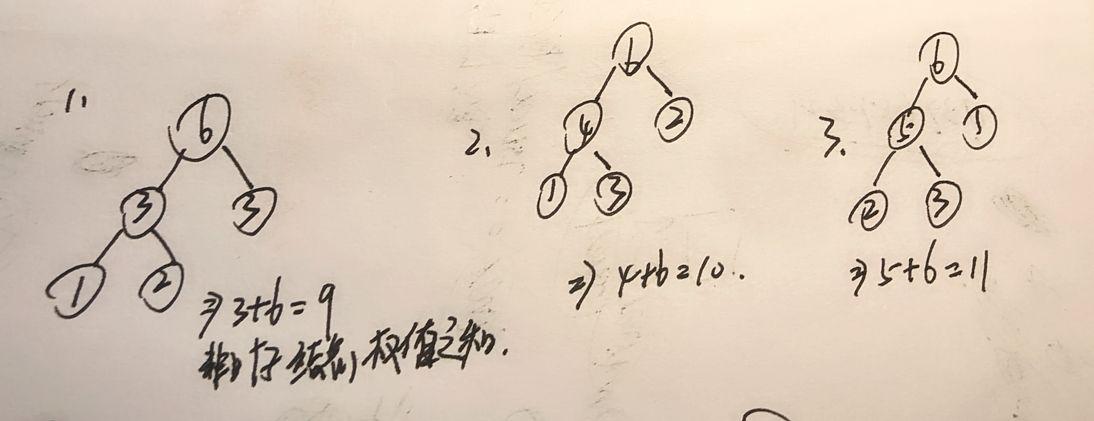
由此可以看出一个问题的哈夫曼树不只有一颗,一颗哈夫曼树有唯一解,但这颗不一定是这个问题的最优解。
事实上,该哈夫曼树的解也可以通过求树的带权路径长度(weighted path length of tree)(WPL),带权路径长度就是步长*该结点的权值,它等于所有叶子结点的带权路径长度之和,步长即从根结点出发到达该结点所经过边数。
如1,就是(1*2)+(2*2)+(1*3) = 9,为所求。

//由上面三张图可知,哈夫曼树不唯一,但是最小带权路径长度唯一。
因此:
哈夫曼树就是最优二叉树,哈夫曼树用于求最小带权路径长度。(求多种配合方案的唯一最有解)
2.如何建立一颗哈夫曼树?

n个结点,每个结点看作一棵树
当前根结点权值最小的两棵树两两合并//有点像贪心
重复2,直到只剩一棵树,这个树就是哈夫曼树。

以果堆问题为例:
使用优先队列(小顶堆)(priority_queue),每次从优先队列拿出两个最小权值,相加后再入队,重复直到只剩一个权值时结束,相加的时候再设置一个外部变量ans将相加结果记录,最后ans的值即为树的最小路径长度。
(相加结果的反复相加之和)
优先队列:队首元素一定是当前队列中优先级最高的那个一个。(默认从大到小)
如何用优先队列定义一个小顶堆:
priority_queue<long long, vector<long long>, greater<long long>>q
//第一个是优先队列存储元素类型,第二个是实现堆使用的容器,第三个是优先级设置。

3.什么是哈夫曼编码?

为了方便数据传输,将字符串转换成01串的形式,设A:0 B:1 C:00 D:01
那么ABCAD就为0100001,我们发现前缀“01”既可能是AB也可能是D,产生了二意性,A的编码是D的前缀,那么有其他字符和A拼接就有可能产生D,因此这种做法是错误的。


原理就是利用哈夫曼编码,因为叶子结点的编码代表到叶子结点的路径,是唯一的。


//结点的前缀编码的长度等于步长,步长*权值 = 带权路径长度,因此字符串编码成01串后的长度实际上就是这棵树的带权路径长度。

//哈夫曼树的出现,可以使得前缀编码的长度最短,这个最短的前缀编码叫做哈夫曼编码。
(即如何根据字符出现的次数(质量)来设置一颗哈夫曼树,让其树的带权路径长度最小(体总力消耗))。