题目描述

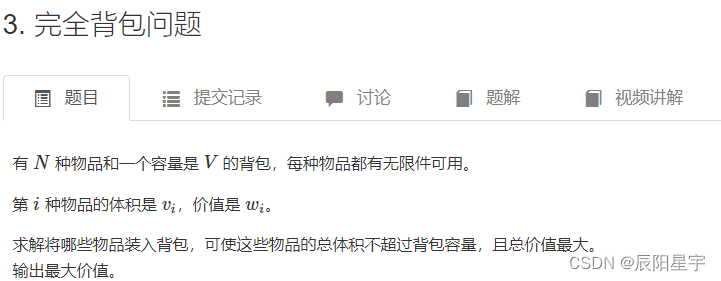
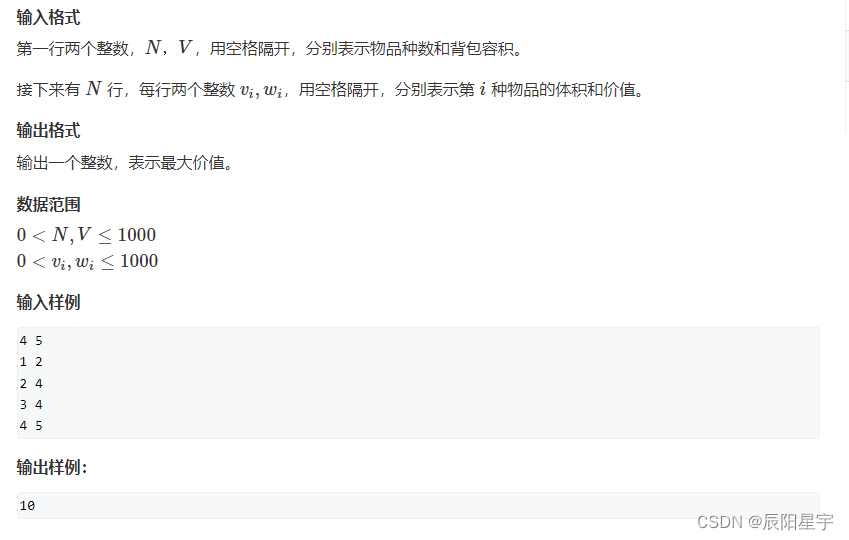
原题链接：3. 完全背包问题

解题思路

完全背包相对于01背包来说，对同一个物品可以选择多次。而01背包对同一个物品只能选择一次。

递推公式上的区别：01背包是dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])，完全背包是dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])。

（1）dp[i][j]二维数组

• 动态规划五步曲：

（1）dp[i][j]含义： 在背包容量为j的条件下，从0-i中选取物品，可达到的最大价值。

（2）递推公式： dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])，该公式是由两个公式联立而成。
公式1：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i], dp[i - 1][j - 2*v[i]] + 2*w[i] + ... + dp[i - 1][j - n*v[i]] + n*w[i])，其中n*v[i]是刚好小于等于j。该公式是说明，在同一物品可多次选择的条件下，不选该物品和选择该物品时，取得一个最大价值的方案。
公式2：dp[i - 1][j - v[i]] + w[i]= max(dp[i - 1][j - v[i]], dp[i - 1][j - 2*v[i]] + w[i], dp[i - 1][j - n*v[i]] + (n-1)*w[i]) + w[i]，是由公式1的逻辑演化而来。

（3）dp数组初始化： dp[i][0] = 0，容量为0时，价值为0。

（4）遍历顺序： 先背包再物品，或者先物品再背包都可以，顺序是从小到大。

（5）举例： （省略）

#include <iostream>

using namespace std;

const int N = 1010;
int dp[N][N];
int v[N], w[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++)      cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = 1;j <= m; j++) {
            if(v[i] > j)        dp[i][j] = dp[i - 1][j];
            else                dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
        }
    }
    
    cout << dp[n][m] << endl;
    
    return 0;
}

（2）d[j]一维滚动数组

• 动态规划五步曲：

（1）dp[j]含义： 在背包容量为j的条件下，从0-i中选取物品，可达到的最大价值。

（2）递推公式： dp[j] = max(dp[j], dp[j - v[i]] + w[i])，按照一定的遍历顺序要与二维中的公式等价。

（3）dp数组初始化： dp[0] = 0，容量为0时，价值为0。

（4）遍历顺序： 先背包再物品，或者先物品再背包都可以，顺序是从小到大，从而实现，在外层值固定时，内层for循环遍历过程中，可以加到之前已加上的数据信息。

（5）举例： （省略）

#include <iostream>

using namespace std;

const int N = 1010;
int dp[N];
int v[N], w[N];
int n, m;


int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++)      cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++) {
        for(int j = v[i]; j <= m; j++) {
            // dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])
            dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    
    cout << dp[m] << endl;
    
    return 0;
    
}