题目描述

如下图所示，3 x 3 的格子中填写了一些整数。

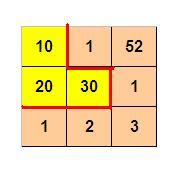
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是 60。

本题的要求就是请你编程判定：对给定的 m×n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。

如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。

如果无法分割，则输出 0。

输入描述

输入描述

程序先读入两个整数 m,n 用空格分割 (m,n<10)，表示表格的宽度和高度。

接下来是 n 行，每行 m 个正整数，用空格分开。每个整数不大于 10^4。

输出描述

在所有解中，包含左上角的分割区可能包含的最小的格子数目。

输入输出样例

示例

输入

3 3
10 1 52
20 30 1
1 2 3

输出

3

 思路：

先求所有格子的和sum，再用DFS 找一个联通区域，看这个区域的和，是否为：sum/2

结束的条件：

        1、分割格子的数字和的2倍等于总和

        2、格子超出范围

        3、数字和超出范围（大于总和的一半）

参考代码：

def dfs(x,y,c,s):  # c 表示当前分割的格子，s 表示数字和
  global ans,sum_num
  if 2*s>sum_num:
    return
  if 2*s==sum_num:
    if ans>c and vis[0][0]==1: #若当前分割格子小于前一个分割的格子且包含第一个格子
      ans=c            #将格子更新
    return
  vis[x][y]=1  #标记使用
  l=[(1,0),(-1,0),(0,1),(0,-1)] #上下左右四个方向
  for i in range(4):
    xt=x+l[i][0]
    yt=y+l[i][1]
    if 0<=xt<n and 0<=yt<m:  #未超出范围才可以dfs
      if vis[xt][yt]==0:
        dfs(xt,yt,c+1,s+a[x][y])
  vis[x][y]=0
a=[]
m,n=map(int,input().split())  #读入数据，n 行 ，m 列
for i in range(n):       #读入格子数据
  b=list(map(int,input().split()))
  a.append(b)
sum_num=0  #计算总和
vis=[[0]*m for _ in range(n)]
for i in a:
  sum_num+=sum(i)
ans=100000
dfs(0,0,0,0)
print(ans)

---

剪枝 ：

        可行性剪枝：对当前状态进行检查，如果当前条件不合法就不再继续，直接返回。
        搜索顺序剪枝：搜索树有多个层次和分支，不同的搜索顺序会产生不同的搜索树形态。
        最优性剪枝：在最优化问题的搜索过程中，如果当前花费的代价已超过前面搜索到的最优解，那么本次搜索已经没有继续进行下去的意义，停止对当前分支的搜索。
        排除等效冗余：搜索的不同分支，最后的结果是一样的，那么只搜一个分支就够了。
        记忆化搜索：在递归的过程中，有许多分支被反复计算，会大大降低算法的执行效率。将已经计算出来的结果保存起来，以后需要用到的时候直接取出结果，避免重复运算，从而提高了算法的效率。