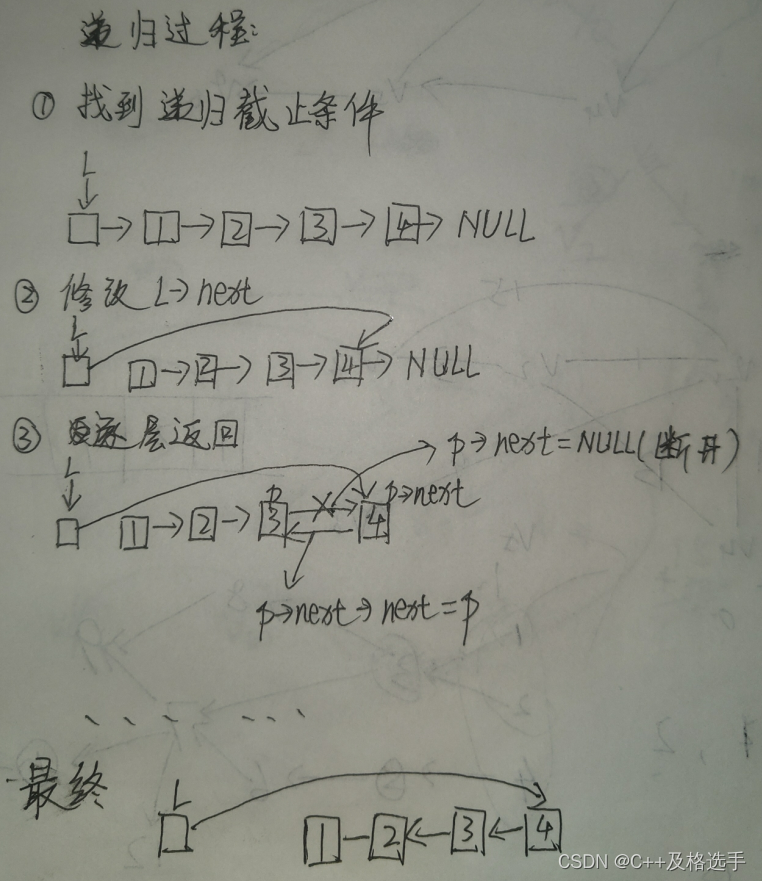
本节内容只有通过例题来记录效果才是最好的,请看下面内容！

递归实现二分法

经典二分查找问题：LintCode 炼码

描述**：**在一个排序数组中找一个数，返回该数出现的任意位置，如果不存在，返回 -1。 输入：nums = [1,2,2,4,5,5], target = 2 输出：1 或者 2

     def findPosition(self, nums, target):
        def binarysearch(nums,start,end,target):
            middle = (start+end)//2

            # if((start==end and nums[start]!=target) or start>end):
                # return -1

            if(start>end): #这里是>还是>= ？ 留给自己思考！
                return -1

            if(nums[middle]==target):
                return middle
            if(nums[middle]<target):
                return binarysearch(nums, middle+1, end, target)
            else:
                return binarysearch(nums, start, middle-1, target)

        # write your code here
        if(nums==[] or nums == None):
            return -1

        return binarysearch(nums, 0, len(nums)-1, target)

非递归实现二分法

请注意，非递归二分法非常常用，尤其在双指针里面。但是这类题目的一个难点就是搞不拎清到底是'>='('<=')还是'>'('<')，到底是 left = middle + 1 （right = middle - 1）还是 left = middle （right = middle）。那么，本章节将会彻底讲明白这些坑，并给出一个万能二分模板解决一系列问题。在进行下面的例题讲解时，先搞清楚这几种循环结束时条件的值(假设都是 +=1)：while(left<right)、while(left<=right)、while(left+1<right)，第一种结束时 left==right ,第二种是left = right + 1，第三种是 left ==right - 1；

经典二分查找问题：LintCode 炼码

描述**：**在一个排序数组中找一个数，返回该数出现的任意位置，如果不存在，返回 -1。 输入：nums = [1,2,2,4,5,5], target = 2 输出：1 或者 2 使用经典非递归算法实现：

def findPosition(nums, target): 
    # write your code here
    if(nums==[] or nums == None):
        return -1

    left = 0
    right = len(nums)-1

    while(left<=right): # 这里是'<='还是 '<' ?
        middle = (left+right)//2
        if(nums[middle]==target):
            return middle
        if(nums[middle]<target):
            left = middle+1
            if(nums[middle]>target):
                right = middle-1
    #if(nums[left]==target):
    #    return left;
    return -1

解释：那么上述代码中第9行到底要不要加上'='呢？答案是既可以使用"<="，也可以使用"<"；这里举例说明，假设nums = [3] 只有一个元素，那么left = 0 ，right = 0 。如果加上"="号那么，这种情况依旧可以进入while中进行判断，也就是说while循环已经conver到了这种情况，所以可以加上。如果不加"="，那么需要单独判断这种特例，那就需要17，18行的代码。总结就是，当遇到这种情况搞不清楚时，举一个只有一个元素数组的特例，看看是否当用"<="时 while 循环能否cover到取等于的情况，如果能就加上等号，如果不能就针对特例另外写判断。一般建议写不加等于号的情况，将等于的情况单独拿出来判断，这样可以避免很多边界值问题。好的，接下来是难度大一点的二分查找，这里特别注意边界条件！不然，很容易错，可以先自己做做再看解析： 目标最后位置:LintCode 炼码 **描述:**给一个升序数组，找到 target 最后一次出现的位置，如果没出现过返回 -1 输入：nums = [1,2,2,4,5,5], target = 2 输出：2

    def last_position(self, nums: List[int], target: int) -> int:
        # write your code here

        if(nums==None or nums==[]):
            return -1

        left=0;right=len(nums)-1
        while(left+1<right):
            middle = (left+right)//2
            if(nums[middle]==target):
                left = middle   # 不能是middle+1，这样会跳过middle
            if(nums[middle]<target):
                left = middle+1
            if(nums[middle]>target):
                right = middle-1
        if(nums[right]==target):
            return right
        if(nums[left]==target):
            return left
        return -1

解析：这道题是要找到最后一个等于target值的数字的下标，这个时候只需要将第11行代码直接返回中间值改成让left = middle，也就是说当找到一个中间值等于target时我们并不直接返回，而是包含这个middle继续向后查找。注意，这里的判断条件必须要写出 left+1<right，不然当nums=[2,2],target=2时，则进入死循环（请自觉试试），第8行这样写的话，我们希望left = right -1时，也就是left与right相邻时结束。所以，最后第16到19行代码就必须单独判断这两个索引是否满足题意。当你会解这道题时，你应该会解下一道题： fisrt_position二分查找：LintCode 炼码 **描述：**给定一个排序的整数数组（升序）和一个要查找的整数 target，用O(logn)O(logn)的时间查找到target第一次出现的下标（从0开始），如果target不存在于数组中，返回-1。
解析：你只需要更改第11、16到19行代码即可完成！

最后给出一个二分查找题目的通用模板：

    def last_position(self, nums: List[int], target: int) -> int:
        # write your code here

        if(nums==None or nums==[]):
            return -1

        left=0;right=len(nums)-1
        while(left+1<right): # 保证循环一定会退出
            middle = (left+right)//2
            if(nums[middle]==target):
                left = middle   # 根据题意修改这里
            if(nums[middle]<target):
                left = middle  #不 +1 ，不影响结果 ，有时候+1反而错误
            if(nums[middle]>target):
                right = middle #不 -1 ，不影响结果 ，有时候-1反而错误

        # 因为循环提前一步退出了，所以最后一步自己判断
        if(nums[right]==target):
            return right
        if(nums[left]==target):
            return left
        return -1

使用通用目标解决以下问题： 排序数组中最接近元素：LintCode 炼码 **描述：**在一个排好序的数组 A 中找到 i 使得 A[i] 最接近 _target _如果数组中没有元素，则返回-1。

585· 山脉序列中的最大值：LintCode 炼码 **描述：**给 n 个整数的山脉数组，即先增后减的序列，找到山顶（最大值）。

from typing import (
    List,
)
class Solution:
    """
    @param nums: a mountain sequence which increase firstly and then decrease
    @return: then mountain top
    """
    def mountain_sequence(self, nums: List[int]) -> int:
        # write your code here
        if(nums==[] or nums==None):
            return []

        left = 0
        right = len(nums)-1
        while(left+1<right):
            middle = (left+right)//2
            if(nums[middle]>nums[middle+1]):
                right = middle
            else:
                left = middle
        return max(nums[left],nums[right])

62 · 搜索旋转排序数组：LintCode 炼码

    def search(self, a: List[int], target: int) -> int:
        # write your code here
        if(a==[] or a == None):
            return -1
        # 有一半的数一定是单调递增的，在单调的那边找就行
        left=0
        right=len(a)-1
        while(left+1<right):
            middle = (left+right)//2
            if(a[middle]>=a[left]):
                if(target>=a[left] and target<=a[middle]):
                    right = middle 
                else:
                    left = middle 

            if(a[middle]<a[right]):
                if(target>=a[middle] and target<=a[right]):
                    left = middle
                else:
                    right = middle

        if(a[left]==target):
            return left
        elif(a[right]==target):
            return right
        else:
            return -1

未排序的序列上的二分法

75 · 寻找峰值:LintCode 炼码 **描述：**给定一个整数数组(size为n)，其具有以下特点：

• 相邻位置的数字是不同的
• A[0] < A[1] 并且 A[n - 2] > A[n - 1]

假定_P_是峰值的位置则满足A[P] > A[P-1]且A[P] > A[P+1]，返回数组中任意一个峰值的位置。 输入：A = [1, 2, 1, 3, 4, 5, 7, 6] 输出：1

    def find_peak(self, a: List[int]) -> int:
        # write your code here
        if(a==[]):
            return -1
        left = 0 
        right = len(a)-1

        while(left+1<right):
            middle =(left+right)//2
            if(a[middle]>a[middle-1]):
                left = middle
            else:
                right = middle
        if(a[left]>a[right]):
            return left
        else:
            return right

在答案集合上进行二分

第一步：确定答案范围，第二步：验证答案大小 183 · 木材加工：LintCode 炼码 **描述：**有一些原木，现在想把这些木头切割成一些长度相同的小段木头，需要得到的小段的数目至少为 k。给定L和k，你需要计算能够得到的小段木头的最大长度。 输入: L = [232, 124, 456] k = 7 输出: 114 说明: 我们可以把它分成 114 的 7 段，而 115 不可以 ，对于 124 这根原木来说多余的部分没用可以舍弃，不需要完整利用

def wood_cut(self, l: List[int], k: int) -> int:
        # write your code here
        if(l==[]):
            return 0

        def cut(l,length):
            count = 0
            for i in l:
                count +=(i//length)
            return count

        start = 1
        end = sum(l)//k

        if(end<1):
            return 0

        while(start+1<end):
            middle = (start+end)//2
            if(cut(l,middle)>=k):
                start = middle
            else:
                end = middle

        if(cut(l,end)>=k):
            return end
        elif(cut(l,start)>=k):
            return start
        else:
            return -1