一、双向广搜

1、优越之处

双向广搜是指我们从终点和起点同时开始搜索，当二者到达同一个中间状态的时候，即相遇。

那么这么搜有什么好处呢？

我们知道，在很多题目中，我们使用BFS的时间复杂度是指数级别的。

也就是说，如果讲BFS的进行次数画成一个函数的话，就会画成下面这个图。

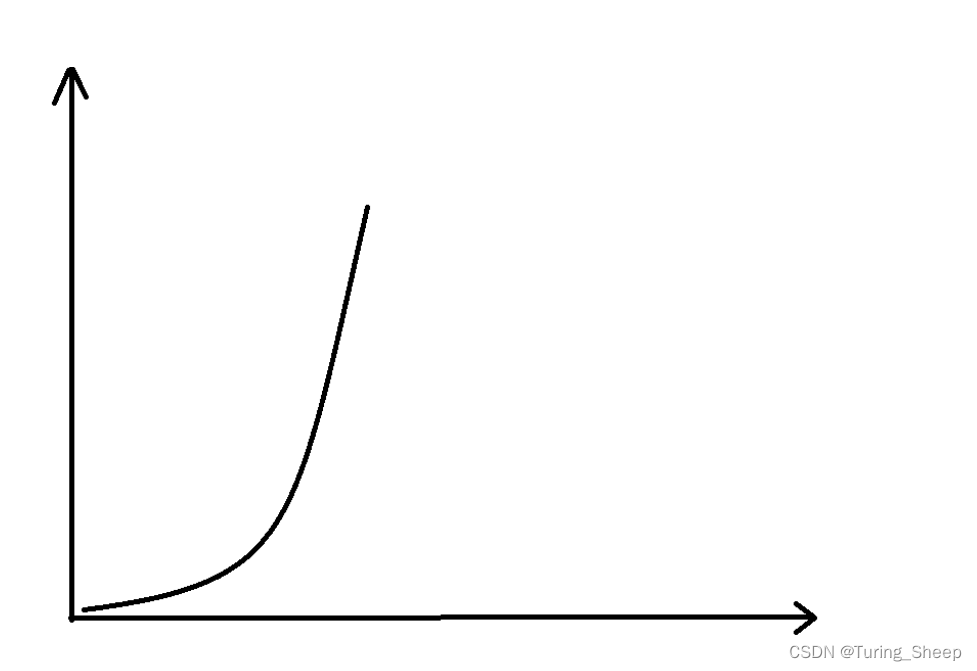
如果我们采取从两端出发，到中间某点相遇的做法。

那么示意图可以画成下面的样子：

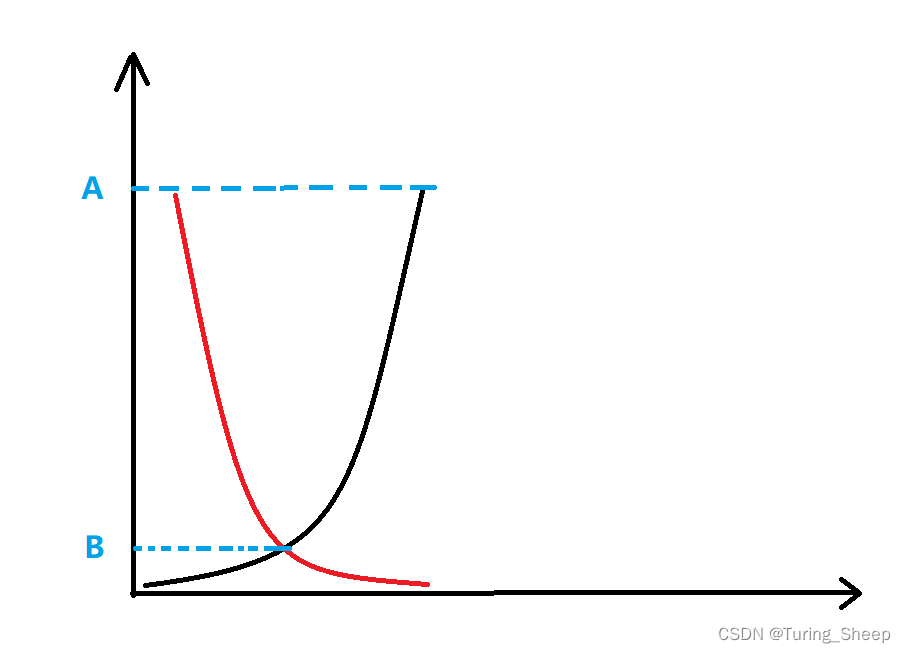
可能原来我们需要进行A次搜索，但是双向广搜的话，我们就只需要进行B次搜索。（上图仅仅表示一个大概意思，目的仅仅为了突出双向广搜进行了很大的优化，请勿追究细节）

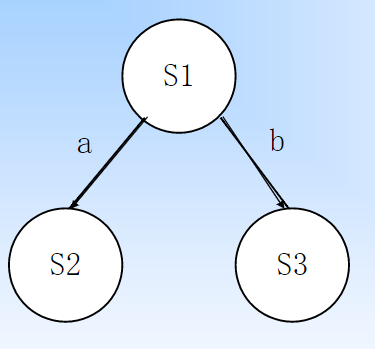
除了上面这种大致的表示方法外，我们还可以画成一个搜索树的形式来看。

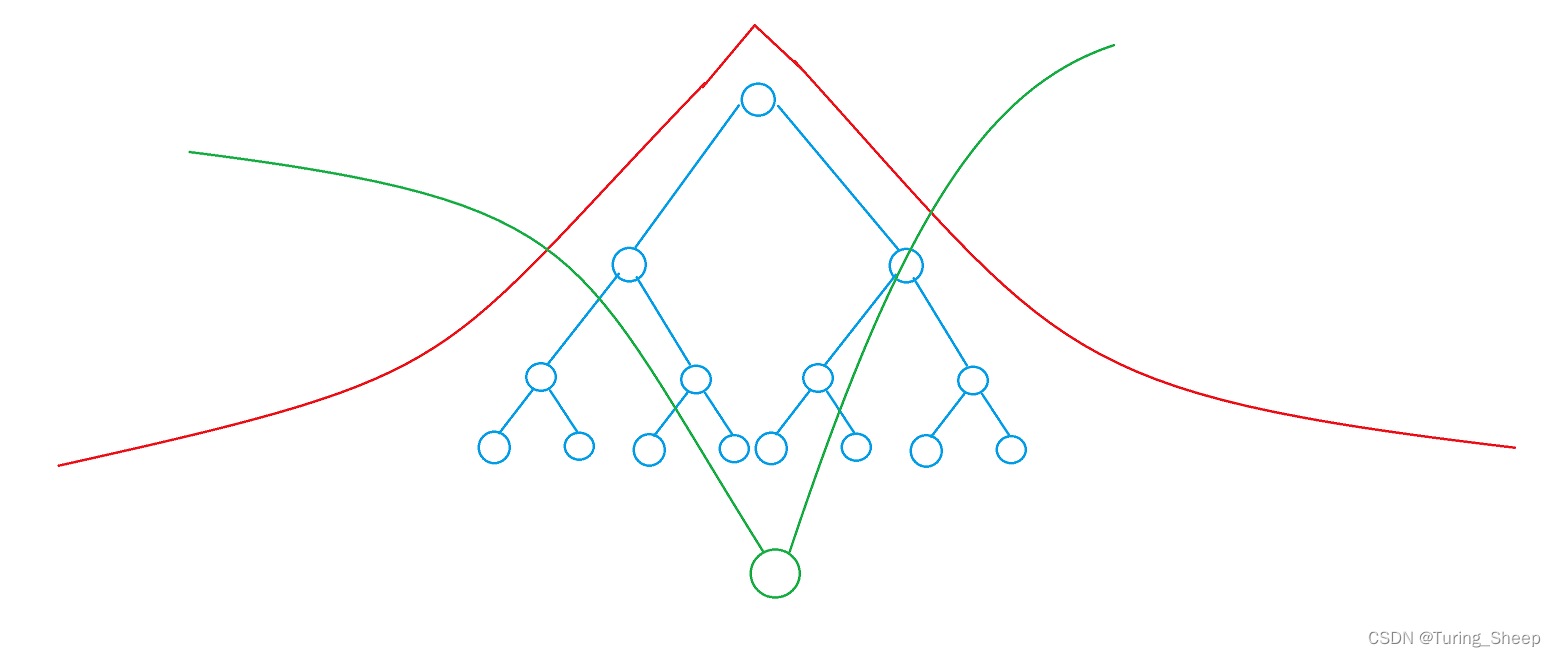
红色绿色线交叉的部分组成的菱形是双向广搜过程中所需搜索的状态数量。

上面的两个图仅仅是感性的分析了一下，双向广搜的优越之处。

我们还需要量化计算一下，到底优化了多少，具体的时间复杂度是多少，在分析复杂度之前，我们需要先看一下双向广搜大体的实现逻辑。

2、实现逻辑

我们创建两个队列。

一个队列从起点开始广搜，一个队列从终点开始广搜。

而在BFS中，我们的执行次数和队列中的元素是相关的。我们队列中的元素越多，BFS需要扩展的就越多。所以我们可以通过队列中的元素个数来代表一个BFS扩展时的复杂程度。

因此，我们可以比较两个BFS的队列中的元素，谁队列中元素少，就对哪个BFS进行拓展。

3、复杂度分析

根据上面的算法实现，我们可以知道，基本上就是从终点开始的BFS和从起点开始的BFS轮流进行。

我们可以认为二者进行的次数是一样的。

假设二者一共扩展了$K$次，那么各自可以认为进行了$k/2$次。

这里的拓展是只刚才搜索树中的层。假设每次扩展是多两个状态入队，那么总共的状态就是$1+2^1+2^2....+2^{k/2-1}$，求和以后约等于$2^{k/2}$，那么两个BFS加起来就是$2^{k/2+1}$。

如果单向广搜的话，按照刚才的求和公式，对$k$层的状态求和，大概是$2^k$

那么我们就发现优化了大约$2^{k/2}$倍。

二、例题

1、问题

2、分析

过程很简单，就是从起点开始枚举每一个可能的变化，直到最后变成了B。

由于我们已经知道了终点过程，所以可以同时从B到A开始变化。一直到二者中间状态重合。

3、代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 6;
int n;
string A, B;
string a[N], b[N];
int extend(queue<string>& q, unordered_map<string, int >&da,unordered_map<string, int>&db,string a[N], string b[N])
{
	int d = da[q.front()];
	while(q.size() && da[q.front()] == d)
	{
		auto t = q.front();
		q.pop();

		for(int i = 0; i < n; i ++ )
		{
			for(int j = 0; j < t.size(); j ++ )
			{
				if(t.substr(j, a[i].size()) == a[i])
				{
					string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size());
					if(db.count(r))return da[t] + db[r] + 1;
					if(da.count(r))continue;
					da[r] = da[t] + 1;
					q.push(r);
				}
			}
		}
	}
	return 11;
}
int bfs()
{
	if(A == B)return 0;
	queue<string>qa, qb;
	unordered_map<string, int> da, db;
	qa.push(A), qb.push(B);
	da[A] = db[B] = 0;
	int step = 0;
	while(qa.size() && qb.size())
	{
		int t;
		if(qa.size() < qb.size())
		{
			t = extend(qa, da, db, a, b);
		}
		else
		{
			t = extend(qb, db, da, b, a);
		}
		if(t <= 10)return t;
		if(++step == 10)return -1;
	}
	return -1;
}


void solve()
{
	cin >> A >> B;
	while(cin >> a[n] >> b[n])n ++;
	int t = bfs();
	if(t == -1)cout << "NO ANSWER!\n";
	else cout << t << "\n";
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	solve();
}