试题算法训练 N皇后问题

提交此题评测记录
资源限制
内存限制：256.0MB C/C++时间限制：100ms Java时间限制：300ms Python时间限制：500ms
问题描述
　　在N*N的方格棋盘放置了N个皇后，使得它们不相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在与棋盘边框成45角的斜线上。你的任务是，对于给定的N，求出有多少种合法的放置方法。
输入格式
　　输入中有一个正整数N≤10，表示棋盘和皇后的数量
输出格式
　　为一个正整数，表示对应输入行的皇后的不同放置数量。
画了个图便于理解
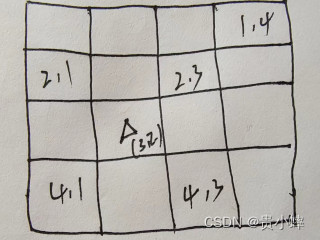
在这里插入图片描述

题目分析

图片中放置了一个皇后，可以看到右对角线他们的和相加是相等的，而左对角线他们是相减相等的。用一维数组来解决这个问题，假设存在一个皇后表示 a[i]=j;他所代表的意思是在第i行的j列放置了一个皇后。进行递归是一行一行的往下递归，约定一行只能放置一个皇后。

测试代码

#include<iostream>
#include <stdlib.h>
using namespace std;
const int N = 15;
int res = 0, n;
int a[N];
bool check(int x, int y) {
    //因为规定了a[i]=j；i表示行，j表示列，并且是一行一行往下递归
    //所以只需要看前面的行数与现在的放置冲突不
    for (int i = 1; i < x; i++) {
        //如果为同一列则不行
        if (a[i] == y)return false;
        //如果为右斜线则不行
        if (a[i] + i == x + y)return false;
        //如果为左斜线则不行
        if (i - a[i] == x - y)return false;
    }
    return true;
}
void dfs(int row) {
    //如果层数大于给定的n层数说明产生一个解
    if (row == n + 1) {
        res++;
        return;
    }
    for (int i = 1; i <= n; i++) {
        //检查是否可以放置皇后
        if (check(row, i)) {
            //可以则把第几列的值，赋给当前行
            a[row] = i;
            //去下一行寻找放置的位置
            dfs(row + 1);
            //不成功回溯回来，还原当前行的值
            a[row] = 0;
        }
    }
}
int main() {
    cin >> n;
    //从第一行开始寻找
    dfs(1);
    cout << res << endl;
    return 0;
}