(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹)
目录
定义:
两种遍历方法:
深度优先搜索(DFS):
广度优先搜索(BFS):
定义:
从已给的连通图中某一顶点出发,沿着一些边访遍图中所有的顶点,且使每个顶点仅被访
问一次,就叫做图的遍历图遍历的实质是找每个顶点的邻接点的过程
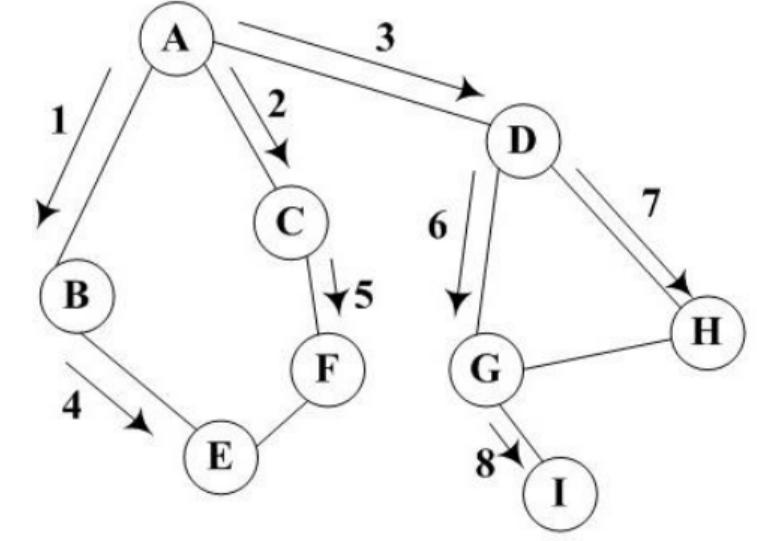
特点:图中可能存在回路 ,且图的任一顶点都可能与其它顶点相通,在访问完某个顶点之后可能会沿着某些边 又回到了曾经访问过的顶点
两种遍历方法:
深度优先搜索(DFS):
仿树的前序遍历过程 (http://t.csdn.cn/zVDgK)
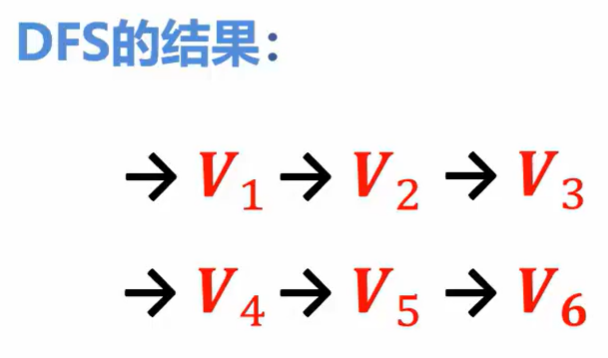
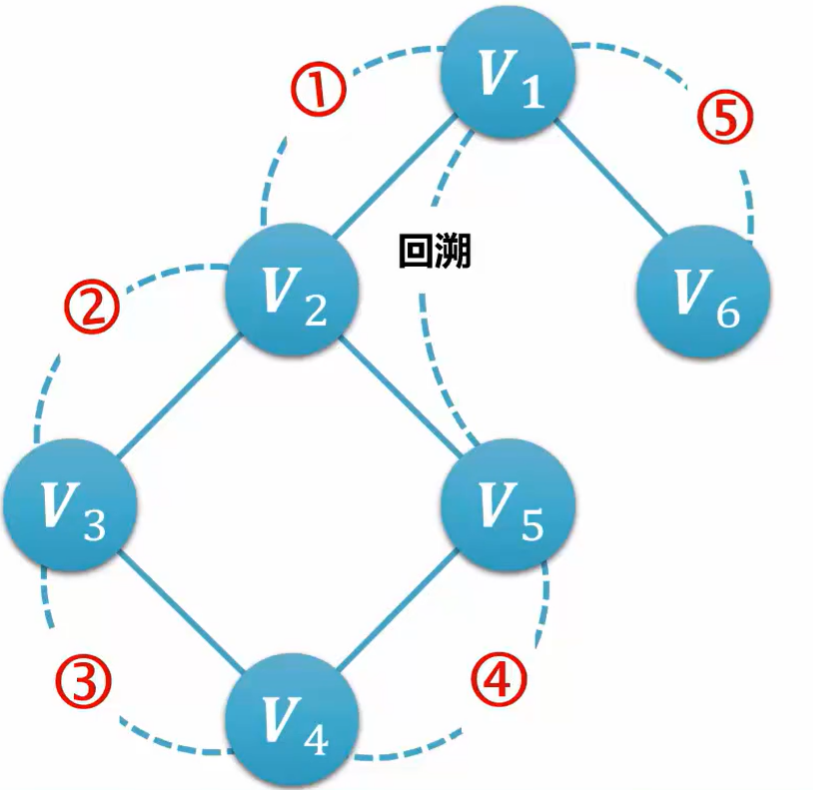
如图所示:
1.访问图中某一起始顶点V1,由V1出发,访问它的任一邻接顶点V2
2.再从V2出发,访问与V2邻接但还未被访问过的顶点V3
3.然后再从V3出发,进行类似的访问......
4.如此进行下去,直至到达所有的邻接顶点都被访问过的顶点V5为止
5,接着退回一步,退到前一次刚访问过的顶点,看是否还有其它没有被访问的邻接顶点
如果没有就再退回一步进行搜索,之后再从此顶点出发,进行与前述类似的访问,
如果有则访问此顶点
6.重复上述过程,直到连通图中所有顶点都被访问过为止
/** 保存每个顶点的访问状态[0-未访问;1-已访问 */
int visited[100];
/** 图的类型枚举 */
typedef enum
{
DG, //有向图 0
UDG, //无向图 1
DN, //有向网 2
UDN //无向网 3
}GraphKind;
/** 图的邻接矩阵存储表示 */
typedef struct
{
char* verTexs[100]; //顶点数组
int arcs[100][100]; //邻接矩阵(权数组)
int verTexCount; //图的顶点数
int arcCount; //图的边/弧数
GraphKind kind; //图的类型
}MatrixGraph;
/** 返回某个顶点在顶点集合中的下标(从0开始),不存在返回-1 */
int LocateVex(MatrixGraph* G, char* vex) {
int index = 0;
while (index < G->verTexCount) {
if (strcmp(G->verTexs[index], vex) == 0) {
break;
}
index++;
}
return index == G->verTexCount ? -1 : index;
}
/** 深度优先搜索的核心算法,index为深度搜索的某个顶点下标 */
void DFS_AMG(MatrixGraph G, int index) {
printf(" -> %s", G.verTexs[index]); //访问当前顶点
visited[index] = 1; //更改当前顶点的访问状态
for (int i = FirstAdjVex_AMG(G, G.verTexs[index]); i;
i = SecondAdjVex_AMG(G, G.verTexs[index], G.verTexs[i])) {
if (!visited[i]) {
DFS_AMG(G, i); //如果没有访问过,就继续递归调用访问
}
}
}
/** 返回顶点vex所在行中的第一个邻接点下标 */
int FirstAdjVex_AMG(MatrixGraph G, char * vex) {
int i = LocateVex(&G, vex); //找到顶点vex在顶点数组中的下标
if (i == -1) return 0;
int defaultWeight; //默认权重
defaultWeight = G.kind <= 1 ? 0 : INT_MAX; //图/网
//搜索图的邻接矩阵中与顶点vex的第一个邻接点下标
for (int j = i + 1; j < G.verTexCount; j++) {
if (G.arcs[i][j] != defaultWeight) {
return j;
}
}
return 0;
}
/** 返回与顶点vex1邻接的另一个邻接点,没有就返回0 */
int SecondAdjVex_AMG(MatrixGraph G, char * vex1, char * vex2) {
int index1 = LocateVex(&G, vex1);
int index2 = LocateVex(&G, vex2);
if (index1 == -1 || index2 == -1) return 0;
int defaultWeight;
defaultWeight = G.kind <= 1 ? 0 : INT_MAX;
for (int i = index2 + 1; i < G.verTexCount; i++) {
if (G.arcs[index1][i] != defaultWeight) {
return i;
}
}
return 0;
}
/** 邻接矩阵的深度优先遍历 */
void DFSTraverse_AMG(MatrixGraph G) {
//初始化状态数组
for (int i = 0; i < G.verTexCount; i++) {
visited[i] = 0; //初始状态设置为未访问
}
//DFS遍历
for (int i = 0; i < G.verTexCount; i++) {
if (!visited[i]) {//如果某个顶点未访问
//调用遍历函数
DFS_AMG(G, i);
}
}
}
广度优先搜索(BFS):
广度优先搜索是一种 分层 的搜索过程,每向前走一步可能访问一批顶点,不像深度优先搜索那样有回退的情况。因此,广度优先搜索 不是一个递归的过程

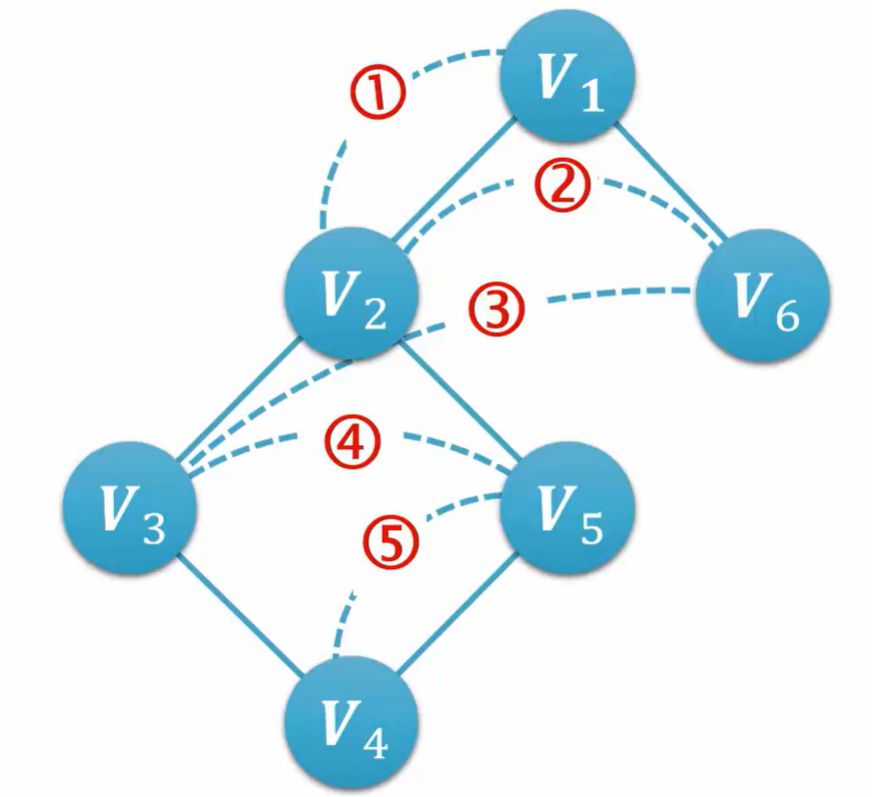
如图所示:
1.访问起始点V1
2.依次访问V1的邻接点
3.依次访问这些顶点中未被访问过的邻接点
4.直到所有顶点都被访问过为止
#include"队列.cpp"
/** 保存每个顶点的访问状态[0-未访问;1-已访问 */
int visited[100];
/** 图的类型枚举 */
typedef enum
{
DG, //有向图 0
UDG, //无向图 1
DN, //有向网 2
UDN //无向网 3
}GraphKind;
/** 图的邻接矩阵存储表示 */
typedef struct
{
char* verTexs[100]; //顶点数组
int arcs[100][100]; //邻接矩阵(权数组)
int verTexCount; //图的顶点数
int arcCount; //图的边/弧数
GraphKind kind; //图的类型
}MatrixGraph;
/** 返回某个顶点在顶点集合中的下标(从0开始),不存在返回-1 */
int LocateVex(MatrixGraph* G, char* vex) {
int index = 0;
while (index < G->verTexCount) {
if (strcmp(G->verTexs[index], vex) == 0) {
break;
}
index++;
}
return index == G->verTexCount ? -1 : index;
}
/** 返回顶点vex所在行中的第一个邻接点下标 */
int FirstAdjVex_AMG(MatrixGraph G, char* vex) {
int i = LocateVex(&G, vex); //找到顶点vex在顶点数组中的下标
if (i == -1) return 0;
int defaultWeight; //默认权重
defaultWeight = G.kind <= 1 ? 0 : INT_MAX; //图/网
//搜索图的邻接矩阵中与顶点vex的第一个邻接点下标
for (int j = i + 1; j < G.verTexCount; j++) {
if (G.arcs[i][j] != defaultWeight) {
return j;
}
}
return 0;
}
/** 返回与顶点vex1邻接的另一个邻接点,没有就返回0 */
int SecondAdjVex_AMG(MatrixGraph G, char* vex1, char* vex2) {
int index1 = LocateVex(&G, vex1);
int index2 = LocateVex(&G, vex2);
if (index1 == -1 || index2 == -1) return 0;
int defaultWeight;
defaultWeight = G.kind <= 1 ? 0 : INT_MAX;
for (int i = index2 + 1; i < G.verTexCount; i++) {
if (G.arcs[index1][i] != defaultWeight) {
return i;
}
}
return 0;
}
/** 广度优先搜索的核心算法 - index为广度优先搜索的某个顶点下标 */
void BFS_AMG(MatrixGraph G, int index) {
printf(" -> %s", G.verTexs[index]);
visited[index] = 1; //设置顶点状态为已访问
SeqQueue queue;
initseqqueue(&queue);
//将当前顶点入队
OfferSeqQueue(&queue, G.verTexs[index]);
while (queue.front != queue.rear) {
//取出队头元素,遍历队头顶点的所有邻接点
char* vex; //取出的队头顶点
PollSeqQueue(&queue, &vex);
for (int i = FirstAdjVex_AMG(G, vex); i; i = SecondAdjVex_AMG(G, vex, G.verTexs[i])) {
if (!visited[i]) {
printf(" -> %s", G.verTexs[i]);
visited[i] = 1; //设置顶点状态为已访问
OfferSeqQueue(&queue, G.verTexs[i]);
}
}
}
}
/** 邻接矩阵的广度优先遍历 */
void BFSTraverse_AMG(MatrixGraph G) {
//初始化状态数组
for (int i = 0; i < G.verTexCount; i++) {
visited[i] = 0;
}
//循环遍历每个顶点
for (int i = 0; i < G.verTexCount; i++) {
if (!visited[i]) {
BFS_AMG(G, i);
}
}
}