题目名称:一维数组的最大子数组和
时间限制:1000ms内存限制:256M
题目描述
下面是一个一维数组的 “最大子数组的和” 的动态规划的解法
# include <iostream>
# include <stdio.h>
# include <string.h>
int MaxSum(int* arr, int size)
{
int current = arr[0]; //current max sum
int max = current;
for (int i = 0; i < size; i++)
{
if (current < 0)
current = 0;
current += arr[i];
if (current > max)
max = current;
}
return max;
}
int main(void)
{
char x[40], y[40];
int a1[5] = { -1, 5, 6, -7, 3 };
int a2[5] = { -5, -4, -8, -1, -10 };
int a3[5] = { -1, 5, 6, -7, 10 };
int max1, max2, max3;
max1 = MaxSum(a1, 5);
max2 = MaxSum(a2, 5); //这个应该返回 -1,
max3 = MaxSum(a3, 5);
}
如果我需要返回值返回这个最大子数组的开始和结束的下标,你要怎么修改这个程序?
输入描述:
第一行输入一个整数n,表示数组长度(n < 100000) 第二行输入数组元素
输出描述:
输出和最大的子数组的开始下标、结束下标
示例
示例1
输入
9
-2 1 -3 4 -1 2 1 -5 4
输出
3 6
提示
解释:连续子数组 [4,-1,2,1] 的和最大,该子数组在原数组中开始下标为 3, 结束下标为 6。
刚看到这个题目的时候,先想的是暴力算法,直接穷举,用递归枚举出所有的连续片段和,取最大的。。。。嗯,结果大家都能想的到,肯定无法通过
这里放出一个提交的用例测试
输入
1000
-6 7 -4 2 -5 2 -4 -7 -3 -9 7 0 7 -8 -7 -10 -5 6 1 -8 9 5 4 6 8 6 -5 -6 -3 5 9 -10 -3 -2 -4 -4 -3 -8 7 5 -6 1 5 -8 -5 6 4 -1 -2 -3 -6 4 -5 -8 8 5 7 1 3 5 9 -6 0 6 0 -7 1 8 0 -6 -6 -3 -1 -4 -2 -10 -2 6 4 -5 -6 0 0 2 6 -4 -6 2 3 -4 7 7 -8 -6 -1 -9 -9 -2 3 -6 -10 -6 9 -5 9 4 5 -3 2 0 3 -2 5 -9 -3 -5 -3 -3 -8 -8 -9 2 0 -4 -6 -5 5 4 -2 -3 7 -6 7 -9 2 -3 -3 -5 4 -5 6 -6 -2 9 -9 5 1 -4 -9 -8 5 1 -6 1 2 8 9 -6 -8 7 -3 -7 7 9 5 -5 6 -10 6 7 -1 -7 6 -7 9 2 3 -9 -1 6 9 -9 1 -6 4 -2 2 9 2 -9 4 5 9 -3 -8 3 7 5 5 9 -4 7 -8 2 3 5 2 -3 -8 4 -6 6 0 -9 8 7 9 4 -10 3 1 -5 8 3 -9 6 4 -8 1 1 0 -10 5 -1 -7 9 3 -6 2 5 -7 -7 7 -5 -4 9 -2 -4 5 -8 6 9 5 -8 -9 -2 1 3 -9 -8 0 2 2 -1 0 4 -2 -10 -3 3 7 -4 1 -4 -7 5 1 9 9 -8 -3 2 -2 -7 9 -7 -8 -10 0 9 9 9 -5 -7 5 5 -9 2 4 -6 -7 5 4 6 9 6 0 3 2 7 -4 5 -6 8 1 -2 -6 -10 -1 -9 4 9 -1 -9 2 -8 -8 -2 -7 6 -5 -1 8 8 -5 -10 -8 -3 1 -1 -3 -7 7 -7 -9 1 2 7 6 -8 -1 3 -2 -6 9 -1 -7 -10 5 7 -4 4 2 4 -2 1 4 8 8 -6 -5 5 -7 -6 9 3 -1 0 9 6 7 7 -7 -8 6 9 -1 -6 7 9 -9 4 0 -2 -7 7 6 6 9 0 -8 9 -10 -10 8 -10 -6 9 8 -6 -9 6 7 4 8 -7 -10 6 -7 7 2 5 0 -6 -2 5 -6 -1 -6 8 -10 -9 5 -7 -9 -4 2 -2 -2 1 -4 -5 6 9 5 3 -7 -6 -6 -9 -6 -1 1 9 -3 -10 8 3 -7 2 4 -6 -1 4 -5 8 3 5 -8 -7 -2 -7 1 -7 6 -8 0 1 -8 -10 6 2 -4 -3 7 1 -6 5 7 -3 -7 3 1 4 4 7 -1 0 7 -1 8 -4 4 9 -10 3 3 7 2 -2 4 -8 5 1 -3 -8 -8 7 0 -1 -4 0 7 4 6 5 -2 -7 -9 1 -9 1 -4 -7 0 -10 -5 -4 4 1 -2 2 8 -9 5 -5 -6 4 9 6 4 -6 -8 -1 8 8 4 3 -6 -4 0 -4 2 -1 -3 7 0 -10 4 6 7 -7 -10 4 -1 7 -4 0 -10 6 4 -9 -8 4 0 -1 6 -10 5 -9 -1 -2 -2 -1 1 -2 -9 -10 -6 8 -10 -9 -2 -7 -9 8 9 -4 8 7 4 -6 -8 4 -10 9 8 9 -5 -4 -2 1 8 -7 1 -8 5 -8 3 9 -6 -1 -5 -4 -2 9 0 2 -8 7 -6 -5 3 2 -7 1 -6 7 2 -9 1 0 -8 -7 -6 4 -5 4 0 9 9 -3 5 -10 1 2 8 -9 -5 3 -9 5 -10 -10 -1 -4 8 -6 7 1 -5 -7 9 6 -6 6 3 -2 -10 8 7 1 -3 2 -8 0 7 9 -9 1 7 4 9 7 -1 4 -1 -3 -8 1 -1 6 0 -5 3 1 -7 -9 5 -10 6 6 9 8 -1 1 -7 8 0 -1 2 1 -2 -6 0 -8 -9 -5 1 -7 8 5 7 -10 -7 5 0 3 3 8 2 -3 -1 9 -1 0 -3 9 -5 0 -1 8 -3 -10 -4 9 -1 7 1 -1 -6 1 3 1 -1 0 2 -3 -1 -2 2 -7 -1 9 6 -1 4 4 5 4 -10 -8 -8 8 -6 5 -6 -10 6 3 -8 -4 1 7 -3 -10 -4 2 -8 -8 -6 -7 8 2 -9 2 0 6 5 3 -7 6 -2 3 5 -5 0 -7 -6 -1 9 6 -6 -7 9 -8 -9 3 -5 -5 -7 7 9 -5 -4 -1 -10 2 9 4 -2 -2 0 -5 5 -6 3 -9 -9 3 4 9 4 2 0 -3 -6 -5 -8 -1 -6 7 5 -3 1 -4 -8 3 2 6 3 2 -10 -5 -8 -6 -3 9 7 6 -6 -3 -7 0 8 -8 7 8 -6 -1 -9 -9 -7 0 -6 -8 -9 6 5 -10 -6 4 0 -10 9 1 -3 0 4 -7 -7 3 9 -4 -1 -1 3 2 -9 -6 -4 -9 5 -10 -3 2 0 0 6 0 -4 -4 1 -6 -10 5 -6 -1 -6 -3 -4 2 9 7 -1 -8 -7 1 -2 -1 -10 -1 -6 -5 7 8 -10 -5 6 -6 -6 9 1 4 -10 -5 5 2 7 0 2 7 5 0 8 9 7 -2 -7 9 -7 -5 -9 4 4 9 -2 7 2 9
呵呵,这要是递归出来,算法复杂度该是多少
然后,老顾当初还没看到背包问题,就自己琢磨了一个办法
将连续的非负整数合并成一个正数,将连续的非正正数合并成一个负数,并记录下合并时的位置信息
然后将首尾两端的负数去掉
例如
10
-3 -7 10 -3 -4 11 12 -4 3 -2
合并后
-10 10 -7 23 -4 3 -2
去掉首尾的负数
10 -7 23 -4 3
然后再枚举也还是很复杂,于是老顾有补充了一个办法,将连续三个数,两边绝对值大于中间数的,合并
10 -7 23 -4 3
合并成
23 -4 3
好像数组中还是很多,嗯再补充一个办法
数组中前两个值得和为负数,或者最后两个数的和为负数的也干掉
嗯,这样,经过递归,最后返回的值就一个了。。。。直接返回了23,取得保存的相应的位置信息,就可以得到题目要求的返回值了
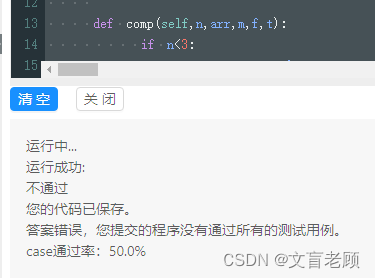
这个办法。。。怎么说呢,是一个土办法,额外记录的东西太多了,有点累赘,算法上倒是复杂度比较低,最后得到了50%的通过率,嗯这里主要存在一个问题,就是最大和的前边有和为零的正负数组合时,我这边是没有放到序列里的,懒得改了。。。
先放出这个土办法的代码
# 请关闭中文输入法,用英文的字母和标点符号。
# 如果你想运行系统测试用例,请点击【执行代码】按钮,如果你想提交作答结果,请点击【提交】按钮,
# 注意:除答案外,请不要打印其他任何多余的字符,以免影响结果验证
# 本OJ系统是基于 OxCoder 技术开发,网址:www.oxcoder.com
# 模版代码提供基本的输入输出框架,可按个人代码习惯修改
class Solution:
def __init__(self) -> None:
self.printAble = False
pass
def comp(self,n,arr,m,f,t):
if n<3:
return arr,m,f,t
x = arr
if x[-1]['s']+x[-2]['s']<=0 and x[-1]['s']<m:
if self.printAble:
print('removed end:',x[-1],x[-2])
x.pop(-1)
x.pop(-1)
return x,m,f,t
if x[0]['s']+x[1]['s']<=0 and x[0]['s']<m:
if self.printAble:
print('removed head:',x[0],x[1])
x.pop(0)
x.pop(0)
return x,m,f,t
l = len(x)
s = 0
while True:
if s+2<len(x):
if x[s]['s']>0 and x[s]['s']+x[s+1]['s']>0 and x[s+2]['s']+x[s+1]['s']>0:
x[s]['e']=x[s+2]['e']
x[s]['a']+=x[s+1]['a']+x[s+2]['a']
x[s]['s']=sum(x[s]['a'])
if m<x[s]['s']:
m=x[s]['s']
f=str(x[s]['b'])
t=str(x[s]['e']-1)
if self.printAble:
print('comp++:{},{}\n{}'.format(x[s+1],x[s+2],x[s]))
x.pop(s+1)
x.pop(s+1)
if x[s]['s']<0 and abs(x[s]['s'])>=x[s+1]['s'] and abs(x[s+2]['s'])>=x[s+1]['s']:
x[s]['e']=x[s+2]['e']
x[s]['a']+=x[s+1]['a']+x[s+2]['a']
x[s]['s']=sum(x[s]['a'])
if self.printAble:
print('comp--:{},{}\n{}'.format(x[s+1],x[s+2],x[s]))
x.pop(s+1)
x.pop(s+1)
s+=1
else:
if l==len(x):
break
else:
l=len(x)
s=0
return x,m,f,t
def solution(self, n, arr):
result = None
# TODO: 请在此编写代码
x = [{'b':0,'e':1,'s':arr[0],'a':[arr[0]]}]
m = 0
rx = ''
ry = ''
for i in range(1,n):
if arr[i]>=0 and x[-1]['s']>0:
x[-1]['e']=i+1
x[-1]['s']+=arr[i]
x[-1]['a'].append(arr[i])
elif arr[i]<=0 and x[-1]['s']<0:
x[-1]['e']=i+1
x[-1]['s']+=arr[i]
x[-1]['a'].append(arr[i])
else:
x.append({'b':i,'e':i+1,'s':arr[i],'a':[arr[i]]})
if m<x[-1]['s']:
m = x[-1]['s']
rx = str(x[-1]['b'])
ry = str(x[-1]['e']-1)
if x[0]['s']<0:
x.pop(0)
if x[-1]['s']<0:
x.pop(-1)
while True:
l = len(x)
x,m,rx,ry = self.comp(l,x,m,rx,ry)
if l == len(x):
break
if self.printAble:
print('\n------\n')
print(x)
result = [rx,ry]
inp = ','.join([str(t) for t in arr])
return result
if __name__ == "__main__":
n = int(input().strip())
arr = [int(item) for item in input().strip().split()]
sol = Solution()
result = sol.solution(n, arr)
print(" ".join(result))
后来,在每日一练中,碰到了一个背包问题,然后被这个算法惊了呆
用了一个二维数组,就将所有可能的最大价值弄出来了。。。。。很不错
为了锻炼孩子的耐心和细心,我还把这个办法教给了孩子,然后和孩子一起填表格玩。。。。。
然后,又在每日一练的选择题里,碰到了一个求一个数组中连续片段最大积的问题。。。。竟然也是用一个二维表格完成的。。。。虽然没要求输出位置,但是很有启发啊!!!
于是,老顾自己也来个二维表格求连续最大和,以及他的位置!!!
def solution(self, n, arr):
result = []
z = [i for i in arr if i>0]
if len(z)<2:
mx = max(arr)
return [str(arr.index(mx)),str(arr.index(mx))]
l = len(arr)
dp = [[0]*(l+1) for _ in range(n)]
dp[0][0] = arr[0]
for i in range(1,l):
dp[i][0] = arr[i]
for j in range(i):
dp[i][j+1] = arr[i] + dp[i-1][j]
rows = [max(row) for row in dp]
mx = max(rows)
row = rows.index(mx)
nums = dp[row].count(mx)
col = dp[row].index(mx)
while nums>1:
col = dp[row].index(mx,col+1)
nums-=1
result = [str(row-col),str(row)]
既然二维数组这么好用,那么我也来一次,第一列放数组本身的数字
第二列放与之前的数的和
arr[0]
arr[1] arr[0]+arr[1]
arr[2] arr[1]+arr[2] arr[0]+arr[1]+arr[2]
…
弄成这么个二维数组后,直接看哪个数组的最大值最大,那么和最大的就在那个行里了,第一个下标就是结尾数字的位置了,然后如果出现了多次最大值,取靠后的那个,然后得到该最大值所在列的位置,然后行减去列,就是开始位置了。。。。这么一看,简直简单的一批。。。。土办法什么的真弱。。。。。
真是不学不知道,原来老顾已经落伍的这么严重了