集合
1、集合中的数据元素除了属于同一集合外,没有任何的逻辑关系
2、在集合中,每个数据元素都有一个区别于其他元素的唯一标识(键值或者关键字值)
3、集合的运算:
1 查找某一元素是否存在(内部查找、外部查找)
2 将集合中的元素按照它的唯一标识进行排序
4、集合的存储:
1 任何容器都可以存储集合
2 常用的表示形式是借鉴于线性表或树
5、唯一 一个仅适合于存储和处理集合的数据结构是散列表
注意:
散列表不但是一种存储方法也是一种查找方法
查找
1、查找表:用于查找的集合称为查找表
2、查找表的分类:
1 静态查找表:其中的元素是静态的(不会动态变化)
2 动态查找表:其中的元素经常进行插入和删除操作(会动态变化)
3、平均查找长度:是指查找过程中对关键码的平均比较次数

注意:顺序查找从左到右
顺序查找(无序表)
毫无选择只能做线性的顺序查找

注意:监视哨在data[0]的位置

核心步骤:(一定是可以找到该元素的)
int i;
data[0] = k;
//从后往前查找
for(i=data.size()-1;k!=data[i];--i)
return i;
//查找成功返回该元素的对应下标
//查找失败返回0(在下标为0的位置找到该元素)
顺序查找(有序表)
和无序表的顺序查找是类似的,只是当被查找元素在表中不存在的时候,不需要遍历到表尾
例如:在0 2 4 6 8 中查找5的时候,从后往前遍历,走到4的时候就可以结束遍历

核心步骤:
int i;
data[0] = k;
//从后往前查找
for(i=data.size()-1;k<data[i];--i)
if(k == data[i]) return i;
return 0;
无序表的顺序查找的平均查找长度(ASL)
注意:从后往前进行比较
推导:
1 查找第一个元素需要比较n次
2 查找第二个元素需要比较n-1次
3 ...
4 查找第n个元素需要比较1次
5 那么总共需要比较n*(n+1)/2
6 假设每个关键码都是等概率的:p = 1/n
7 那么n*(n+1)/2 * 1/n = (n+1)/2
8 也就是说:在查找成功的情况下平均需要比较(n+1)/2个元素


注意:n*(n+1)*(1/n) = (n+1)
1 查找每个元素都需要从末尾比较到0
该算法的时间复杂度为O(n)

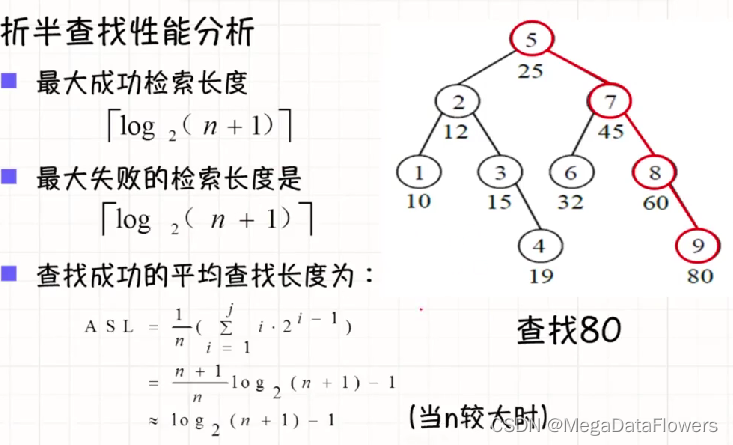
折半查找(二分查找)


查找成功:

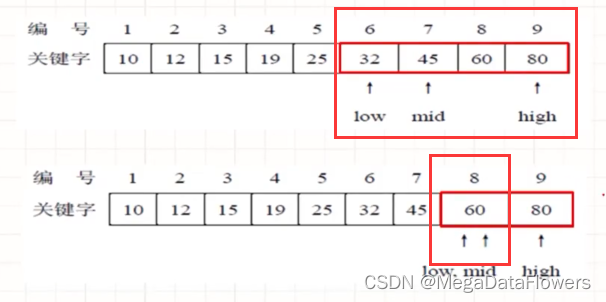
查找失败:


非递归折半查找:

int low = 1;
int high = data.size()-1;
int mid;
while(low<=high)
{
mid = (low+high)/2;
if(k == data[mid]) return mid;
if(k<data[mid]) high = mid-1;
else low = mid+1;
}
return 0;

递归折半查找:

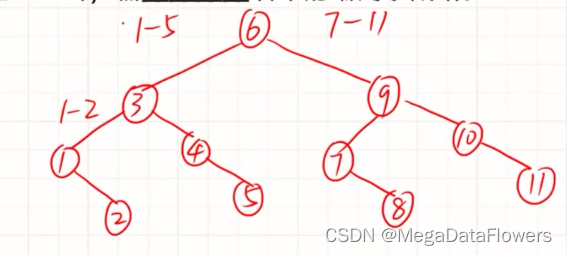
折半查找(判定树)

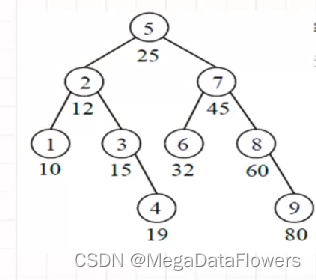
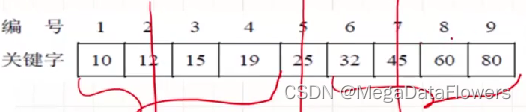
注意:
对判定树进行中序遍历得到的序列和有序表一样
外部结点和内部结点:
注意:
1 外部结点数目 = 内部结点数目 + 1
2 外部结点都是叶子结点
3 内部结点都是度为2的结点
4 n0 = n2 + 1
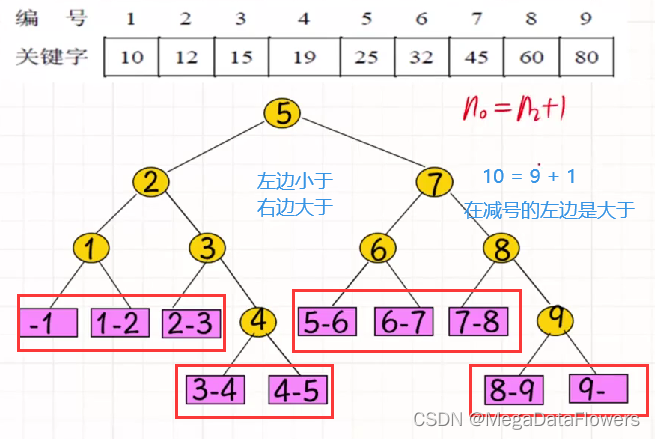
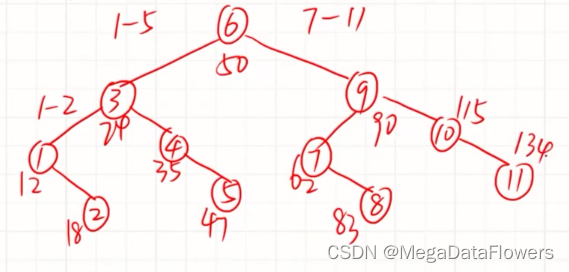
计算平均查找长度:
1 查找成功(内部结点):(1*1+2*2+3*4+4*2)/9 = 25/9
2 查找失败(外部结点):(3*6+4*4)/10 = 34/100

折半查找的性能:

分块查找(索引顺序块的查找)

注意:
1 块之间是有序的(第一块所有值小于第二块的所有值...)
2 在块内的元素之间可能有序也可能无序
索引表:
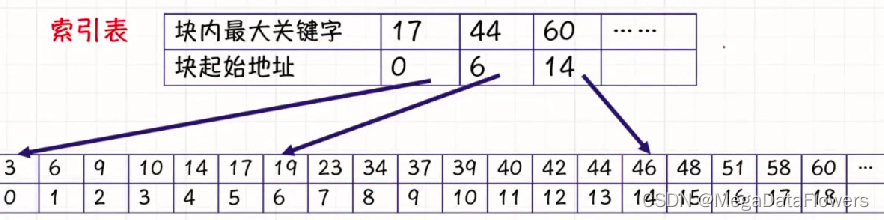

注意:
1 先在索引表内查找
2 在对应块内的查找
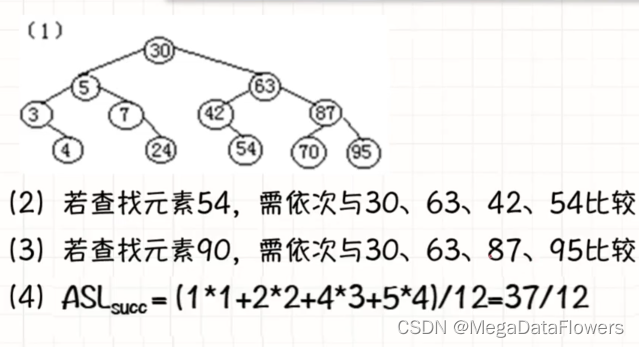
典型题目解析

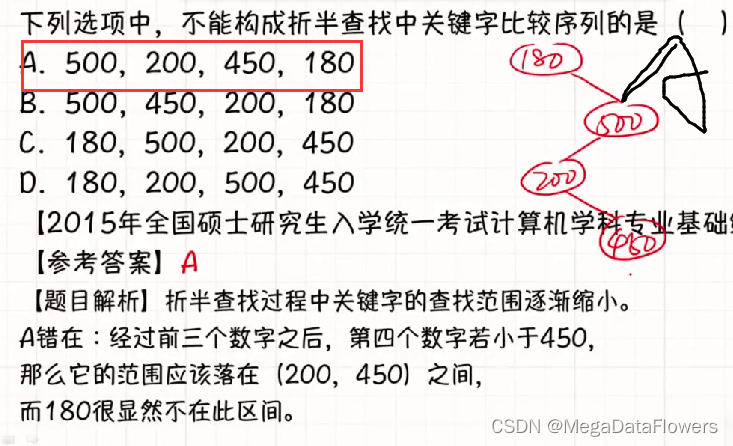
解释:
1 左边是小于
2 右边是大于
3 判断是否为一条直线
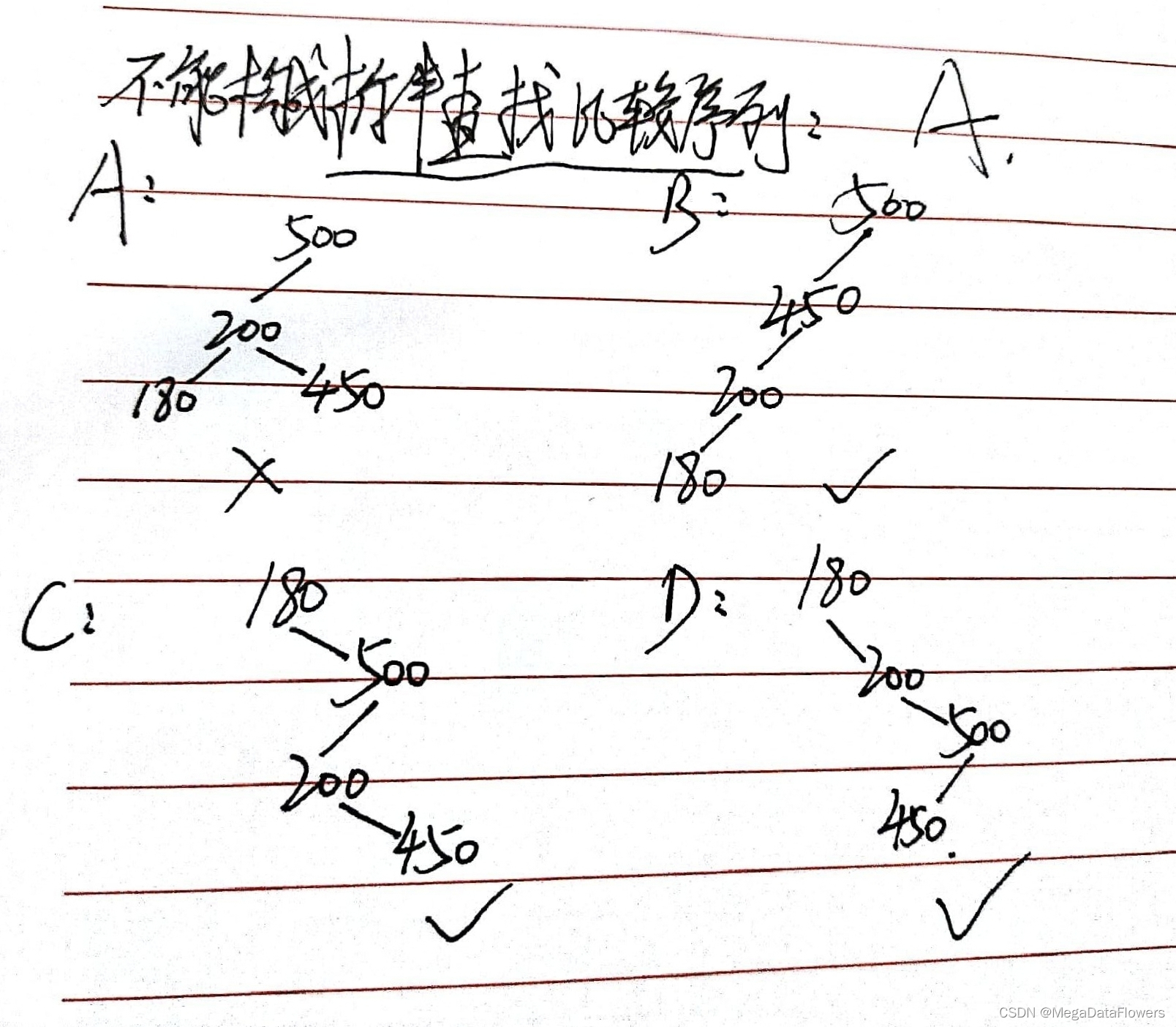

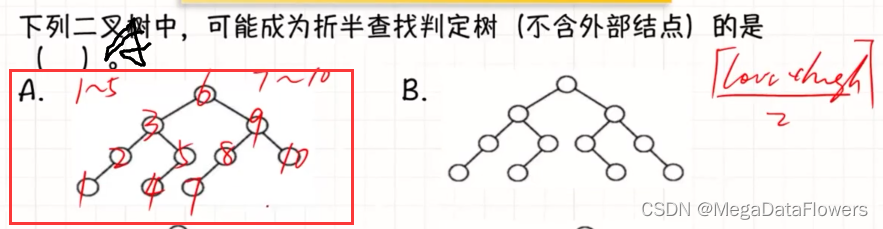

注意:
左分支高度大于等于右分支(向上取整)
易错题

注意:折半查找判定树的高度和完全二叉树的高度是一致的
1 向下取整:**右分支的长度大于等于左分支的长度**
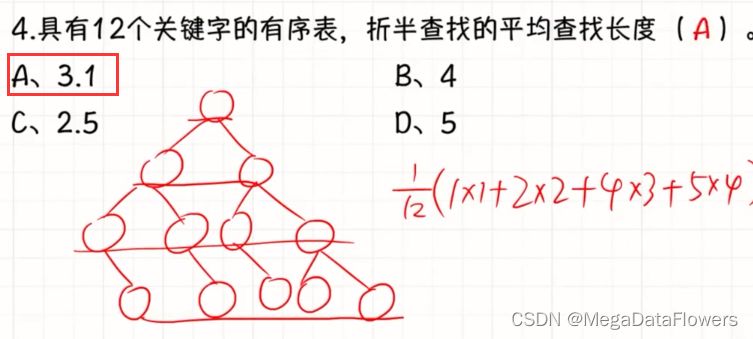



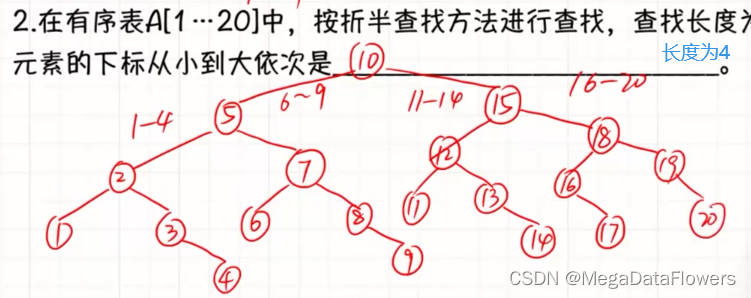

答案为:
1 3 6 8 11 13 16 19