一、回归问题概述

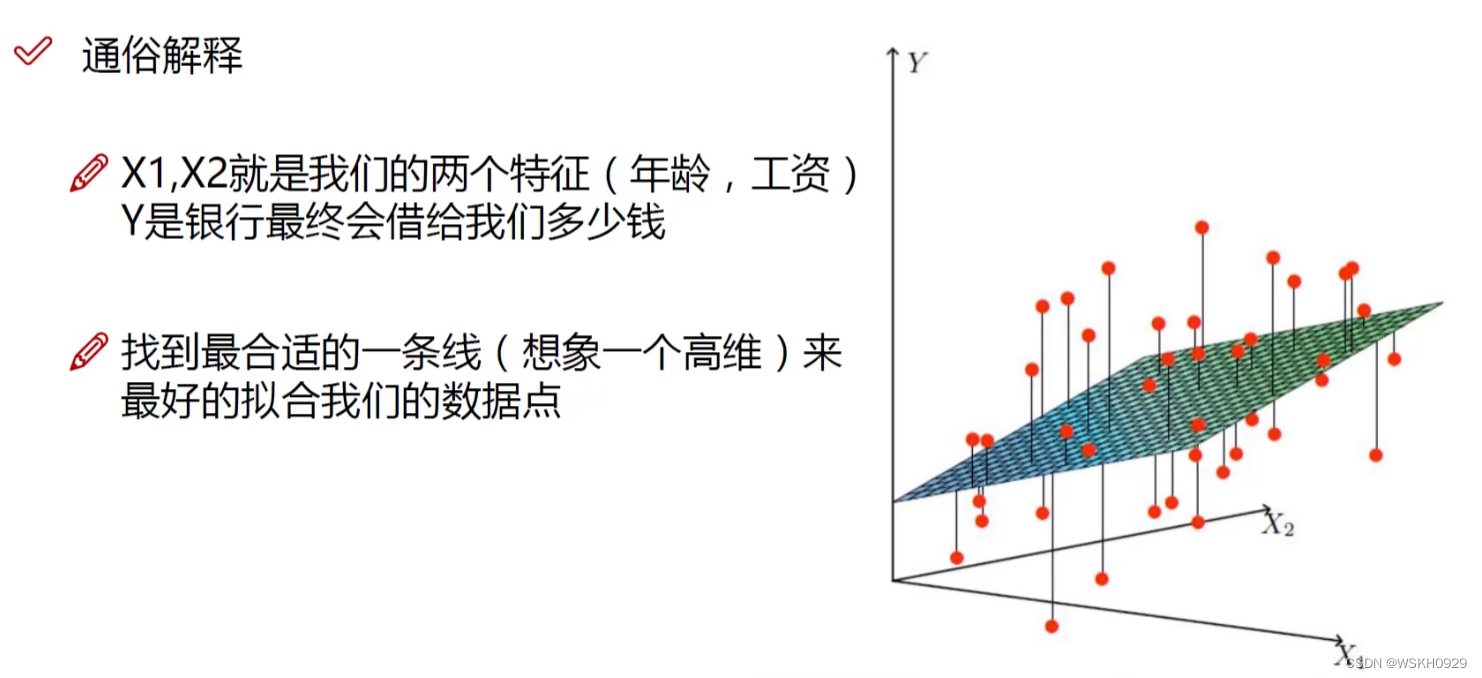
回归：根据工资和年龄，预测额度为多少
其中，工资和年龄被称为特征（自变量），额度被称为标签（因变量）

在这里插入图片描述

下图展示了线性回归特性，其相当于Y = aX1+bX2+c，在此问题中，就相当于一个三维空间中的二维平>面，我们希望找到一个二维平面，尽可能接近所有点

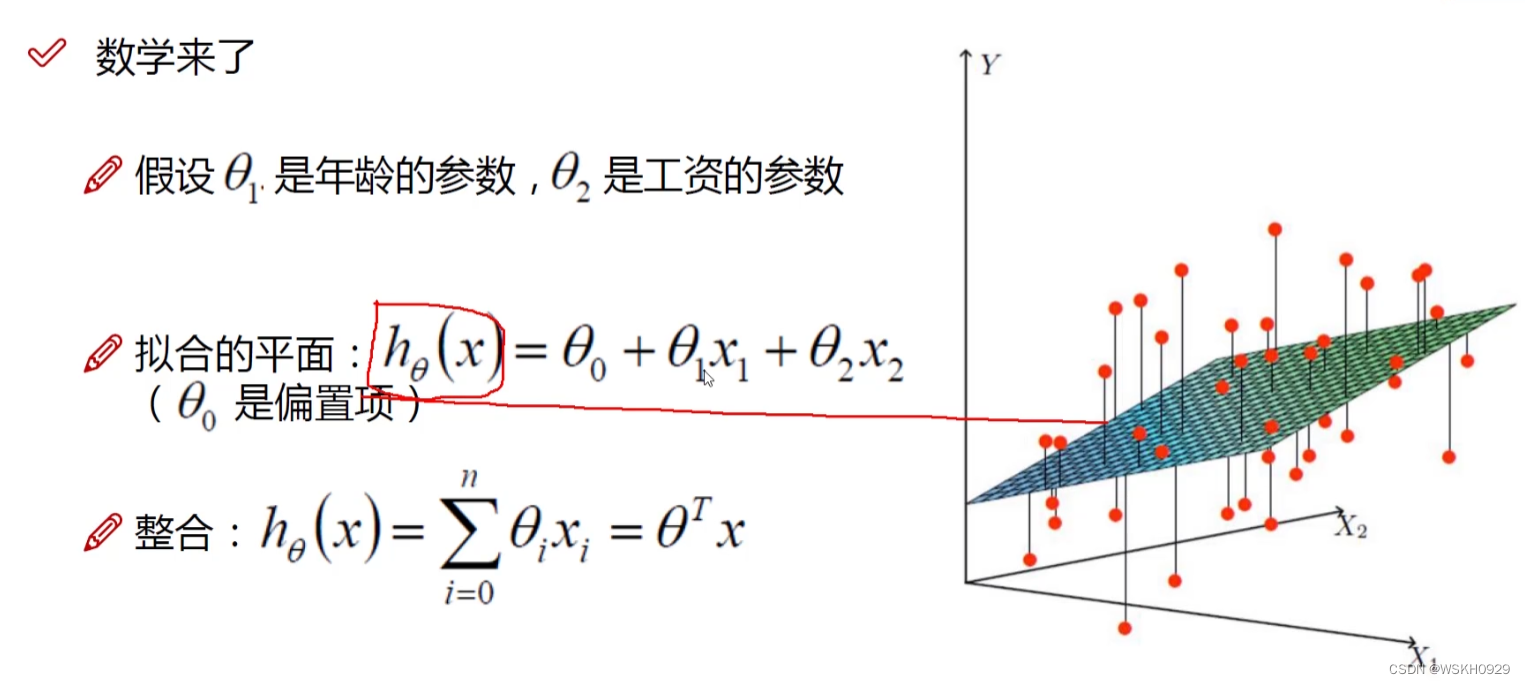
在这里插入图片描述

二、误差项定义

在这里插入图片描述

下图展示了误差项的定义，我们一般认为误差项越接近0越好

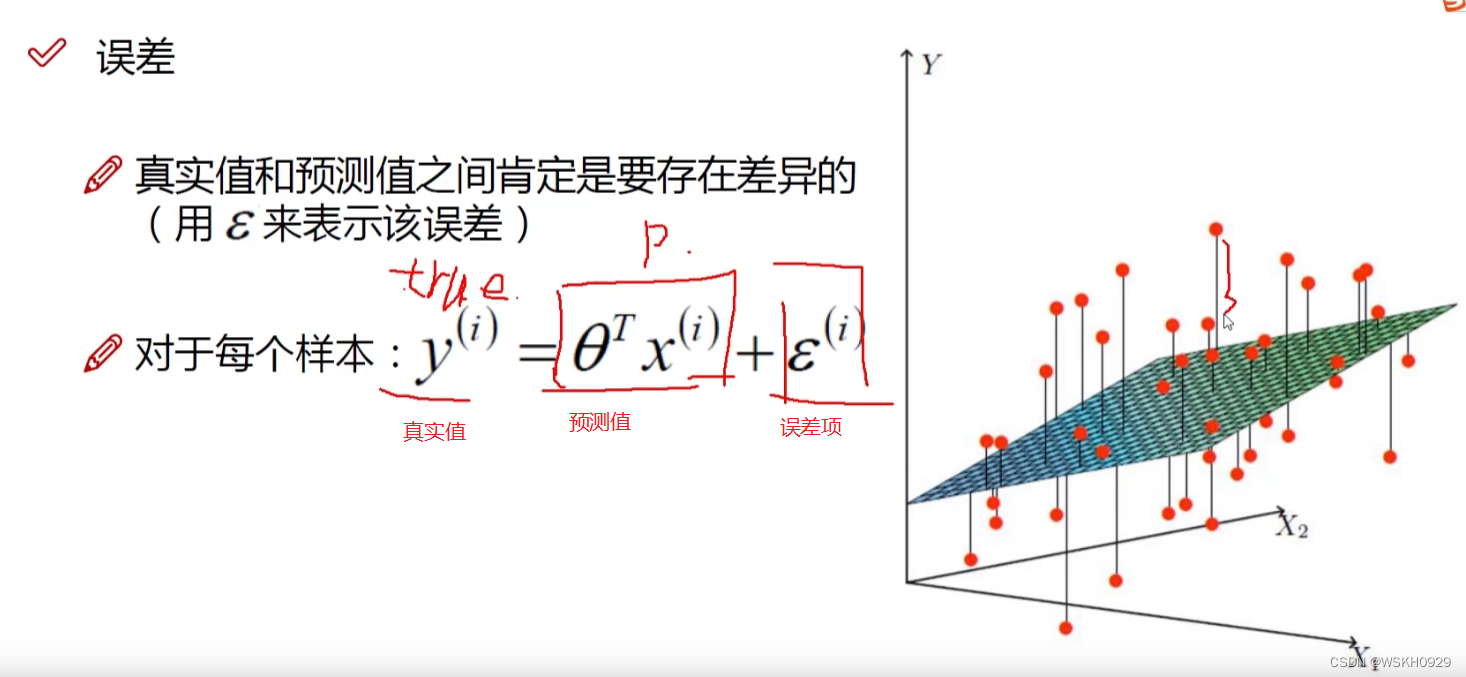
在这里插入图片描述

三、独立同分布的假设

误差 $\varepsilon^{(i)}$ 是独立并且具有相同的分布，并且服从均值为0方差为 $\boldsymbol{\theta}^2$ 的高斯分布
独立：张三和李四一起来贷款，他俩没关系
同分布: 他俩都来得是我们假定的这家银行
高斯分布(正态分布) : 银行可能会多给，也可能会少给，但是绝大多数情况下这个浮动不会太大，极小情况下浮动会比较大，符合正常情况

在这里插入图片描述

四、似然函数的作用

(1) 预测值与误差 :

$y^{(i)}=\theta^T x^{(i)}+\varepsilon^{(i)}$

(2) 由于误差服从高斯分布 :

$p\left(\epsilon^{(i)}\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(\epsilon^{(i)}\right)^2}{2 \sigma^2}\right)$

将 $(1)$ 式带入 $(2)$ 式:

$p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right)$

似然函数(独立同分布的前提下，联合概率密度等于边缘概率密度的乘积) :

$L(\theta)=\prod_{i=1}^m p\left(y^{(i)} \mid x^{(i)} ; \theta\right)=\prod_{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right)$

解释 : 什么样的参数跟我们的数据组合后恰好是真实值

对数似然 :

$\log L(\theta)=\log \prod_{i=1}^m \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right)$

解释 : 乘法难解，加法就容易了，对数里面乘法可以转换成加法

五、参数求解

展开化简 :

$\sum_{i=1}^m \log \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y^{(i)}-\theta^T x^{(i)}\right)^2}{2 \sigma^2}\right) \\ =m \log \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{\sigma^2} \cdot \frac{1}{2} \sum_{i=1}^m\left(y^{(i)}-\theta^T x^{(i)}\right)^2$

目标：让似然函数（对数变换后也一样 ) 越大越好

$J(\theta)=\frac{1}{2} \sum_{i=1}^m\left(y^{(i)}-\theta^T x^{(i)}\right)^2 \text { ( 最小二乘法 ) }$

目标函数 :

$J(\theta)=\frac{1}{2} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2=\frac{1}{2}(X \theta-y)^T(X \theta-y)$

求偏导:

$\begin{aligned} \quad \nabla_\theta J(\theta)&=\nabla_\theta\left(\frac{1}{2}(X \theta-y)^T(X \theta-y)\right) \\ &=\nabla_\theta\left(\frac{1}{2}\left(\theta^T X^T-y^T\right)(X \theta-y)\right) \\ &=\nabla_\theta\left(\frac{1}{2}\left(\theta^T X^T X \theta-\theta^T X^T y-y^T X \theta+y^T y\right)\right) \\ &=\frac{1}{2}\left(2 X^T X \theta-X^T y-\left(y^T X\right)^T\right)=X^T X \theta-X^T y \end{aligned}$

偏导等于0:

$\theta=\left(X^T X\right)^{-1} X^T y$

六、梯度下降算法

引入: 当我们得到了一个目标函数后，如何进行求解?
直接求解 ? ( 并不一定可解，线性回归可以当做是一个特例 )

常规套路: 机器学习的套路就是我交给机器一堆数据, 然后告诉它什么样的学习方式是对的（目标函数），然后让它朝着这个方向去做

如何优化: 一口吃不成个胖子，我们要静悄悄的一步步的完成迭代 ( 每次优化一点点，累积起来就是个大成绩了)

在这里插入图片描述

七、参数更新方法

目标函数 :

$J\left(\theta_0, \theta_1\right)=\frac{1}{2 m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2$

寻找山谷的最低点，也就是我们的目标函数终点 ( 什么样的参数能使得目标函数达到极值点)
下山分几步走呢? ( 更新参数 )
(1) : 找到当前最合适的方向
(2) : 走那么一小步，走快了该" 跌倒 "了
(3)：按照方向与步伐去更新我们的参数

批量梯度下降:

$\frac{\partial J(\theta)}{\partial \theta_j}=-\frac{1}{m} \sum_{i=1}^m\left(y^i-h_\theta\left(x^i\right)\right) x_j^i \\ \theta_j^{\prime}=\theta_j+\frac{1}{m} \sum_{i=1}^m\left(y^i-h_\theta\left(x^i\right)\right) x_j^i$