分类预测 | MATLAB实现SSA-CNN麻雀算法优化卷积神经网络多特征分类预测

分类效果

基本介绍

1.Matlab实现SSA-CNN麻雀算法优化卷积神经网络多特征分类预测，运行环境Matlab2018b及以上；
2.运行主程序MainSSA_CNNC即可，其余为函数文件，无需运行，可视化输出分类准确率，可在下载区获取数据和程序内容。
3.输入15个特征，输出4类标签。
4.SSA优化CNN的超参数，一共有9个参数需要优化，分别是学习率、迭代次数、批处理样本、第一层卷积层的核大小和数量、第2层卷积层的核大小和数量，以及两个全连接层的神经元数量。

模型描述

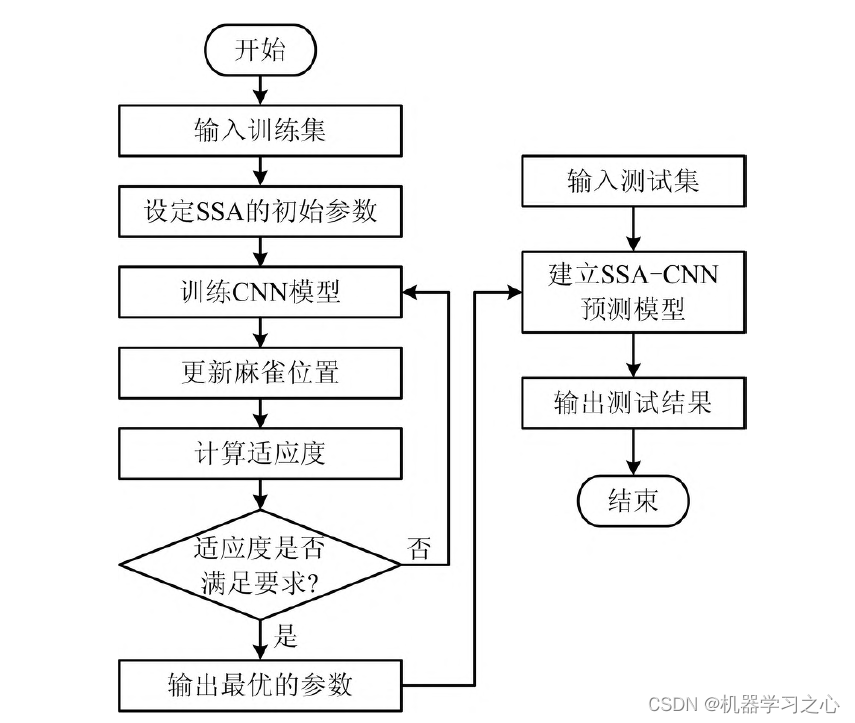
卷积神经网络(CNN)中超参数众多,人工选择比较困难,利用麻雀搜索算法(SSA)对卷积神经网络中的参数进行优化,消除人工操作的不确定性。本模型共优化8 个超参数,分别是迭代次数、学习率、第1 层卷积核大小和数量、第2 层卷积核大小和数量,以及2 个全连接层的神经元数量(conv 表示卷积层,fc 表示全连接层)。本文建立的模型组成包括输入层、2 层卷积层、2 层激活层、2 层全连接层和输出层。SSA CNN 模型预测具体实现步骤如下。
第1 步:对数据进行归一化处理。
第2 步:设定初始参数,包括种群中的个体总数、子群体数、每个子群体中的麻雀数、最大迭代次数、发现者的数量及SSA 其他参数等。
第3 步:初始化种群并定义适应度函数,以CNN的预测值与实际值的均方误差最小化作为适应度函数,SSA 的目的就是找到一组超参数,用这组超参数训练得到的CNN 的误差能够最小化。
第4 步:计算适应度函数值并排序。
第5 步:确定每个子群体中的最优解、最差解和全局最优解。
第6 步:更新麻雀位置,获取当前的新位置,如果新位置比以前的位置更好就更新它,若达到设定的最大迭代次数,则将其输出,否则返回继续寻优,直到得到最好的麻雀坐标。
第7 步:将寻优得到的麻雀坐标代入CNN 模型中,得到预测模型的输出。

程序设计

• 完整程序和数据私信博主。

%种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
%计算初始适应度值
fitness = zeros(1,pop);
for i = 1:pop
   fitness(i) =  fobj(X(i,:));
end
[fitness, index]= sort(fitness);%升排序
BestF = fitness(1);
WorstF = fitness(end);
GBestF = fitness(1);%全局最优适应度值
for i = 1:pop
    X(i,:) = X0(index(i),:);
end
curve=zeros(1,Max_iter);
GBestX = X(1,:);%全局最优位置
X_new = X;
for i = 1: Max_iter
    
    disp(['第',num2str(i),'次迭代'])
    BestF = fitness(1);
    WorstF = fitness(end);

    
    R2 = rand(1);
   for j = 1:PDNumber
      if(R2<ST)
          X_new(j,:) = X(j,:).*exp(-j/(rand(1)*Max_iter));
      else
          X_new(j,:) = X(j,:) + randn()*ones(1,dim);
      end     
   end
   for j = PDNumber+1:pop
%        if(j>(pop/2))
        if(j>(pop - PDNumber)/2 + PDNumber)
          X_new(j,:)= randn().*exp((X(end,:) - X(j,:))/j^2);
        else
          %产生-1，1的随机数
          A = ones(1,dim);
          for a = 1:dim
            if(rand()>0.5)
                A(a) = -1;
            end
          end 
          AA = A'*inv(A*A');     
          X_new(j,:)= X(1,:) + abs(X(j,:) - X(1,:)).*AA';
       end
   end
   Temp = randperm(pop);
   SDchooseIndex = Temp(1:SDNumber); 
   for j = 1:SDNumber
       if(fitness(SDchooseIndex(j))>BestF)
           X_new(SDchooseIndex(j),:) = X(1,:) + randn().*abs(X(SDchooseIndex(j),:) - X(1,:));
       elseif(fitness(SDchooseIndex(j))== BestF)
           K = 2*rand() -1;
           X_new(SDchooseIndex(j),:) = X(SDchooseIndex(j),:) + K.*(abs( X(SDchooseIndex(j),:) - X(end,:))./(fitness(SDchooseIndex(j)) - fitness(end) + 10^-8));
       end
   end
  %边界控制
   for j = 1:pop
       for a = 1: dim
           if length(ub)>1
               if(X_new(j,a)>ub(a))
                   X_new(j,a) =ub(a);
               end
               if(X_new(j,a)<lb(a))
                   X_new(j,a) =lb(a);
               end
           else
                if(X_new(j,a)>ub)
                   X_new(j,a) =ub;
               end
               if(X_new(j,a)<lb)
                   X_new(j,a) =lb;
               end
           end
       end
   end 
   %更新位置
   for j=1:pop
     fitness_new(j) = fobj(X_new(j,:));
   end
   for j = 1:pop
    if(fitness_new(j) < GBestF)
       GBestF = fitness_new(j);
        GBestX = X_new(j,:);   
    end
   end
   X = X_new;
   fitness = fitness_new;
    %排序更新
   [fitness, index]= sort(fitness);%排序
   BestF = fitness(1);
   WorstF = fitness(end);
   for j = 1:pop
      X(j,:) = X(index(j),:);
   end
   curve(i) = GBestF;
    disp(['current iteration is: ',num2str(i), ', best fitness is: ', num2str(GBestF)]);
end

参考文献

[1] https://blog.csdn.net/kjm13182345320/article/details/128713044?spm=1001.2014.3001.5501
[2] https://blog.csdn.net/kjm13182345320/article/details/128700127?spm=1001.2014.3001.5501