将两个的有序数列合并成一个有序数列,我们称之为"归并"。归并排序(Merge Sort)就是利用归并思想对数列进行排序。
归并排序介绍
根据具体的实现,归并排序包括"从上往下"和"从下往上"2种方式。
从下往上的归并排序
将待排序的数列分成若干个长度为1的子数列,然后将这些数列两两合并;得到若干个长度为2的有序数列,再将这些数列两两合并;得到若干个长度为4的有序数列,再将它们两两合并;直接合并成一个数列为止。这样就得到了我们想要的排序结果。(参考下面的图片)
从上往下的归并排序
它与"从下往上"在排序上是反方向的。它基本包括3步:
分解 -- 将当前区间一分为二,即求分裂点 mid = (low + high)/2;
求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。
合并 -- 将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。
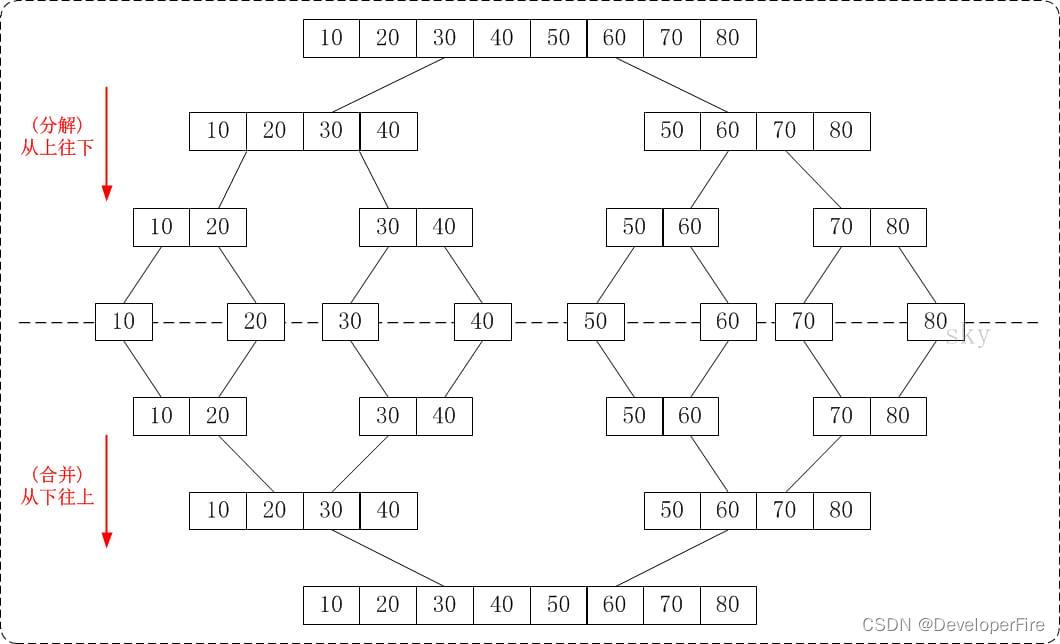
归并排序实现
从上往下的归并排序
从上往下的归并排序采用了递归的方式实现。它的原理非常简单,如下图:
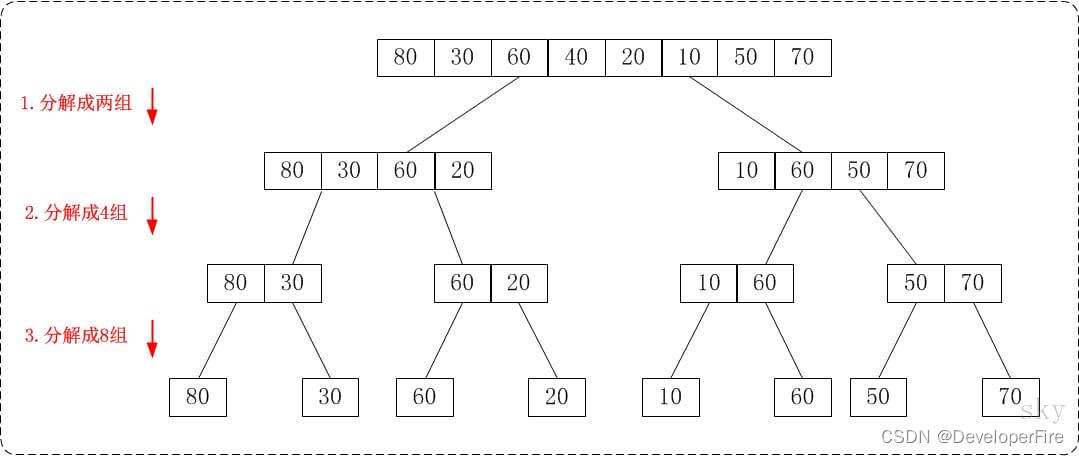
通过"从上往下的归并排序"来对数组{80,30,60,40,20,10,50,70}进行排序时:
将数组{80,30,60,40,20,10,50,70}看作由两个有序的子数组{80,30,60,40}和{20,10,50,70}组成。对两个有序子树组进行排序即可。
将子数组{80,30,60,40}看作由两个有序的子数组{80,30}和{60,40}组成。
将子数组{20,10,50,70}看作由两个有序的子数组{20,10}和{50,70}组成。
将子数组{80,30}看作由两个有序的子数组{80}和{30}组成。
将子数组{60,40}看作由两个有序的子数组{60}和{40}组成。
将子数组{20,10}看作由两个有序的子数组{20}和{10}组成。
将子数组{50,70}看作由两个有序的子数组{50}和{70}组成。
从下往上的归并排序
从下往上的归并排序的思想正好与"从下往上的归并排序"相反。如下图:
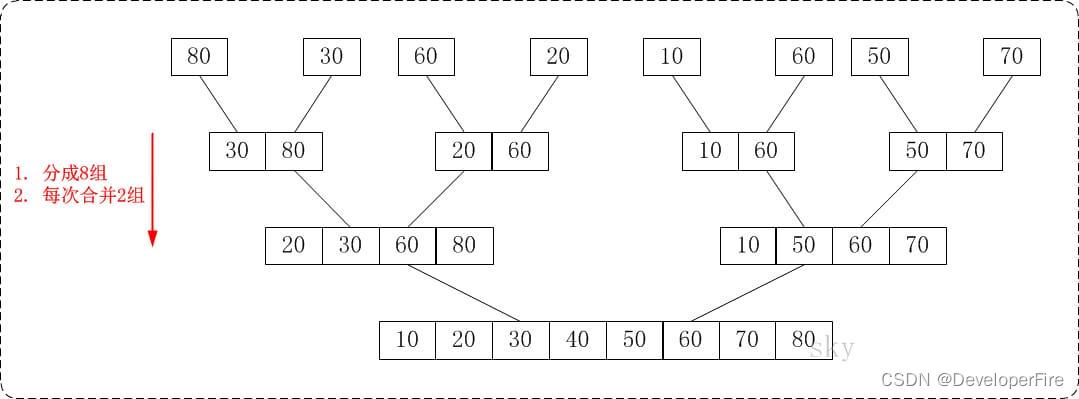
通过"从下往上的归并排序"来对数组{80,30,60,40,20,10,50,70}进行排序时:
将数组{80,30,60,40,20,10,50,70}看作由8个有序的子数组{80},{30},{60},{40},{20},{10},{50}和{70}组成。
将这8个有序的子数列两两合并。得到4个有序的子树列{30,80},{40,60},{10,20}和{50,70}。
将这4个有序的子数列两两合并。得到2个有序的子树列{30,40,60,80}和{10,20,50,70}。
将这2个有序的子数列两两合并。得到1个有序的子树列{10,20,30,40,50,60,70,80}。
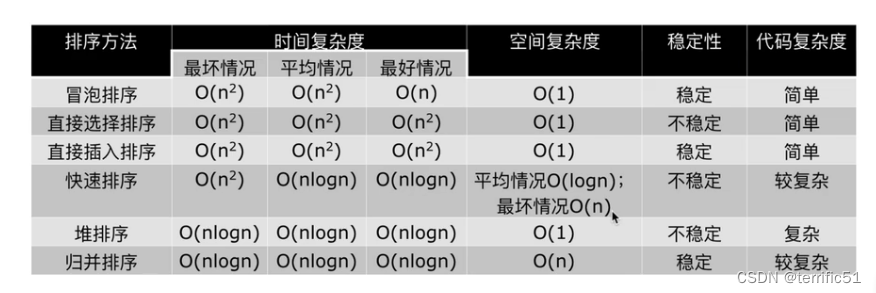
归并排序的时间复杂度和稳定性
归并排序时间复杂度
归并排序的时间复杂度是O(N*lgN)。
假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N),需要遍历多少次呢? 归并排序的形式就是一棵二叉树,它需要遍历的次数就是二叉树的深度,而根据完全二叉树的可以得出它的时间复杂度是O(N*lgN)。
归并排序稳定性
归并排序是稳定的算法,它满足稳定算法的定义。
算法稳定性 -- 假设在数列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;并且排序之后,a[i]仍然在a[j]前面。则这个排序算法是稳定的!
代码实现
/**
* 归并排序: Java
*
* @author skywang
* @date 2014/03/12
*/
public class MergeSort {
/*
* 将一个数组中的两个相邻有序区间合并成一个
*
* 参数说明:
* a -- 包含两个有序区间的数组
* start -- 第1个有序区间的起始地址。
* mid -- 第1个有序区间的结束地址。也是第2个有序区间的起始地址。
* end -- 第2个有序区间的结束地址。
*/
public static void merge(int[] a, int start, int mid, int end) {
int[] tmp = new int[end-start+1]; // tmp是汇总2个有序区的临时区域
int i = start; // 第1个有序区的索引
int j = mid + 1; // 第2个有序区的索引
int k = 0; // 临时区域的索引
while(i <= mid && j <= end) {
if (a[i] <= a[j])
tmp[k++] = a[i++];
else
tmp[k++] = a[j++];
}
while(i <= mid)
tmp[k++] = a[i++];
while(j <= end)
tmp[k++] = a[j++];
// 将排序后的元素,全部都整合到数组a中。
for (i = 0; i < k; i++)
a[start + i] = tmp[i];
tmp=null;
}
/*
* 归并排序(从上往下)
*
* 参数说明:
* a -- 待排序的数组
* start -- 数组的起始地址
* endi -- 数组的结束地址
*/
public static void mergeSortUp2Down(int[] a, int start, int end) {
if(a==null || start >= end)
return ;
int mid = (end + start)/2;
mergeSortUp2Down(a, start, mid); // 递归排序a[start...mid]
mergeSortUp2Down(a, mid+1, end); // 递归排序a[mid+1...end]
// a[start...mid] 和 a[mid...end]是两个有序空间,
// 将它们排序成一个有序空间a[start...end]
merge(a, start, mid, end);
}
/*
* 对数组a做若干次合并: 数组a的总长度为len,将它分为若干个长度为gap的子数组;
* 将"每2个相邻的子数组" 进行合并排序。
*
* 参数说明:
* a -- 待排序的数组
* len -- 数组的长度
* gap -- 子数组的长度
*/
public static void mergeGroups(int[] a, int len, int gap) {
int i;
int twolen = 2 * gap; // 两个相邻的子数组的长度
// 将"每2个相邻的子数组" 进行合并排序。
for(i = 0; i+2*gap-1 < len; i+=(2*gap))
merge(a, i, i+gap-1, i+2*gap-1);
// 若 i+gap-1 < len-1,则剩余一个子数组没有配对。
// 将该子数组合并到已排序的数组中。
if ( i+gap-1 < len-1)
merge(a, i, i + gap - 1, len - 1);
}
/*
* 归并排序(从下往上)
*
* 参数说明:
* a -- 待排序的数组
*/
public static void mergeSortDown2Up(int[] a) {
if (a==null)
return ;
for(int n = 1; n < a.length; n*=2)
mergeGroups(a, a.length, n);
}
public static void main(String[] args) {
int i;
int a[] = {80,30,60,40,20,10,50,70};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
mergeSortUp2Down(a, 0, a.length-1); // 归并排序(从上往下)
//mergeSortDown2Up(a); // 归并排序(从下往上)
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}