背包问题求方案数、具体方案
- 01背包问题求体积恰好等于V的方案数
- 完全背包问题求体积恰好等于V的方案数
- 01背包问题求最优选法的方案数
- 完全背包问题求最优选法的方案数
- 01背包问题求具体方案
01背包问题求体积恰好等于V的方案数
原题链接AcWing278. 数字组合
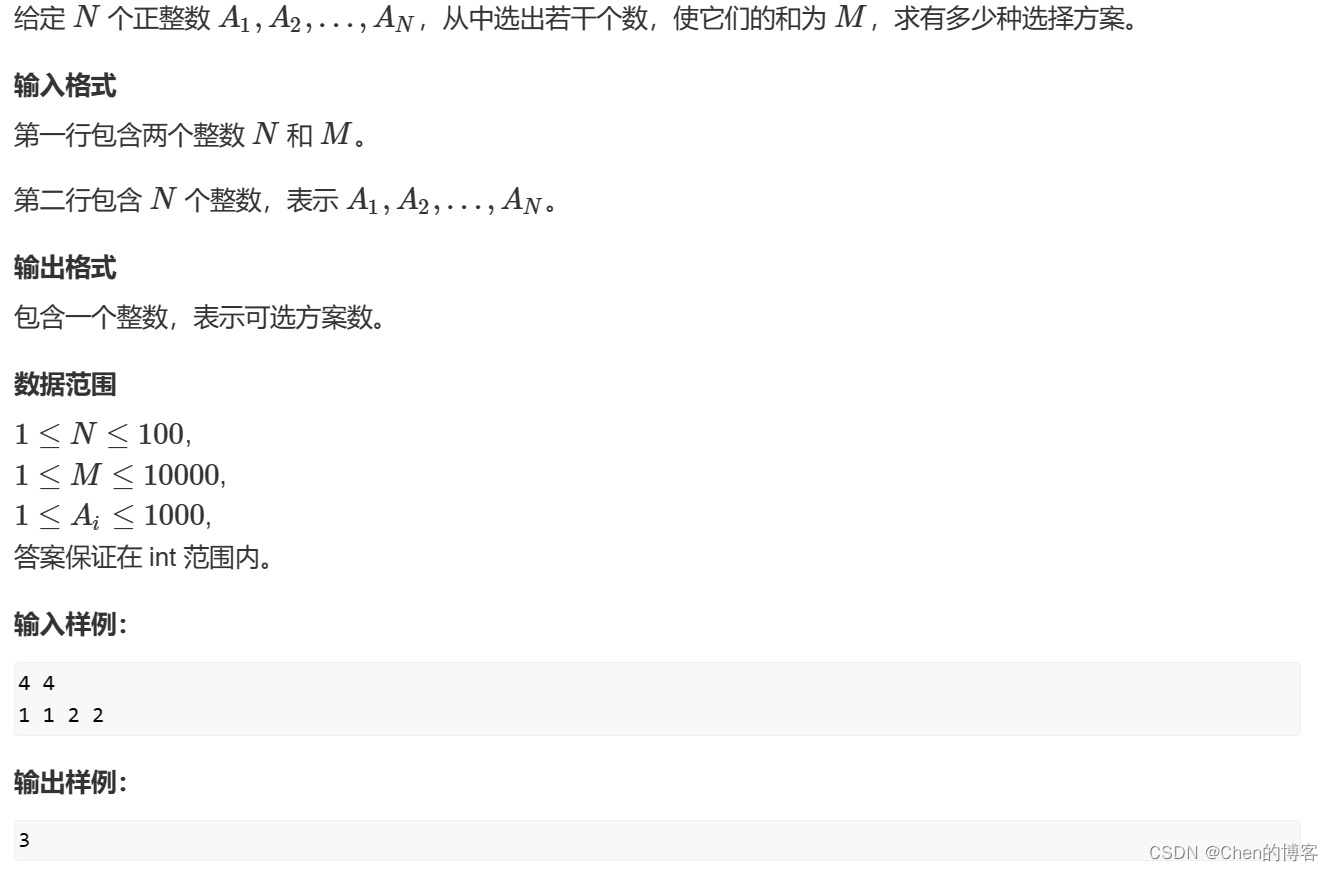
考虑状态表示:
f[i][j]表示考虑前1~i个物品,体积恰好为j时的方案数(不考虑前1~i个物品组合后的价值,只考虑组合后的体积)
状态转移:
可以分两种情况
选第i个物品使得体积为j
不选第i个物品使其体积为j
第i个物品体积为v,价值为w
可以发现f[i][j]由上述两种情况构成,所以
f[i][j]=f[i-1][j]+f[i-1][j-v]
因为是体积恰好是j,所以初始化时
memset(f,0,sizeof f)
f[0][0]=1;
再对空间复杂度进行优化
代码如下:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=10010;
int f[M];//f[i][j]表示考虑前1~i个物品,体积恰好为j时的方案数
int main(){
int n,m;
cin>>n>>m;
f[0]=1;
for(int i=0;i<n;i++){
int v;
scanf("%d",&v);
for(int j=m;j>=v;j--)
f[j]=f[j]+f[j-v];
}
cout<<f[m]<<endl;
return 0;
}
完全背包问题求体积恰好等于V的方案数
原题链接AcWing 1023. 买书

物品数量无限,这是一道完全背包求方案数问题
考虑状态表示:
f[i][j]表示考虑前1~i个物品,体积恰好为j时的方案数(不考虑前1~i个物品组合后的价值,只考虑组合后的体积)
状态转移:
可以分多种情况
不选第i个物品使其体积为j f[i-1][j]
选1个第i个物品使得体积为j f[i-1][j-v]
选2个第i个物品使得体积为j f[i-1][j-2*v]
.....
选s个第i个物品使得体积为j f[i-1][j-s*v]
第i个物品体积为v,价值为w
可以发现f[i][j]由上述s+1种情况构成,所以
f[i][j]=f[i-1][j]+f[i-1][j-v]+f[i-1][j-2*v]+.....+f[i-1][j-s*v]
而
f[i][j-v]=f[i-1][j-v]+f[i-1][j-2*v]+.....+f[i-1][j-s*v]
所以
f[i][j]=f[i-1][j]+f[i][j-v]
因为是体积恰好是j,所以初始化时
memset(f,0,sizeof f)
f[0][0]=1;
再对空间复杂度进行优化
代码如下:
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1010;
int f[N];
int d[4]={10,20,50,100};
int main(){
int n;
cin>>n;
f[0]=1;
for(int i=0;i<4;i++)
for(int j=d[i];j<=n;j++)
f[j]+=f[j-d[i]];
cout<<f[n];
return 0;
}
01背包问题求最优选法的方案数
AcWing 11. 背包问题求方案数

考虑状态表示:
f[i][j]表示考虑前1~i个物品, 体积恰好为j时的最大价值
g[i][j]表示考虑前1~i个物品,体积恰好为j时(最大价值)时的方案数
状态转移:
可以分两种情况
选第i个物品使得体积为j
不选第i个物品使其体积为j
第i个物品体积为v,价值为w
可以发现f[i][j]由上述两种情况构成,所以
f[i][j]=max(f[i-1][j],f[i-1][j-v]+w)
f[i-1][j]==f[i-1][j-v]+w时,g[i][j]=g[i-1][j-v]+g[i-1][j]//选不选i都行,可以从两种状态转移而来
f[i-1][j]<f[i-1][j-v]+w时,g[i][j]=g[i-1][j-v]//考虑要求最大价值时的方案数,只能从一种状态转移而来
f[i-1][j]>f[i-1][j-v]+w时,g[i][j]=g[i-1][j]//考虑要求最大价值时的方案数,只能从一种状态转移而来
因为是体积恰好是j,所以初始化时
memset(f,-0x3f,sizeof f)
f[0][0]=1;
memset(g,0,sizeof g)
g[0][0]=1;
再对空间复杂度进行优化
因为求得的是在每个体积的最大价值,不同的体积可能有相同的最大价值,
最后需要将所有有最大价值不同体积方案数累加求和
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N];
int g[N];
int main(){
int n,m;
cin>>n>>m;
memset(f,-0x3f,sizeof f);//求体积恰好等于j的最大价值
f[0]=0;
g[0]=1;//求体积恰好等于j的最大方案数
for(int i=0;i<n;i++){
int v,w;
scanf("%d%d",&v,&w);
for(int j=m;j>=v;j--){
int cnt;
if(f[j]<f[j-v]+w) cnt=g[j-v];
else if(f[j]==f[j-v]+w) cnt=g[j-v]+g[j];
else cnt=g[j];
g[j]=cnt%mod;
f[j]=max(f[j],f[j-v]+w);
}
}
int res=0;
for(int i=0;i<=m;i++) res=max(res,f[i]);//找出最大价值
int cnt=0;
for(int i=0;i<=m;i++) //找出所有体积不同的最大价值,每个体积有不同的方案数,累加求和
if(f[i]==res) cnt=(cnt+g[i])%mod;
cout<<cnt<<endl;
return 0;
}
完全背包问题求最优选法的方案数
从上面的几个例子我们也可以求出完全背包问题最大价值时的方案数
没有例题
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int f[N];
int g[N];
int main(){
int n,m;
cin>>n>>m;
memset(f,-0x3f,sizeof f);//求体积恰好等于j的最大价值
f[0]=0;
g[0]=1;//求体积恰好等于j的最大方案数
for(int i=0;i<n;i++){
int v,w;
scanf("%d%d",&v,&w);
for(int j=v;j<=m;j++){//改动在这里
int cnt;
if(f[j]<f[j-v]+w) cnt=g[j-v];
else if(f[j]==f[j-v]+w) cnt=g[j-v]+g[j];
else cnt=g[j];
g[j]=cnt%mod;
f[j]=max(f[j],f[j-v]+w);
}
}
int res=0;
for(int i=0;i<=m;i++) res=max(res,f[i]);//找出最大价值
int cnt=0;
for(int i=0;i<=m;i++) //找出所有体积不同的最大价值,每个体积有不同的方案数,累加求和
if(f[i]==res) cnt=(cnt+g[i])%mod;
cout<<cnt<<endl;
return 0;
}
应该是对的
01背包问题求具体方案
原题链接:AcWing 12. 背包问题求具体方案

01背包求具体方案只需要回溯输出结果就行
因为我们可以知道当前这一状态是从哪一个状态转移而来
因为题目要求字典序最小,所以可以反着算,正着回溯输出即可
代码如下:
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1010;
int f[N][N];
int v[N],w[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d%d",&v[i],&w[i]);
for(int i=n;i>=1;i--)
for(int j=0;j<=m;j++){
f[i][j]=f[i+1][j];
if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
}
for(int i=1,j=m;i<=n;i++)
if(j>=v[i] && f[i][j]==f[i+1][j-v[i]]+w[i]){
cout<<i<<" ";
j-=v[i];
}
return 0;
}