前言

想要精通算法和SQL的成长之路 - 系列导航

一. 接雨水

原题链接

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

在这里插入图片描述
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

题目分析：首先我们从图中想一下，积水的条件是什么？对于每一块的积水区域 ，一定是最右侧的柱子高度 >= 最左侧的柱子高度。 同时对于任何一块积水处，一定有三种元素构成：

右墙。
低洼处（中间部位）
左墙。

这三个元素放到一条直线上，当坐标或者索引来看，他就对应了三个索引。那么这种情况下，对于具有一定的高度排序要求的，我们使用单调栈来解决这个问题。思路如下：

首先，我们需要计算积水的时候，希望当前找到的柱子肯定是前面找的任何柱子要高。那么我们就可以使用单调递减栈。
只有更低的柱子能够入栈，毕竟单调递减嘛。然后重点来了。当遇到高的柱子了那怎么办？
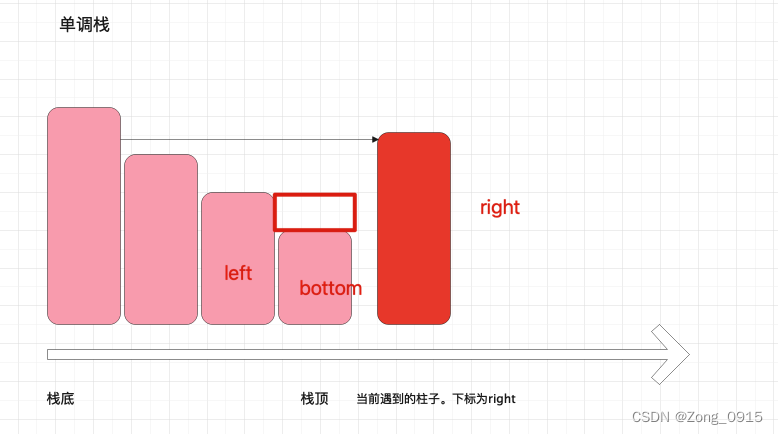
假设当前遇到的柱子索引是right。如图：

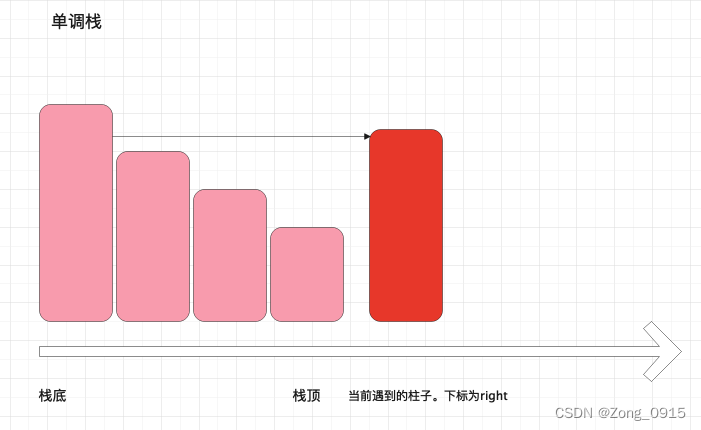
这个时候，就可以开始计算积水处了。我们需要遍历栈内元素。此时我们可以拿到三个坐标（彼此相邻）：

当前遇到的柱子（右墙）：right。对应高度就是height[right]。
低洼柱子：int bottom = stack.pop()（顺便把他弹出）。对应高度就是height[bottom]。
左墙：int left = stack.peek()。只是读，并为弹出哦。对应高度就是height[left]。

那么这相邻的三个柱子（实际上可能不相邻，但是计算起来的效果是等价的），他们造成的积水区域面积如图：红色框框部分。
在这里插入图片描述

长：right-left-1。
高：Math.min(rightHeight,leftHeight) - bottomHeight。
面积就是长乘高喽。

那这是和我们就把计算结果累加到总和上。进入下一次栈元素的遍历。遍历条件：当前柱子高度比栈顶柱子高。那么计算方式和上述一致。
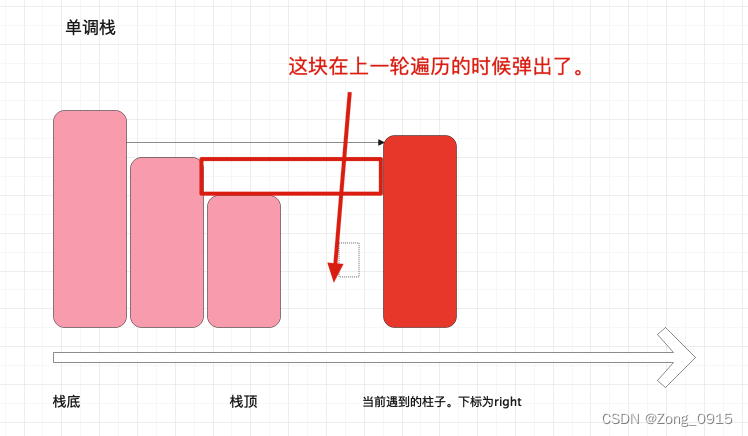
在这里插入图片描述
当栈顶元素高于当前遇到的柱子，那就退出循环，把当前柱子丢到栈里即可。

那么代码编写起来就容易啦：

public int trap(int[] height) {
    // 雨水总和
    int count = 0;
    // 单调栈，递减
    LinkedList<Integer> stack = new LinkedList<>();
    // 当前遍历的下标记为right
    for (int right = 0; right < height.length; right++) {
        // 当遇到的柱子高度 > 栈顶元素的时候，可以开始计算积水了。需要拿到低洼、左墙、右墙
        while (!stack.isEmpty() && height[stack.peek()] < height[right]) {
            Integer bottom = stack.pop();// 低洼下标
            // 特殊情况，如果没有左墙了就没必要循环了，因为构建不成积水
            if (stack.isEmpty()) {
                break;
            }

            Integer left = stack.peek();// 左墙下标
            int leftH = height[left];// 左墙高度
            int bottomH = height[bottom];// 低洼高度
            int rightH = height[right];// 右墙高度
            // 长 * 高 计算积水
            count += (right - left - 1) * (Math.min(leftH, rightH) - bottomH);
        }
        // 入栈，上边的while循环保证了这里入栈后的元素总是单调递减的。因为遇到高的，把比他小的全部给出栈了。
        stack.push(right);
    }
    return count;
}