经验风险
模型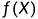
关于所有训练集上的平均损失称为经验风险或经验损失.
公式如下:
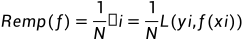
至此, 我们通过计算单点误差损失的平均值来衡量(刻画)模型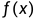
对训练集拟合的好坏, 但是我们如何衡量模型对未知数据的拟合能力呢, 也就是如何衡量模型在全体数据集上的性能, 因此我们引入概率论中两个随机变量的期望.
期望
期望和方差是随机变量两个最重要特征,随机变量的期望反应随机变量可能取值的平均水平, 而方差反映随机变量取之偏离与均值的平均程度.
数学期望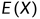
完全由随机变量
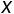的概率分布所确定, 若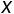服从某一分布, 也称
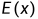)是这一分布的数学期望.
数学期望的意义
根据大数定律, 这个数字的意义是指随着重复次数接近无穷大时, 数值的算数平均值几乎肯定收敛于数学期望值, 也就是说数学期望值可以用于预测一个随机事件的平均预期情况.
平均值与期望
平均值和期望实际上是两个不同的概念, 很多人在实际使用时不会太在意他们的区别, 会导致后面的一些概念不清楚. 首先, 平均值属于数理统计的范畴, 而期望属于概率论的范畴.
期望风险
模型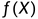
关于
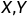的联合分布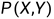
的平均意义下的损失成为风险函数或者期望损失, 损失函数和期望风险的关系: 期望风险是损失函数的期望值
损失函数的期望称为期望风险:
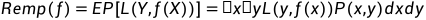
(连续变量求积分, 离散变量求和)
期望风险衡量的是模型在全体数据集上的性能.
两者之间的关系
总结经验风险和期望风险之间的关系:
- 经验风险是局部的, 基于训练集中所有样本点损失函数最小化, 经验风险是局部最优, 是现实可求的.
- 期望风险是全局的, 基于所有样本点损失函数最小化. 期望风险是全局最优, 是理想化的不可求的.
结构风险
实际上, 只考虑经验风险的话, 会出现过拟合的情况, 即模型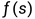
对于训练集中的所有样本点都有非常好的预测能力, 但是对于非训练集中的样本数据, 模型的预测能力缺非常差.
因此引入结构风险来对经验风险和期望风险的折中, 即在经验风险函数后面一个正则化项(惩罚项), 用来表示模型的复杂度.
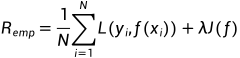
经验风险越小, 模型决策函数越复杂, 其包含的参数就越多, 当经验风险函数小到一定程度就出现了过拟合现象. 模型决策函数的复杂程度是过拟合的必要条件, 为了防止过拟合现象, 我们可以通过惩罚项来降低模型决策函数的复杂度.
