1.概念

二叉搜索树又称二叉排序树.利用中序遍历它就是一个有顺序的一组数.

2.性质

1.若它的左子树不为空,则左子树上所有节点的值都小于根节点的值

2.若它的右子树不为空,则右子树上所有节点的值都大于根节点的值

3.它的左右子树也分别为二叉搜索树

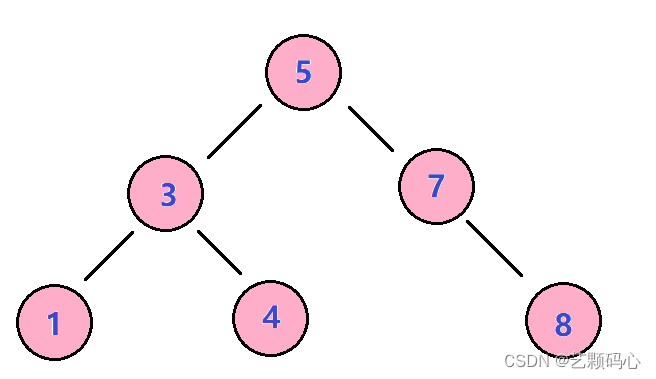
3.二叉搜索树的操作

1.查找

根据搜索树的性质来进行查找操作.

/**
     * 查找
     * @param root
     * @param val
     */
    public TreeNode find(TreeNode root, int val) throws FindException{
        if (root == null) {
            throw new FindException("root 为空");
        }
        while (root != null) {
            if (root.val == val) {
                return root;
            } else if (root.val < val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        return null;
    }

2.插入

每次插入进去的值都在叶子节点.

如果插入的是相同的数那么直接return. (在搜索树中插入相同的数没有意义)

/**
     * 插入
     * @param root
     * @param val
     * @return
     */
    public TreeNode insert(TreeNode root, int val) {
        if (root == null) {
            root = new TreeNode(val);
            return root;
        }
        TreeNode cur = root;
        TreeNode parent = null;
        while (cur != null) {
            parent = cur;
            if (cur.val < val) {
                cur = cur.right;
            } else {
                cur = cur.left;
            }
        }
        if (parent.val < val) {
            parent.right = new TreeNode(val);
        } else {
            parent.left = new TreeNode(val);
        }
        return root;
    }

3.删除(难点)

对于删除我们要去判断3种情况 : 假设要删除的节点是cur

一 . cur.left == null 在这个前提下还有三种情况:

1 . cur 是 root , root = cur.right;

2 . cur不是root, cur是parent.left ; parent.left = cur.right;

3 . cur不是root, cur是parent.right; parent.right = cur.right;

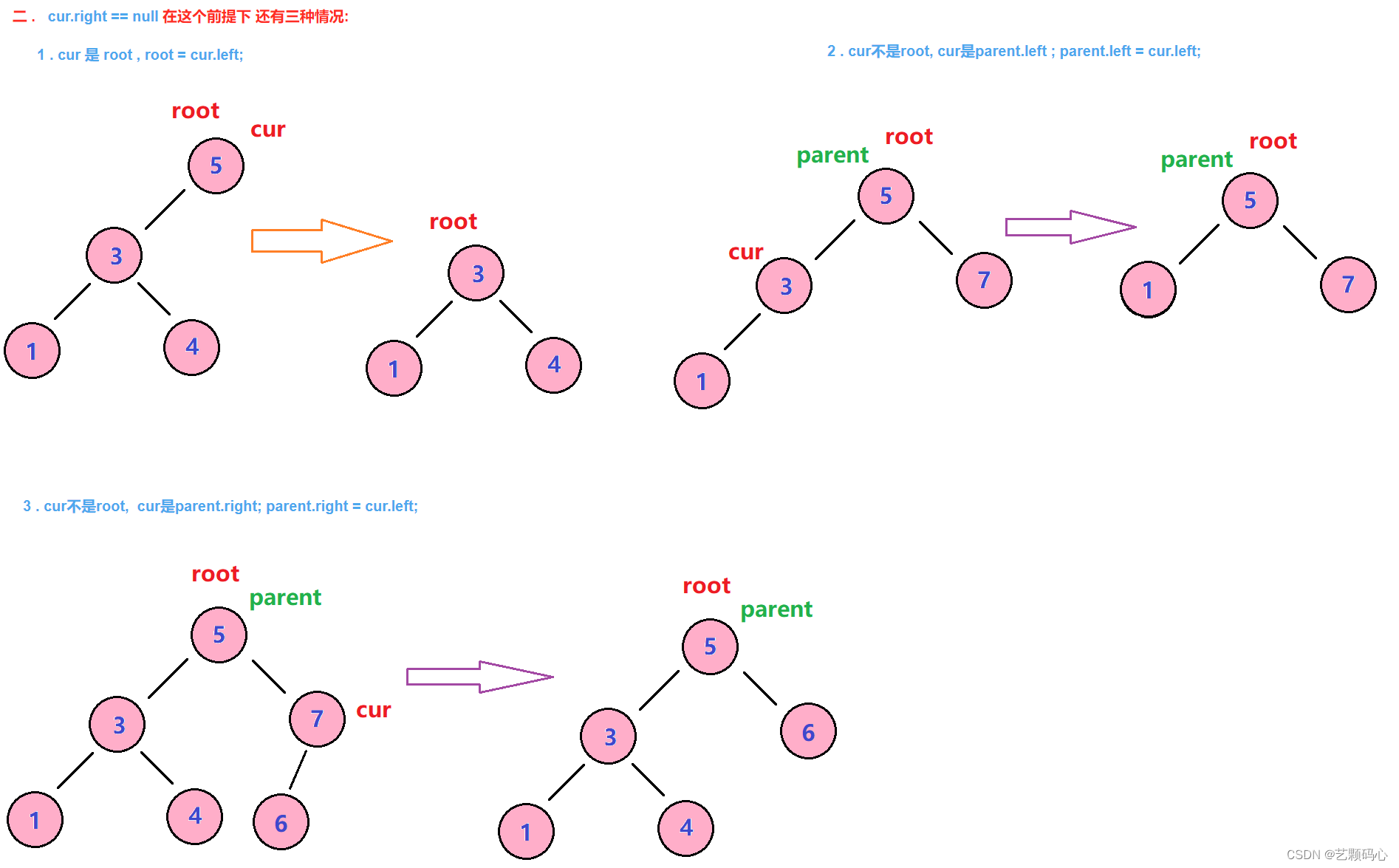
二 . cur.right == null 在这个前提下还有三种情况:

1 . cur 是 root , root = cur.left;

2 . cur不是root, cur是parent.left ; parent.left = cur.left;

3 . cur不是root, cur是parent.right; parent.right = cur.left;

三 (重). cur 的左右都不为空 :

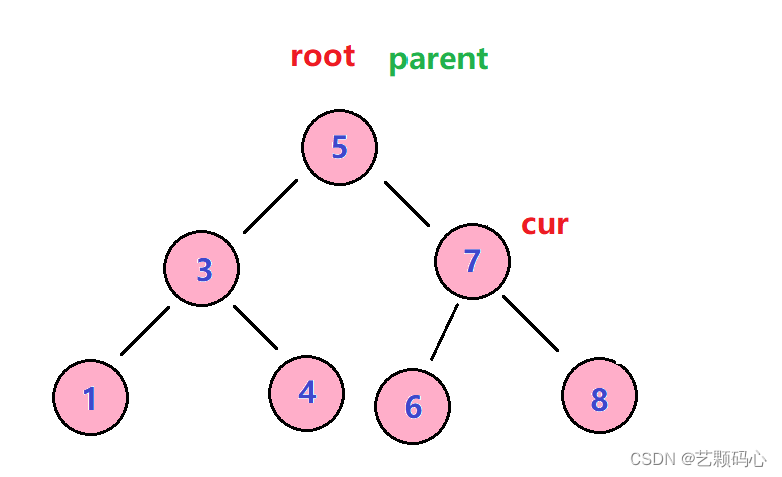
思路 : 假设要被删除的是cur , 我们去找到cur右树中最小的那个节点 . 把它的val值跟cur.val交换.

交换之后我们的任务就是去删除交换后的那个节点(之前右树中最小的值).

但是这样做的话还有一个问题 : 在我们去删被交换后的那个节点时,它的左子树肯定是空的.

比如是这样 :

第一种情况 :

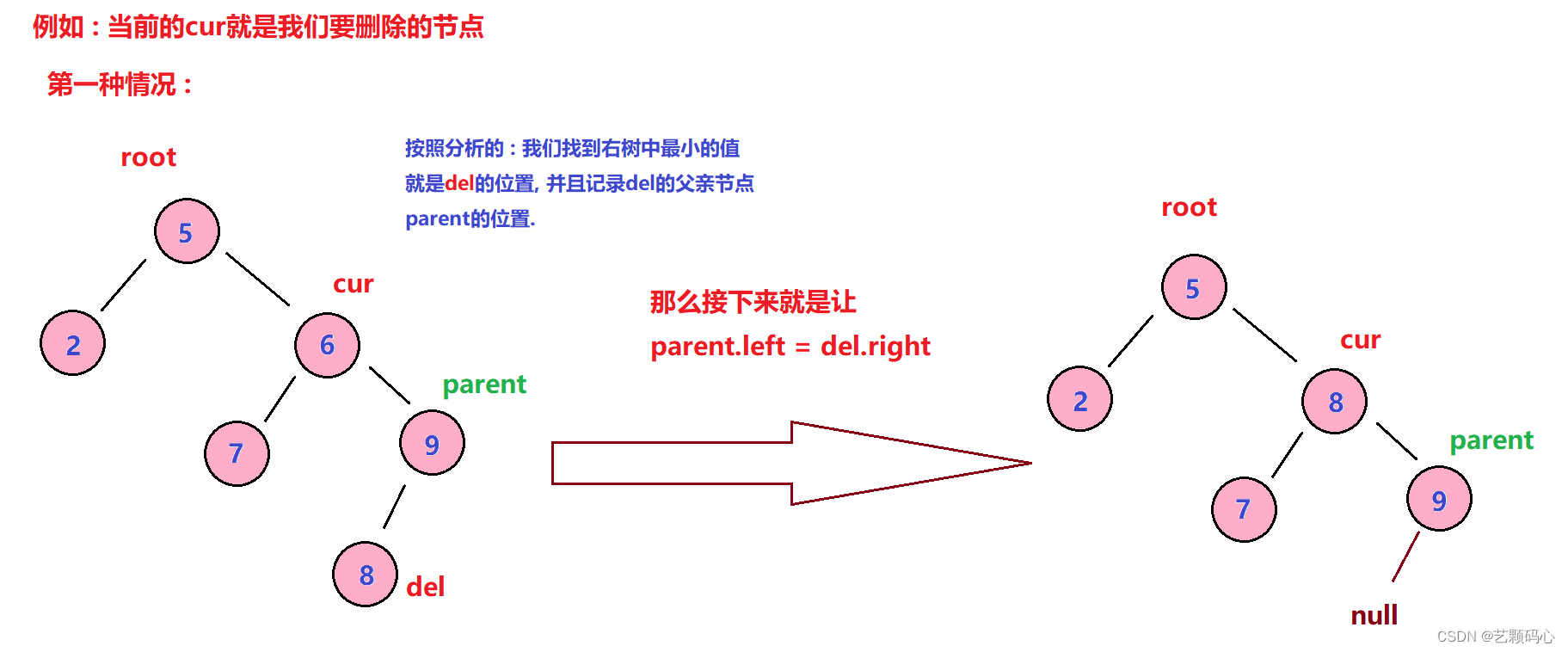
第二种情况 :

结合以上两种情况 : 我们就要去判断parent.left == del 还是 parent.right = del

代码实现 :

public class BinarySearchTree {
    static class TreeNode {
        public int val;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    /**
     * 查找
     * @param root
     * @param val
     */
    public TreeNode find(TreeNode root, int val) throws FindException{
        if (root == null) {
            throw new FindException("root 为空");
        }
        while (root != null) {
            if (root.val == val) {
                return root;
            } else if (root.val < val) {
                root = root.right;
            } else {
                root = root.left;
            }
        }
        return null;
    }

    /**
     * 插入
     * @param root
     * @param val
     * @return
     */
    public TreeNode insert(TreeNode root, int val) {
        if (root == null) {
            root = new TreeNode(val);
            return root;
        }
        TreeNode cur = root;
        TreeNode parent = null;
        while (cur != null) {
            parent = cur;
            if (cur.val < val) {
                cur = cur.right;
            } else {
                cur = cur.left;
            }
        }
        if (parent.val < val) {
            parent.right = new TreeNode(val);
        } else {
            parent.left = new TreeNode(val);
        }
        return root;
    }
    //中序遍历
    public void inorder(TreeNode root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        System.out.print(root.val + " ");
        inorder(root.right);
    }

    /**
     * 删除
     * @param root
     * @param val
     */
    public void remove(TreeNode root, int val) {
        TreeNode cur = root;
        if (cur == null) {
            throw new RootNullException("root 为空");
        }
        TreeNode parent = null;
        while (cur != null) {
            if (cur.val == val) {
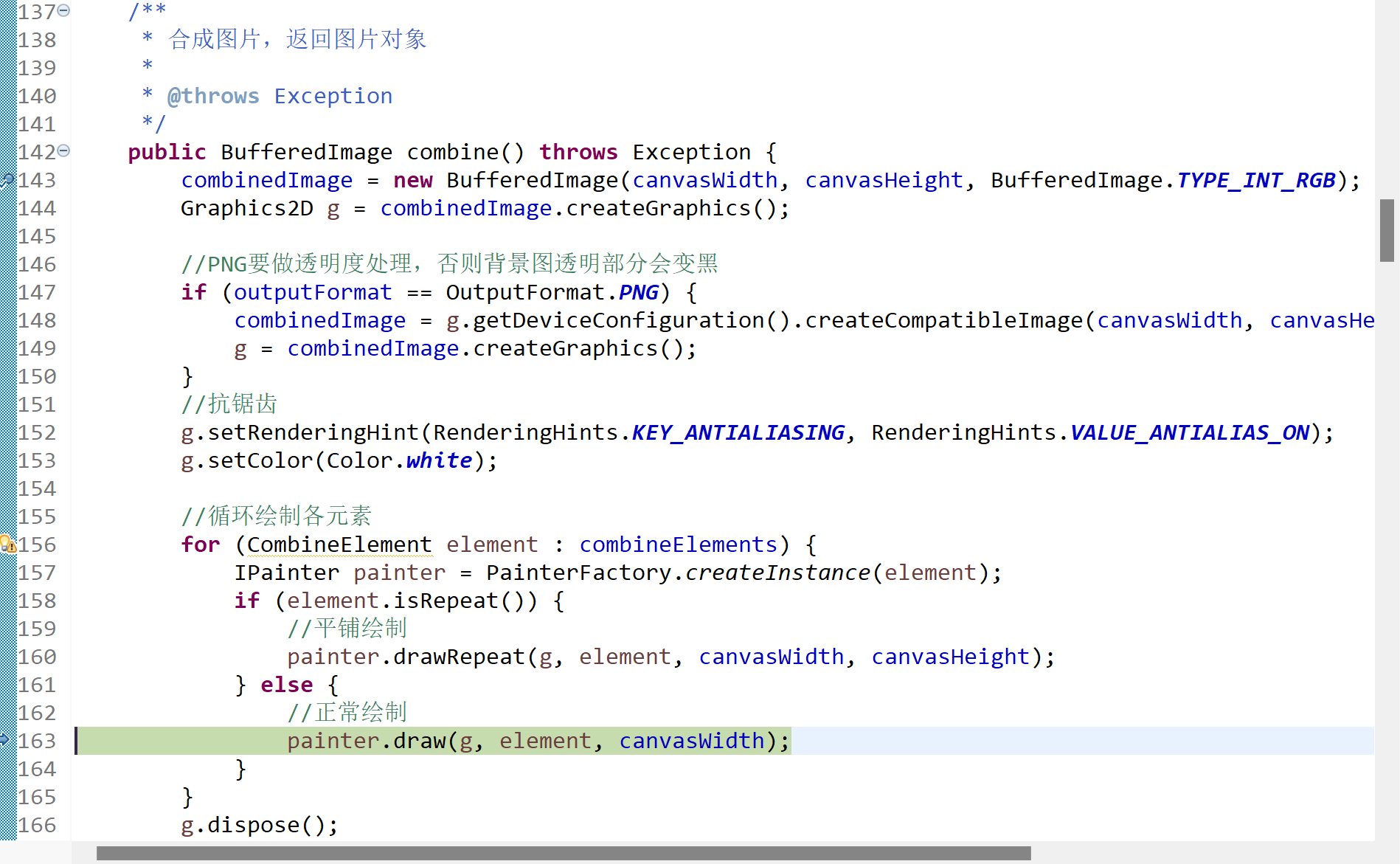
                del(cur,parent,root);
                break;
            } else if (cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else {
                parent = cur;
                cur = cur.left;
            }
        }
    }
    //删除cur节点
    public void del(TreeNode cur, TreeNode parent, TreeNode root) {
        if (cur.left == null) {
            if (cur == root) {
                root = root.right;
            } else if (parent.right == cur) {
                parent.right = cur.right;
            } else {
                parent.left = cur.right;
            }
        } else if (cur.right == null) {
            if (cur == root) {
                root = root.left;
            } else if (parent.right == cur) {
                parent.right = cur.left;
            } else {
                parent.left = cur.left;
            }
        } else {
            //程序到这 就是cur的左右都不为空
            TreeNode del = cur.right;
            parent = cur;
            while (del.left != null) {
                parent = del;
                del = del.left;
            }
            cur.val = del.val;
            if (parent.right == del) {
                parent.right = del.right;
            } else {
                parent.left = del.right;
            }
        }
    }
}

以上就是关于搜索树的一些基本操作.

有任何问题可以私信我!

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/335524.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！