【运筹优化】Python 实现标签算法求解 ESPPRC 问题

news2024/11/29 12:51:24

文章目录

  • 一、标签算法介绍
  • 二、SPPRC 问题
  • 三、ESPPRC 问题
  • 四、Python 实现标签算法求解 ESPPRC 问题
    • 4.1 Solomn 数据集
    • 4.2 完整代码
      • 4.2.1 Functions.py
      • 4.2.2 LabelAlgo.py
      • 4.2.3 Main.py
    • 4.3 结果展示
      • 4.3.1 测试案例：c101.txt
      • 4.3.2 测试案例：r101.txt

一、标签算法介绍

标签算法(Labeling algorithms)是解决最短路径问题的一种重要方法，也是绝大多数最短路径算法的核心部分。

按照不同的标识结点处理策略，标签算法又可分为标签设定(Label Setting，简称LS)和标签校正(Label Correcting，简称LC)两大体系。

有关最短路径问题的两个经典算法，Dijkstra算法和Bellman-Ford算法，分别属于LS和LC。

LS算法通过迭代过程对label进行逐步设定，每次迭代均选择候选结点集中标号最小者退出候选结点集，并将该结点标签从临时标签转变久为永久标号。这是一种基于贪心策略的最短路径算法，每一次转化为永久标号的label都代表到当前结点的最短路径，考虑的是“当前最优”。

LC算法在每次迭代时并不一定将任何结点标签从临时标号转变为永久标签，只是对临时标签进行一次修正，所有结点标签仍然为临时标签；只有在所有迭代终止时，所有结点标号同时转变为永久标签。LC算法考虑的是“最终最优”，最短路径需要等待多次迭代直到整个算法运行结束才能被确定。

本博客实现的是标签校正算法。

二、SPPRC 问题

带资源约束的最短路径问题 (shortest path problem with resource constraints，SPPRC) 是一个众所周知的NP-Hard问题。除了作为网络 问题直接应用外，SPPRC还用作列生成解决方案方法的基础，用于解决车辆路径规划问题和人员排班问题等。
考虑一个有向图 G = ( N , A ) , N = { v 1 , v 2 , … , v i , … , v n } G=(N, A), N=\left\{v_1, v_2, \ldots, v_i, \ldots, v_n\right\} G=(N,A),N={v1​,v2​,…,vi​,…,vn​} 表示节点的集合，并且 A = { ( i , j ) ∣ v i ∈ N , v j ∈ N , i ≠ j } A=\left\{(i, j) \mid v_i \in N, v_j \in N, i \neq j\right\} A={(i,j)∣vi​∈N,vj​∈N,i=j} 表示弧的 集合。对于每一段弧 ( i , j ) ∈ A (\mathrm{i}, \mathrm{j}) \in \mathrm{A} (i,j)∈A 都有一个非负的权重(vrptw问题中可能为负，需要作特殊处理)， c i j \mathrm{c}_{\mathrm{ij}} cij​ 和 t i j \mathrm{t}_{\mathrm{ij}} tij​ ，表示通过这段弧的成本和资源消 耗。

SPPRC问题包括找到从起始节点 v s ∈ N \mathrm{v}_{\mathrm{s}} \in \mathrm{N} vs​∈N 到结束节点 v t ∈ N \mathrm{v}_{\mathrm{t}} \in \mathrm{N} vt​∈N 的一条路径 P P P ，使该路径的总成本最小化，但不超过最大资源消耗 T T T 。 即使只存在一种资源，SPPRC也是一个NP-Hard。

三、ESPPRC 问题

带资源约束的基本最短路径问题(Elementary shortest path problem with resource constraints)，以下简称ESPPRC。

从名字上看，SPPRC是把"elementary"约束给松弛了的。Elementary意为：每一个点只能被访问一次。松弛了一个约束，大体上会使得原问题简单一些。

四、Python 实现标签算法求解 ESPPRC 问题

4.1 Solomn 数据集

Solomn 数据集下载地址

4.2 完整代码

4.2.1 Functions.py

# -*- coding: utf-8 -*-#
# Author: WSKH
# Blog: wskh0929.blog.csdn.net
# Time: 2023/2/9 13:04
# Description:
import math
import re
import numpy as np
from matplotlib import pyplot as plt


class Data:
    customerNum = 0
    nodeNum = 0
    vehicleNum = 0
    capacity = 0
    corX = []
    corY = []
    demand = []
    serviceTime = []
    readyTime = []
    dueTime = []
    distanceMatrix = [[]]


def readData(path, customerNum):
    data = Data()
    data.customerNum = customerNum
    if customerNum is not None:
        data.nodeNum = customerNum + 2
    with open(path, 'r') as f:
        lines = f.readlines()
        count = 0
        for line in lines:
            count += 1
            if count == 5:
                line = line[:-1]
                s = re.split(r" +", line)
                data.vehicleNum = int(s[1])
                data.capacity = float(s[2])
            elif count >= 10 and (customerNum is None or count <= 10 + customerNum):
                line = line[:-1]
                s = re.split(r" +", line)
                data.corX.append(float(s[2]))
                data.corY.append(float(s[3]))
                data.demand.append(float(s[4]))
                data.readyTime.append(float(s[5]))
                data.dueTime.append(float(s[6]))
                data.serviceTime.append(float(s[7]))
    data.nodeNum = len(data.corX)
    data.customerNum = data.nodeNum - 1
    # 计算距离矩阵
    data.distanceMatrix = np.zeros((data.nodeNum, data.nodeNum))
    for i in range(data.nodeNum):
        for j in range(i + 1, data.nodeNum):
            distance = math.sqrt((data.corX[i] - data.corX[j]) ** 2 + (data.corY[i] - data.corY[j]) ** 2)
            data.distanceMatrix[i][j] = data.distanceMatrix[j][i] = distance
    return data


def calc_path_distance(path, data):
    dis = 0
    for i in range(len(path) - 1):
        dis += data.distanceMatrix[path[i]][path[i + 1]]
    return dis


def calc_path_load(path, data):
    load = 0
    for i in range(len(path)):
        load += data.demand[path[i]]
    return load


def check_time_window(path, data):
    cur_time = 0
    for i in range(len(path) - 1):
        cur_time += data.distanceMatrix[path[i]][path[i + 1]]
        if cur_time < data.readyTime[path[i + 1]] or cur_time > data.dueTime[path[i + 1]]:
            return False
    return True


def plot_path(title, path, data):
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title(title)
    plt.scatter(data.corX[0], data.corY[0], c='red', alpha=1, marker='v', linewidths=3, label='org')  # 起点
    plt.scatter(data.corX[1:-1], data.corY[1:-1], c='black', alpha=1, marker='o', linewidths=3,
                label='mid')  # 中间站点
    plt.scatter(data.corX[-1], data.corY[-1], c='blue', alpha=1, marker='s', linewidths=3,
                label='des')  # 终点
    for i in range(len(path) - 1):
        a = int(path[i])
        b = int(path[i + 1])
        x = [data.corX[a], data.corX[b]]
        y = [data.corY[a], data.corY[b]]
        plt.plot(x, y, 'k', linewidth=1)
    plt.grid(False)
    plt.legend(loc='best')
    plt.show()

4.2.2 LabelAlgo.py

注意：is_dominate函数我没有写，我一开始也想了一个优超准则的，但是经过实验会导致求出来的解不一定是最优的，所以我注释掉了，如果你知道优超准则怎么写，欢迎在评论区留言！（正确的优超准则可以在确保结果的最优性的同时，减少不必要的搜索，提高求解效率。当然不写优超准则也没事，只是求解效率会相对低一些）

# -*- coding: utf-8 -*-#
# Author: WSKH
# Blog: wskh0929.blog.csdn.net
# Time: 2023/2/9 13:02
# Description:

wei = 15


class Label:
    path = []
    travel_time = 0
    distance = 0
    load = 0

    def __init__(self, node_num):
        self.node_num = node_num
        l = (node_num // wei) + 1
        self.node_set = [0 for _ in range(l)]

    def append(self, node):
        i = node // wei
        j = node % wei
        self.node_set[i] = self.node_set[i] | (1 << j)
        self.path.append(node)

    def have_node(self, node):
        i = node // wei
        j = node % wei
        return self.node_set[i] & (1 << j) != 0


def copy_label(label):
    c_label = Label(label.node_num)
    c_label.path = label.path.copy()
    c_label.travel_time = label.travel_time
    c_label.distance = label.distance
    c_label.load = label.load
    c_label.node_set = label.node_set.copy()
    return c_label


def is_dominate(Q, extended_label, t, load, d):
    # for label in Q:
    #     if label.path[-1] == extended_label.path[
    #         -1] and label.travel_time < t and label.distance < d and label.load < load:
    #         b = True
    #         for i in range(len(label.node_set)):
    #             if label.node_set[i] | extended_label.node_set[i] != extended_label.node_set[i]:
    #                 # 说明 label.path 不是 extended_path 的子集
    #                 b = False
    #                 break
    #         if b is True:
    #             # 说明 label.path 是 extended_path 的子集，extended_path 要被 dominate
    #             return True
    return False


# labeling algorithm
def Labeling_SPPRC(data, org, des):
    # initial opt_labels
    opt_labels = []
    # initial Q
    Q = []
    # create initial label
    label = Label(data.nodeNum)
    label.append(org)
    Q.append(label)
    # start search
    while len(Q) > 0:
        current_label = Q.pop()
        # print(current_label.path)
        if current_label.path[-1] == des:
            if len(opt_labels) == 0:
                opt_labels = [current_label]
            else:
                if abs(opt_labels[0].distance - current_label.distance) < 0.000001:
                    opt_labels.append(current_label)
                elif opt_labels[0].distance > current_label.distance:
                    opt_labels = [current_label]
            continue
        # extend the current label
        last_node = current_label.path[-1]
        for next_node in range(data.nodeNum):
            # current_label.have_node(next_node) is False
            # next_node not in current_label.path
            if next_node not in current_label.path:
                extended_label = copy_label(current_label)
                # check the feasibility
                arrive_time = current_label.travel_time + data.distanceMatrix[last_node][next_node]
                load = extended_label.load + data.demand[next_node]
                if load <= data.capacity and data.readyTime[next_node] <= arrive_time <= data.dueTime[next_node]:
                    # dominate rule
                    extended_label.append(next_node)
                    d = extended_label.distance + data.distanceMatrix[last_node][next_node]
                    dominate = is_dominate(Q, extended_label, arrive_time, load, d)
                    if dominate is False:
                        extended_label.travel_time = arrive_time
                        extended_label.distance = d
                        extended_label.load = load
                        Q.append(extended_label)
                    else:
                        # print(extended_label.path)
                        pass
    # return
    return opt_labels

4.2.3 Main.py

# -*- coding: utf-8 -*-#
# Author: WSKH
# Blog: wskh0929.blog.csdn.net
# Time: 2023/2/9 13:03
# Description:
import time

from Functions import *
from LabelAlgo import *

if __name__ == '__main__':
    # 哪个数据集
    data_type = "c101"
    # 数据集路径
    data_path = f'../../data/solomn_data/{data_type}.txt'
    # 顾客个数设置（从上往下读取完 customerNum 个顾客为止，例如c101文件中有100个顾客点，
    # 但是跑100个顾客点太耗时了，设置这个数是为了只选取一部分顾客点进行计算，用来快速测试算法）
    # 如果想用完整的顾客点进行计算，设置为None即可
    customerNum = 20
    # 读取数据
    data = readData(data_path, customerNum)
    # 指定起点和终点
    org = 0
    des = data.nodeNum - 1
    # 输出相关数据
    print("-" * 20, "Problem Information", '-' * 20)
    print(f'Data Type: {data_type}')
    print(f'Node Num: {data.nodeNum}')
    print(f'Customer Num: {data.customerNum}')
    print(f'Vehicle Num: {data.vehicleNum}')
    print(f'Vehicle Capacity: {data.capacity}')
    # 开始求解
    start_time = time.time()
    opt_labels = Labeling_SPPRC(data, org, des)
    print("-" * 20, "Solved Completely", '-' * 20)
    if len(opt_labels) > 0:
        print(f"Solve Time: {time.time() - start_time} s")
        for i in range(len(opt_labels)):
            print(
                f'Optimal Solution {i + 1} : {opt_labels[i].path} , load: {opt_labels[i].load} , distance: {opt_labels[i].distance} , check_time_window: {check_time_window(opt_labels[i].path, data)}')
            plot_path(f'Optimal Solution {i + 1}', opt_labels[i].path, data)
    else:
        print("There is no solution to this question")

4.3 结果展示

4.3.1 测试案例：c101.txt

设置 customerNum = 20

-------------------- Problem Information --------------------
Data Type: c101
Node Num: 21
Customer Num: 20
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 0.0 s
Optimal Solution 1 : [0, 20] , load: 10.0 , distance: 10.0 , check_time_window: True

在这里插入图片描述

设置 customerNum = 35

-------------------- Problem Information --------------------
Data Type: c101
Node Num: 36
Customer Num: 35
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 0.06851029396057129 s
Optimal Solution 1 : [0, 20, 5, 32, 3, 33, 7, 25, 18, 27, 35] , load: 200.0 , distance: 289.7898204179148 , check_time_window: True

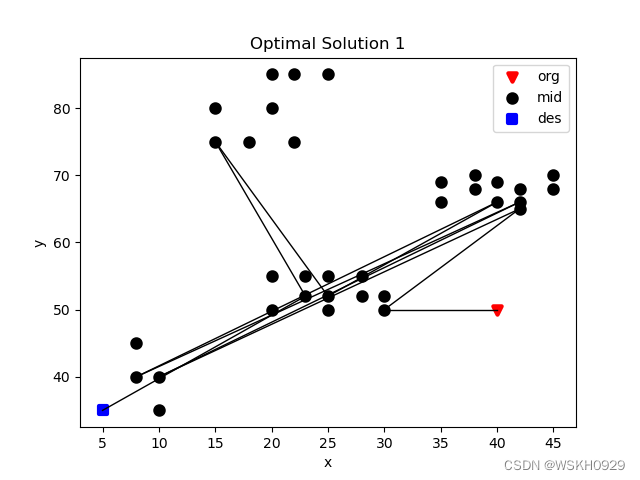
在这里插入图片描述

设置 customerNum = 55

-------------------- Problem Information --------------------
Data Type: c101
Node Num: 56
Customer Num: 55
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 28.623275756835938 s
Optimal Solution 1 : [0, 5, 32, 55] , load: 50.0 , distance: 96.34850796740938 , check_time_window: True

在这里插入图片描述

4.3.2 测试案例：r101.txt

设置 customerNum = 55

-------------------- Problem Information --------------------
Data Type: r101
Node Num: 56
Customer Num: 55
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 0.0375361442565918 s
Optimal Solution 1 : [0, 14, 2, 44, 16, 55] , load: 66.0 , distance: 136.55961482272318 , check_time_window: True

在这里插入图片描述

设置 customerNum = 75

-------------------- Problem Information --------------------
Data Type: r101
Node Num: 76
Customer Num: 75
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 0.47461438179016113 s
Optimal Solution 1 : [0, 14, 21, 75] , load: 49.0 , distance: 73.48725559064414 , check_time_window: True

在这里插入图片描述

设置 customerNum = 85

-------------------- Problem Information --------------------
Data Type: r101
Node Num: 86
Customer Num: 85
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 1.7239580154418945 s
Optimal Solution 1 : [0, 63, 69, 85] , load: 57.0 , distance: 91.74424577496413 , check_time_window: True

在这里插入图片描述

设置 customerNum = 100

-------------------- Problem Information --------------------
Data Type: r101
Node Num: 101
Customer Num: 100
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Completely --------------------
Solve Time: 32.46246600151062 s
Optimal Solution 1 : [0, 92, 27, 28, 69, 30, 79, 97, 74, 100] , load: 121.0 , distance: 185.00120247142092 , check_time_window: True

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/335377.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

2022年38女神节大促美妆、珠宝、母婴、保健电商数据回顾

2022年38女神节大促美妆、珠宝、母婴、保健电商数据回顾

近期&#xff0c;我们陆续接收到了品牌商家朋友们对于2022年女神节大促期间部分品类的数据需求&#xff0c;希望能对今年的大促活动有一个更宏观的认知、更精准的预测&#xff0c;从而拿到更好的数据效果。 为此&#xff0c;在距离大促开启一个月的备货阶段&#xff0c;鲸参谋决…
阅读更多...
ChatGPT真的像媒体宣传的那样“四平八稳”吗？

ChatGPT真的像媒体宣传的那样“四平八稳”吗？

最近ChatGPT非常的火爆&#xff0c;曝光度很高&#xff0c;很多官方媒体和个人的自媒体公众号都进行各种追逐。有些文案写的太好了&#xff0c;真的都要信了。其中有一篇“遨游四海&#xff0c;惊艳于某州”类似旅游宣传的文案。为了测试一下于是仿照他们的问话方式对ChatGPT进…
阅读更多...
【服务器数据恢复】服务器raid5故障导致lvm结构损坏的数据恢复案例

【服务器数据恢复】服务器raid5故障导致lvm结构损坏的数据恢复案例

服务器数据恢复环境&#xff1a; 服务器内搭建2组raid5磁盘阵列&#xff0c;每组raid5阵列包含4个磁盘&#xff0c;2组阵列都划分为lun并组为lvm结构&#xff0c;采用的ext3文件系统。 服务器故障&#xff1a; 一直raid5磁盘阵列中的一块硬盘由于未知故障离线&#xff0c;此时该…
阅读更多...
【4】深度学习之Pytorch——如何使用张量处理时间序列数据集（共享自行车数据集）

【4】深度学习之Pytorch——如何使用张量处理时间序列数据集（共享自行车数据集）

表格数据 表格中的每一行都独立于其他行&#xff0c;他们的顺序页没有任何关系。并且&#xff0c;没有提供有关行之前和行之后的列编码信息。 表格类型的数据是指通过表格的形式表示的数据&#xff0c;它以行和列的方式组织数据。表格中的每一行代表一个数据项&#xff0c;每…
阅读更多...
九龙证券|A股苏州板块迎来“200+”里程碑

九龙证券|A股苏州板块迎来“200+”里程碑

2月10日&#xff0c;跟着裕太微登陆科创板&#xff0c;A股“姑苏板块”正式迎来第201位成员。姑苏也成为继京、沪、深、杭之后&#xff0c;第5个具有A股上市公司总数超越200家的城市。 现在&#xff0c;姑苏不仅生长为位居全国前列的“制作之都”&#xff0c;更成为资本市场高地…
阅读更多...
通过对HashMap的源码分析解决部分关于HashMap的问题

通过对HashMap的源码分析解决部分关于HashMap的问题

HashMap第一次分配多大的空间我们查看resize&#xff08;)中的源码所以当我们没有传入默认容量的参数的时候&#xff0c;默认容量是16当传进一个20的初始参数时&#xff0c;数组的容量是多大所以当我们传入20的参数&#xff0c;这时创建的容量是32&#xff08;2^5&#xff09;对…
阅读更多...
电子采购一体化解决方案

电子采购一体化解决方案

企事业数字化转型专家&#xff0c;提供各类应用解决方案。您身边的赋能小助手&#xff01; 文章目录前言一、当下采购的痛点二、解决方案-供应商管理1.供应商管理三、解决方案-企业询价、供应商报价管理四、解决方案-采购订单五、送货、到货、订单管理总结前言 随着各类产业链…
阅读更多...
世界上最大的12个超大规模自建数据中心企业

世界上最大的12个超大规模自建数据中心企业

Hyperscalers 经常与托管服务提供商合作以满足需求并解决他们的需求。但随着它们变得越来越大&#xff0c;超大规模企业已经转向建立自己的数据中心。 规模是选择自建的关键决定因素&#xff0c;但其他变量也出现了&#xff0c;包括减少供应商、定制和控制设计以及获取可再生能…
阅读更多...
Linux搭建redis集群6.x版本【超简单】

Linux搭建redis集群6.x版本【超简单】

Linux搭建redis集群6.x版本【超简单】&#xff1a;&#xff1a;&#xff1a;&#xff1a;本文主要展示如何在一台服务器上搭建集群&#xff0c;核心思想就是复制实例&#xff0c;修改启动端口&#xff0c;实际上跟在几台服务器的操作都是一样的。一.安装redis wget http://dow…
阅读更多...
docker入门基础(安装docker部署应用)

docker入门基础(安装docker部署应用)

docker基础容器技术发展 文章目录docker基础容器技术发展1.什么是容器&#xff1f;2.容器和虚拟化的区别3.docker官网文档地址4.docker基本组成5.安装docker5.1.调整系统环境5.2.准备工作5.3.下载所需的插件5.4.下载镜像仓库5.5.安装docker5.6.启动docker5.7.hello-world 命令5…
阅读更多...
DHCP安全及防范

DHCP安全及防范

DHCP安全及防范DHCP面临的威胁DHCP饿死攻击仿冒DHCP Server攻击DHCP中间人攻击DHCP Snooping技术的出现DHCP Snooping防饿死攻击DHCP Snooping防止仿冒DHCP Server攻击DHCP Snooping防止中间人攻击DHCP Snooping防止仿冒DHCP报文攻击DHCP面临的威胁 网络攻击无处不在&#xff…
阅读更多...
【JavaSE】深入HashMap

【JavaSE】深入HashMap

文章目录1. HashMap概述2. 哈希冲突3. 树化与退化3.1 树化的意义3.2 树的退化4. 二次哈希5. put方法源码分析6. key的设计7. 并发问题参考 如何防止因哈希碰撞引起的DoS攻击_hashmap dos攻击_双子孤狼的博客-CSDN博客 为什么 HashMap 要用 h^(h &#xff1e;&#xff1e;&#…
阅读更多...
动态代理是基于什么原理？

动态代理是基于什么原理？

第6讲 | 动态代理是基于什么原理&#xff1f; 编程语言通常有各种不同的分类角度&#xff0c;动态类型和静态类型就是其中一种分类角度&#xff0c;简单区分就是语言类型信息是在运行时检查&#xff0c;还是编译期检查。 与其近似的还有一个对比&#xff0c;就是所谓强类型和弱…
阅读更多...
ChatGPT is at capacity right now错误解决，ChatGPT问题汇总

ChatGPT is at capacity right now错误解决，ChatGPT问题汇总

我是老鱼&#xff0c;一名致力于在技术道路上的终身学习者、实践者、分享者&#xff01; 最近ChatGPT大火&#xff01;微软退出首款ChatGPT搜索引擎&#xff0c;阿里等国内巨头也纷纷爆出自家产品&#xff0c;一夜之间&#xff0c;全球最大的科技公司仿佛都回到了自己年轻时的…
阅读更多...
CUDA By Example(八)——流

CUDA By Example(八)——流

文章目录页锁定主机内存可分页内存函数页锁定内存函数CUDA流使用单个CUDA流使用多个CUDA流GPU的工作调度机制高效地使用多个CUDA流遇到的问题(未解决)页锁定主机内存 在之前的各个示例中&#xff0c;都是通过 cudaMalloc() 在GPU上分配内存&#xff0c;以及通过标准的C库函数 …
阅读更多...
【数据结构】栈(stack)

【数据结构】栈(stack)

写在前面本篇文章开始讲解栈的有关知识&#xff0c;其实把顺序表和链表学好&#xff0c;那么这一章便不在话下&#xff0c;栈实际上就是顺序表或链表的一些特殊情况。用顺序表实现的栈叫做顺序栈用链表实现的栈叫做链栈文章的内容分为几个部分&#xff0c;希望读者能快速了解文…
阅读更多...
经过去年的一遍技术洗礼，《最新的Android 核心知识点》出炉了~

经过去年的一遍技术洗礼，《最新的Android 核心知识点》出炉了~

金三银四即将来临&#xff0c;相信很多人的心已经在开始蠢蠢欲动准备新年过后跳槽换一个好点的坑位了&#xff0c;披荆斩棘&#xff0c;斩关过将“杀掉”一众竞争对手 &#xff0c;最后成功靠着跳槽涨薪走上人生巅峰&#xff01; 理想很丰满现实慌得一批&#xff0c;大批大批的…
阅读更多...
Docker进阶 - 6. docker network 网络模式之bridge

Docker进阶 - 6. docker network 网络模式之bridge

1. bridge概述 Docker 服务默认会创建一个 docker0 网桥(其上有一个 docker0 内部接口)&#xff0c;该桥接网络的名称为docker0&#xff0c;它在内核层连通了其他的物理或虚拟网卡&#xff0c;这就将所有容器和本地主机都放到同一个物理网络。Docker 默认指定了docker0接口的…
阅读更多...
ucore的字符输出

ucore的字符输出

ucore的字符输出有cga,lpt,和串口。qemu模拟出来显示器连接到cga中。 cga cga的介绍网站&#xff1a;https://en.wikipedia.org/wiki/Color_Graphics_Adapter cga是显示卡&#xff0c;内部有个叫6845的芯片。cga卡把屏幕划分成一个一个单元格&#xff0c;每个单元格显示一个a…
阅读更多...
“数字孪生”：为什么要仿真嵌入式系统？

“数字孪生”：为什么要仿真嵌入式系统？

​01.仿真是什么&#xff1f; 仿真的概念非常广泛&#xff0c;但归根结底都是使用可控的手段来模仿真实的情况&#xff0c;通常应用于现实世界中实施难度大甚至是无法实践的事物。 众所周知&#xff0c;嵌入式系统通常是形式多样的、面向特定应用的软硬件综合体&#xff0c;无…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023