文章目录
前言
一、顺序表的概念
二、顺序表功能接口概览
三、顺序表基本功能的实现
四、四大功能
1、增加数据
1.1 头插法:
1.2 尾插法
1.3 指定下标插入
2、删除数据
2.1 头删
2.2 尾删
2.3 指定下标删除
2.4 删除首次出现的指定元素
3、查找数据
3.1 获取指定位置的元素
3.2 获取指定元素所在的位置
3.3 查找表中是否包含某个元素
4、修改数据
4.1 修改表中任意位置的元素
五、代码总结
MyArraysList.java
Test.java
总结
前言
今天我们将开始学习数据结构的第一个重点知识,顺序表的学习;顺序表是我们学习数据结构的第一个重点,一定要认真掌握,为后面其他的数据结构打下坚实的基础;
那就让我们进入到今天的课程当中吧!!!!!!!!!
一、顺序表的概念
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构;
一般情况下采用数组存储,在数组上完成数据的增删查改。
顺序表一般可以分为:
- 静态顺序表:使用定长数组存储元素。(本篇主要围绕静态顺序表展开)
- 动态顺序表:使用动态开辟的数组存储。
二、顺序表功能接口概览
本文将创建两个Java文件:MyArraysList.java用于顺序表的实现,Test.java用于顺序表的各个接口的测试
代码示例:
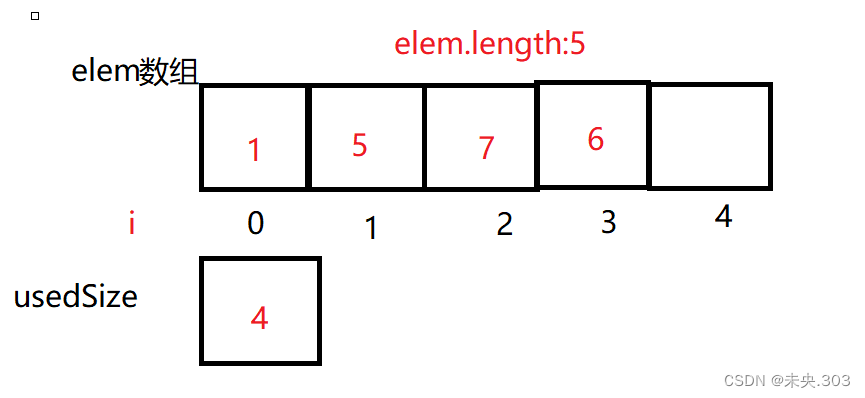
import java.util.Arrays; public class MyArraysList { private int[] elem; private int usedSize; // 默认值是0 private static final int DEFAULT_SIZE = 4; // 定义为常量,更加安全 // 初始化顺序表 public MyArraysList() { this.elem = new int[4]; } // 对顺序表进行扩容 public void expand() {} //判断当前顺序表是否为空 public boolean isempty() {} // 判断当前顺序表是不是满了 public boolean isFull() {} // 打印顺序表 public void display() {} // 新增元素,默认在数组最后新增 public void add(int data) {} // 新增元素,在数组最前面新增 public void addHead(int data){} // 在 pos 位置新增元素 public void addPos(int pos, int data) {} // 删除表头元素 public void removeHead() {} // 删除表尾元素 public void removeTail() {} // 指定下标元素的删除 public void removePos(int pos) {} //删除第一次出现的关键字key public void remove(int toRemove) {} // 判定是否包含某个元素 public boolean contains(int toFind) { return true; } // 查找某个元素对应的位置 public int indexOf(int toFind) { return -1; } // 获取 pos 位置的元素 public int getPos(int pos) { return -1; } // 给 pos 位置的元素设为 value public void setPos(int pos, int value) {} // 获取顺序表长度 public int size() { return 0; } // 清空顺序表 public void clear() {} } 说明:
private int[] elem;
elem指的是新建立的一个数组;
private int usedSize; // 默认值是0
usedSize指的是数组的有效的长度;(即存储了元素的长度是多少)
private static final int DEFAULT_SIZE = 4; // 定义为常量,更加安全
并且数组的初始化的长度为4;
上述就为顺序表的一些基本实现方法;接下来我们将逐个的讲解这些方法具体是怎么实现的;

三、顺序表基本功能的实现
功能1:
对顺序表进行扩容
// 对顺序表进行扩容 public void expand() { this.elem = Arrays.copyOf(this.elem, this.usedSize * 2); System.out.println("已经成功扩容至原来的两倍"); // 给用户提醒 }解析:
首先我们要知道Arrays中copyOf方法的用法;
Arrays.copyOf方法:
概念:
Arrays.copyOf()的实质其实就是改变数组的长度,实现数组的扩容和缩容。
语法格式:
Arrays.copyOf(original,newLength); original:需要改变的数组名 newLength:数组改变后新的长度代码示例说明:
public static void main(String[] args) { //定义一个初始数组,初始数组的长度为8 int[] a = {1,2,3,4,5,6,7,8}; System.out.println("源数组:"+Arrays.toString(a)); //数组扩容,将数组的长度由8扩展为10 a = Arrays.copyOf(a, 10); System.out.println("缩容后的数组:"+Arrays.toString(a)); }输出结果:
最后我们就通过这个Arrays中copyOf方法完成了扩容的操作;
功能2:
判断顺序表是否为空
/** * 判断当前顺序表是否为空 * @return true->空的,false->还没空 */ public boolean isempty() { if (this.usedSize == 0) { return true; } else return false; }解析:
usedSize表示顺序表的有效长度;所以通过判断usedSize是否为0来实现判断顺序表是否为空的代码实现;
功能3:
判断顺序表是否已满:
/** * 判断当前顺序表是不是满了 * @return true->满了,false->还没满 */ public boolean isFull() { if (this.usedSize == this.elem.length) return true; else return false; }解析:
此处的elem.length表示的是数组的长度;当数组的长度等于顺序表的有效长度时;则说明此顺序表是满的;
功能4:
打印顺序表:
// 打印顺序表 // 打印的第一种方式 public void display() { for (int i = 0; i < this.elem.length; i++) { System.out.print(this.elem[i] + " "); } System.out.println(); } // 打印的第二种方式,用Arrays.toString直接打印 public void display() { System.out.println(Arrays.toString(this.elem)); }解析:
此处通过数组下标的方式来遍历数组;用数组下标与数组的长度对比;
由此来遍历整个顺序表;从而实现打印顺序表;
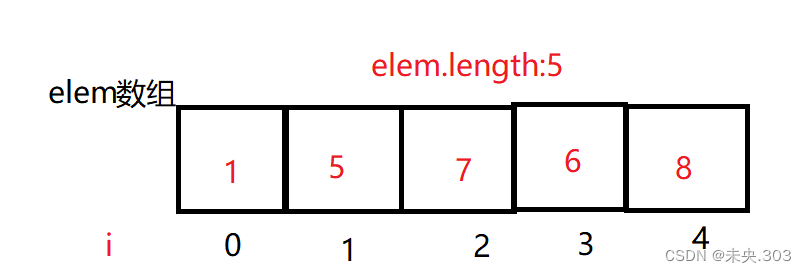
图示解析:
功能5:
获取顺序表的有效长度:
// 获取顺序表的有效长度 public int size() { return this.usedSize; }解析:
直接返回有效长度usedSize即可;
功能6:
清空顺序表
// 清空顺序表 public void clear() { for (int i = 0; i < this.usedSize; i++) { this.elem[i] = 0; } this.usedSize = 0; // 注意有效数组长度也要清零 }解析:
此处的清空顺序表和前面的打印顺序表不一样;
清空顺序表只需要将顺序表里面的有效长度清除即可,不用遍历整个顺序表;
最后注意要将有效数组长度也清零;
图示解析:

四、四大功能
1、增加数据
1.1 头插法:
1 // 新增元素,在数组最前面新增 public void addHead(int data) { if (isFull()) { System.out.println("数组满了,需要扩容"); expand(); } else { // 从usedSize下标开始,不会数组越界(此时的elem.length > usedSize) for (int i = this.usedSize; i > 0; --i) { this.elem[i] = this.elem[i - 1]; // 从后往前挪动数据,为的是给顺序表的表头腾出来 } this.elem[0] = data; // 在顺序表开头插入 this.usedSize++; // 数组有效长度加一 }解析:
1.
在顺序表中插入元素,首先要先 判断顺序表是否满了;
如果满了,需要扩容;如果没有满,则进行插入操作;
所以此处就需要用到前面介绍过的public boolean isFull函数;
代码示例:
if (isFull()) { System.out.println("数组满了,需要扩容"); expand();2.既然实在开头插入,那我们就应该把顺序表中每一个元素向后移动一位,把第一个位置腾空出来,再将需要的数据插入进去;
移动时肯定是先移动后面的元素,然后依次移动前一个元素;
代码示例:
for (int i = this.usedSize; i > 0; --i) { this.elem[i] = this.elem[i - 1]; // 从后往前挪动数据,为的是给顺序表的表头腾出来 }此代码就是实现顺序表中代码依次往后挪动的操作;
图片示例:
1.2 尾插法
//在数组最后新增 public void addTail(int data) { if (isFull()) { System.out.println("数组满了需要扩容"); expand(); } else this.elem[this.usedSize] = data; this.usedSize++; }解析:
1.
插入操作首先要需要 判断顺序表是否满了;
同上面的头插法;
2.
既然是尾插法,就不需要进行元素的移动,直接在有效数据长度的后面插入数据即可;
最后要注意将有效数据长度增加一位(因为多存储了一个数据)
代码示例:
this.elem[this.usedSize] = data; this.usedSize++;
1.3 指定下标插入
// 在 pos 位置新增元素 public void addPos(int pos, int data) { if (pos < 0 || pos > usedSize) { System.out.println("pos位置不合法"); return; } if (isFull()) { System.out.println("数组满了需要扩容"); expand(); } else { // 如果插入位置在顺序表的中间,要注意挪动元素,从后向前挪动,这样不会造成元素值的覆盖 for (int i = this.usedSize - 1; i >= pos; --i) { this.elem[i + 1] = this.elem[i]; } this.elem[pos] = data; // 挪动完毕,可以赋值插入 this.usedSize++; // 当前元素数加一 } }解题思路:
- 判断pos位置是否合法(在顺序表中,数据是连续的,中间不能有空缺)
- 判断顺序表是否满了,如果满了,需要扩容
- 插入数据(可能需要1.挪动数据2.插入数据)
注意:
解析:
1. 判断pos位置是否合法(在顺序表中,数据是连续的,中间不能有空缺)
代码示例:
if (pos < 0 || pos > usedSize) { System.out.println("pos位置不合法"); return; }在数据结构中,每次储存元素必须有一个前驱信息的结点;所以pos>usedSIze;
2.判断顺序表是否满了,如果满了,需要扩容;
这里和上面头插尾插一样,不过多赘述;
3.插入数据(可能需要1.挪动数据2.插入数据)
代码示例:
// 如果插入位置在顺序表的中间,要注意挪动元素,从后向前挪动,这样不会造成元素值的覆盖 for (int i = this.usedSize - 1; i >= pos; --i) { this.elem[i + 1] = this.elem[i]; } this.elem[pos] = data; // 挪动完毕,可以赋值插入 this.usedSize++; // 当前元素数加一图示说明:
当pos=2时;
2、删除数据
2.1 头删
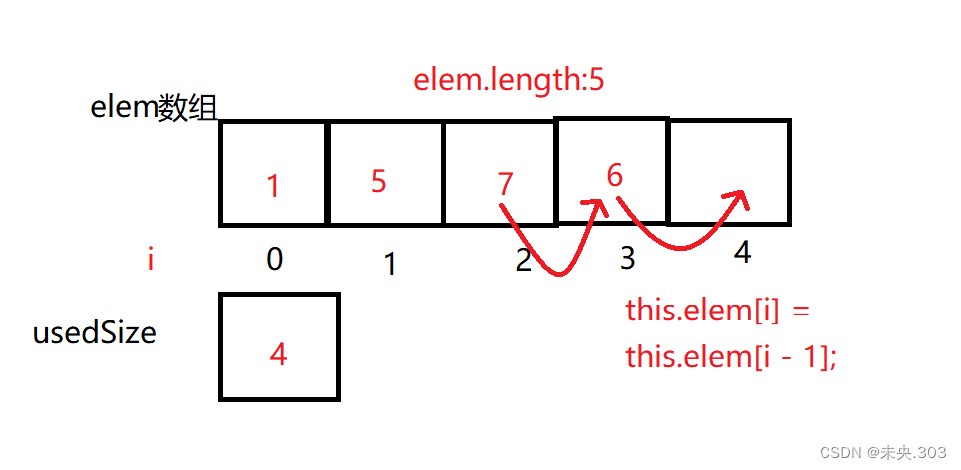
// 删除表头元素 public void removeHead() { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } // 从第一个元素开始,用后面元素的值覆盖掉前面的值,遍历整个数组就相当于把第一个元素用覆盖的方式抹去了 for (int i = 1; i < this.usedSize; i++) { this.elem[i - 1] = this.elem[i]; } this.elem[this.usedSize - 1] = 0; // 现在的最后一个元素是原来的倒数第二个元素, 所以原来的最后一个有效元素要置0 this.usedSize--; // 不要忘记改变有效数组的长度 }解题思路:
首先还是要判断顺序表是否为空的问题;
要想删除第一个元素,我们可以通过从从第一个元素开始,用后面元素的值覆盖掉前面的值,遍历整个数组就相当于把第一个元素用覆盖的方式抹去了;
现在的最后一个元素是原来的倒数第二个元素, 所以原来的最后一个有效元素要置0;
最后不要忘记改变有效数组的长度;
图示说明:
2.2 尾删
// 删除表尾元素 public void removeTail() { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } this.elem[this.usedSize - 1] = 0; // 直接将最后一个元素置0就完成了尾删 this.usedSize--; // 不要忘记改变有效数组的长度 }解析:
首先还是判断顺序表是否为空;
然后既然尾删,那么直接将最后一个有效元素置0即可;elem[this.usedSize - 1] = 0;
最后不要忘记修改有效数组的长度;usedSize--;
2.3 指定下标删除
// 指定下标元素的删除 public void removePos(int pos) { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } if (pos < 0 || pos >= this.usedSize) { System.out.println("pos下标不合法"); } else { for (int i = pos; i < this.usedSize ; i++) { this.elem[i-1] = this.elem[i]; // 从要删除的下标开始,用后边元素的值覆盖掉前面的值,就完成了删除 } this.elem[this.usedSize - 1] = 0; // 要完整的删除,将挪动的最后一个元素的原本位置 置空 this.usedSize--;// 删除后不要忘记更改顺序表的有效长度 } }解题思路:
- 判断pos位置是否合法(在顺序表中,数据是连续的,中间不能有空缺)
- 判断顺序表是否满了,如果满了,需要扩容
- 删除数据(覆盖数据)
解析:
此处和上面指定下标插入一样的讨论情况;
都是先判断合法和是否满了的情况;
最后通过和头删法一样的分析方法,来实现指定下标删除;
2.4 删除首次出现的指定元素
//删除第一次出现的关键字key public void removeKey(int toRemove) { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } for (int i = 0; i < this.usedSize; i++) { if (this.elem[i] == toRemove) { // 注意是this.usedSize - 1,将此时 i 之后的元素统一往前搬移一个位置 for (int j = i; j < this.usedSize - 1; ++j) { this.elem[j] = this.elem[j + 1]; } this.elem[this.usedSize - 1] = 0; // 要完整的删除,将挪动的最后一个元素的原本位置 置空 this.usedSize--; // 删除后不要忘记更改顺序表的有效长度 return; // 只删除第一次出现的 } } }

3、查找数据
3.1 获取指定位置的元素
// 获取 pos 位置的元素 public int getPos(int pos) { if (pos < 0 || pos >= this.usedSize) { // 注意这里当pos==this.usedSize也是不合法的,因为此时的pos下标所要获取的是顺序表中第usedSize+1个元素 System.out.println("pos的位置不合法"); return -1; } else { return this.elem[pos]; } }解题思路:
- 考虑要获取的位置是否合法
- 返回指定位置的元素
解析:
1.要获取这个元素,首先要判断这个元素的位置是否合法;
但此处要注意pos==this.usedSize也是不合法的;因为此时的pos下标所要获取的是顺序表中第usedSize+1个元素;
2.最后直接返回指定位置的元素即可;return this.elem[pos];
3.2 获取指定元素所在的位置
// 查找某个元素所对应顺序表中的位置 public int indexOf(int toFind) { for (int i = 0; i < this.usedSize; i++) { if (this.elem[i] == toFind) { return i; } } System.out.println("在数组中没有找到该元素"); return -1; }解析:
既然要查找一个元素的位置,那么就应该遍历整个顺序表;
代码中的toFind指的是所要查找的元素;
当elem[i] == toFind时候,说明找到了所要查找的元素;否则提示顺序表中找不到所要查找的元素;
3.3 查找表中是否包含某个元素
/** * /判定是否包含某个元素 * @param toFind 要查找的元素 * @return true->包含, false->不包含 */ public boolean contains(int toFind) { for (int i = 0; i < this.usedSize; i++) { if (this.elem[i] == toFind) return true; } return false; }解析:
直接对整个顺序表进行遍历;直到找到所需要找的那个元素为止;this.elem[i] == toFind;
当找到了return ture;否则return fales;

4、修改数据
4.1 修改表中任意位置的元素
// 给 pos 位置的元素设为 value public void setPos(int pos, int value) { if (pos < 0 || pos > this.usedSize) { System.out.println("pos位置不合法"); return; } if (pos == this.usedSize) { // 对这种情况要单独处理,此时相等于增加元素 this.elem[pos] = value; this.usedSize++; } else { this.elem[pos] = value; } }解题思路:
1.首先考虑修改的位置是否合法
2.考虑特殊情况
解析:
value指的是pos位置所放置的元素;
1.首先依旧需要考虑修改位置是否合法;pos < 0 || pos > this.usedSize;
2.然后考虑特殊情况,当pos=this.usedSize时;
此时就相当于新增加了一个元素,类似于前面新增数据的尾插法;

五、代码总结
MyArraysList.java
import java.util.Arrays; public class MyArraysList { private int[] elem; private int usedSize; // 默认值是0 private static final int DEFAULT_SIZE = 4; // 定义为常量,更加安全 // 初始化顺序表 public MyArraysList() { this.elem = new int[4]; } // 对顺序表进行扩容 public void expand() { this.elem = Arrays.copyOf(this.elem, this.usedSize * 2); System.out.println("已经成功扩容至原来的两倍"); // 给用户提醒 } /** * 判断当前顺序表是否为空 * @return true->空的,false->还没空 */ public boolean isempty() { if (this.usedSize == 0) { return true; } else return false; } /** * 判断当前顺序表是不是满了 * @return true->满了,false->还没满 */ public boolean isFull() { if (this.usedSize == this.elem.length) return true; else return false; } // 打印顺序表 public void display() { for (int i = 0; i < this.elem.length; i++) { System.out.print(this.elem[i] + " "); } // System.out.println(Arrays.toString(this.elem));或者用Arrays.toString打印也行 System.out.println(); } // 新增元素,默认在数组最后新增 public void addTail(int data) { if (isFull()) { System.out.println("数组满了需要扩容"); expand(); } else this.elem[this.usedSize++] = data; } // 新增元素,在数组最前面新增 public void addHead(int data) { if (isFull()) { System.out.println("数组满了,需要扩容"); expand(); } else { // 从usedSize下标开始,不会数组越界(此时的elem.length > usedSize) for (int i = this.usedSize; i > 0; --i) { this.elem[i] = this.elem[i - 1]; // 从后往前挪动数据,为的是给顺序表的表头腾出来 } this.elem[0] = data; // 在顺序表开头插入 this.usedSize++; // 数组有效长度加一 } } // 1、判断pos位置是否合法(在顺序表中,数据是连续的,中间不能有空缺) // 2、判断顺序表是否满了,如果满了,需要扩容 // 3、插入数据(可能需要挪作元素) // 在 pos 位置新增元素 public void addPos(int pos, int data) { if (pos < 0 || pos > usedSize) { System.out.println("pos位置不合法"); return; } if (isFull()) { System.out.println("数组满了需要扩容"); expand(); } else { // 如果插入位置在顺序表的中间,要注意挪动元素,从后向前挪动,这样不会造成元素值的覆盖 for (int i = this.usedSize - 1; i >= pos; --i) { this.elem[i + 1] = this.elem[i]; } this.elem[pos] = data; // 挪动完毕,可以赋值插入 this.usedSize++; // 当前元素数加一 } } // 删除表头元素 public void removeHead() { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } // 从第一个元素开始,用后面元素的值覆盖掉前面的值,遍历整个数组就相当于把第一个元素用覆盖的方式抹去了 for (int i = 1; i < this.usedSize; i++) { this.elem[i - 1] = this.elem[i]; } this.elem[this.usedSize - 1] = 0; // 现在的最后一个元素是原来的倒数第二个元素, 所以原来的最后一个有效元素要置0 this.usedSize--; // 不要忘记改变有效数组的长度 } // 删除表尾元素 public void removeTail() { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } this.elem[this.usedSize - 1] = 0; // 直接将最后一个元素置0就完成了尾删 this.usedSize--; // 不要忘记改变有效数组的长度 } // 指定下标元素的删除 public void removePos(int pos) { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } if (pos < 0 || pos >= this.usedSize) { System.out.println("pos下标不合法"); } else { for (int i = pos; i < this.usedSize - 1; ++i) { this.elem[i] = this.elem[i + 1]; // 从要删除的下标开始,用后边元素的值覆盖掉前面的值,就完成了删除 } this.elem[this.usedSize - 1] = 0; // 要完整的删除,将挪动的最后一个元素的原本位置 置空 this.usedSize--;// 删除后不要忘记更改顺序表的有效长度 } } //删除第一次出现的关键字key public void removeKey(int toRemove) { if (isempty()) { System.out.println("顺序表为空,删除不合法"); return; } for (int i = 0; i < this.usedSize; i++) { if (this.elem[i] == toRemove) { // 注意是this.usedSize - 1,将此时 i 之后的元素统一往前搬移一个位置 for (int j = i; j < this.usedSize - 1; ++j) { this.elem[j] = this.elem[j + 1]; } this.elem[this.usedSize - 1] = 0; // 要完整的删除,将挪动的最后一个元素的原本位置 置空 this.usedSize--; // 删除后不要忘记更改顺序表的有效长度 return; // 只删除第一次出现的 } } } /** * /判定是否包含某个元素 * @param toFind 要查找的元素 * @return true->包含, false->不包含 */ public boolean contains(int toFind) { for (int i = 0; i < this.usedSize; i++) { if (this.elem[i] == toFind) return true; } return false; } // 查找某个元素对应的位置 public int indexOf(int toFind) { for (int i = 0; i < this.usedSize; i++) { if (this.elem[i] == toFind) { return i; } } System.out.println("在数组中没有找到该元素"); return -1; } // 获取 pos 位置的元素 public int getPos(int pos) { if (pos < 0 || pos >= this.usedSize) { System.out.println("pos的位置不合法"); return -1; } else { return this.elem[pos]; } } // 给 pos 位置的元素设为 value public void setPos(int pos, int value) { if (pos < 0 || pos > this.usedSize) { System.out.println("pos位置不合法"); return; } if (pos == this.usedSize) { // 对这种情况要单独处理,此时相等于增加元素 this.elem[pos] = value; this.usedSize++; } else { this.elem[pos] = value; } } // 获取顺序表长度 public int size() { return this.usedSize; } // 清空顺序表 public void clear() { for (int i = 0; i < this.usedSize; i++) { this.elem[i] = 0; } this.usedSize = 0; // 注意有效数组长度也要清零 } }
Test.java
/** * 对顺序表进行测试的代码 */ public class Test { public static void main(String[] args) { MyArraysList myArraysList = new MyArraysList(); // 尾插四个数字 myArraysList.addTail(12); myArraysList.addTail(32); myArraysList.addTail(17); myArraysList.addTail(32); // 进行扩容 myArraysList.expand(); // 指定在pos位置新增元素 myArraysList.addPos(1, 777); // 打印当前的顺序表 System.out.print("第一次测试的顺序表为:"); myArraysList.display(); // 删除顺序表中首次出现的元素32 myArraysList.removeKey(32); // 获取顺序表中 1下标的元素值 int tmp = myArraysList.getPos(1); System.out.println("顺序表中下标为1的元素的值为:" + tmp); // 给顺序表中1下标的元素设为value myArraysList.setPos(1, 100); // 打印此时的顺序表 System.out.print("修改后第二次测试的顺序表为:"); // 此时1下标的值为100 myArraysList.display(); // 顺序表此时的有效长度 System.out.println("顺序表的有效长度为:" + myArraysList.size()); // 清空顺序表 myArraysList.clear(); System.out.print("第三次测试的顺序表为:"); myArraysList.display(); System.out.println("清空顺序表后,顺序表的有效长度为:" + myArraysList.size()); } }
测试结果:
总结
今天我们学习了数据结构的第一种顺序表的学习,下一节内容我们将进入到链表的学习,本节学习会让我们为后面的学习打下好的基础,所以说必须要能够熟练的掌握!!!!!!!!!!