目录
前言:
什么是集合
集合的三大特性
1.集合的创建
(1)直接创建
(2)强制转换
2.集合的添加
(1)add()函数
(2)update() 函数
3.集合元素的删除
(1)remove() 函数
(2)discard() 函数
4.集合的运算
5.集合的应用----对列表去重
前言:
上一期讲了无序序列中的字典相关操作Python学习-----无序序列1.0(字典的创建、查看、添加、修改、删除/替换)_守约斯维奇的博客-CSDN博客 这一期来讲讲无序序列中的集合(set)的操作,包括创建、添加、删除已经集合之间的运算。
什么是集合
和数学中的集合概念一样,用来保存不重复的元素,即集合中的元素都是唯一的,互不相(高中都学过集合了,懂的都懂)
集合的三大特性
无序性
唯一性
互异性
1.集合的创建
(1)直接创建
格式:
集合名 = {元素,元素,元素……}
注意事项:集合是可变的(可以修改、添加、删除等等),但是里面的元素性质是不可变的,所以集合里面的元素不可以是列表类型、字典类型或者集合类型
示例1:(集合的无序性)
s={1,'qq',1.9,False}
print(s)
#输出结果:{'qq', 1, 1.9, False}集合本身是无序性的,所以输出结果也是没有按照顺序的,是随机顺序
示例2:(集合的互异性和唯一性)
s={1,1,2,2,2,1.6,False}
print(s)
#输出结果:{False, 1, 2, 1.6}这里面的1和2栋出现了重复,但是输出结果都是只保留了一个,这也是集合的互异性和唯一性
(2)强制转换
这里有一个问题,如果我想创建一个空集合怎么办,前面说了创建空字典直接 d = {},就行了,但是集合可不能用花括号,所以这里必须用强制转换set() 函数来实现
示例1:
#创建空字典 d={}
#创建空集合
s = set()
print(s,type(s))
#输出结果:set() <class 'set'>示例2:
#强制转换把其他类型转换为集合
li=[1,2,5,3.5,False,(1,9.6)]
print(li,type(li))
#输出结果:[1, 2, 5, 3.5, False, (1, 9.6)] <class 'list'>
s=set(li)
print(s,type(s))
#输出结果:{False, 1, 2, 3.5, 5, (1, 9.6)} <class 'set'>2.集合的添加
(1)add()函数
格式:
集合名.add(元素)
添加方式:一次只能添加一个元素
集合本身是无序序列的,所以添加的元素的位置也是随机的放入一般都是用add() 函数去添加
示例1:
s = {1,2,3,3.14}
print(s)
s.add(False)
s.add('集合')
print(s)
示例2:
#通过循环来实现添加多个元素
s = {1,2,3,3.14}
q = {'瓦达西瓦','欧尼酱','空你几哇'}
for i in q:
s.add(i)
print(s)
#输出结果:{1, 2, 3.14, 3, '空你几哇', '欧尼酱', '瓦达西瓦'}(2)update() 函数
格式:
集合.update([元素])
添加方式:这个函数可以添加单个元素,也可以一次性添加多个元素(添加多个元素比add() 函数简单,不需要用到循环)
注意事项:之前在字典的添加也用到了这个函数,但是添加字典是用花括号{}的,而添加集合里面是用中括号[ ] 的
s = {'李信','李华','李白'}
s.update(['瑶','澜'])
print(s)
#输出结果:{'瑶', '李白', '澜', '李信', '李华'}
3.集合元素的删除
(1)remove() 函数
格式:
集合名.remove(元素)
注意:一次性只可以移除一个元素,当元素不存在的时候将会报错
s = {'李信','李华','李白','瑶'}
s.remove('李华')
print(s)
#输出结果:{'瑶', '李信', '李白'}(2)discard() 函数
格式:
集合名.discard(元素)
注意: 当元素不存在的时候 不会报错(这也是与remove函数的区别)
s = {'李信','李华','李白','瑶'}
s.discard('瑶')
print(s)
#输出结果:{'李华', '李白', '李信'}4.集合的运算
| 符号 | 含义 |
|---|---|
| & | 交集,获得两个集合的公共元素 |
| | | 并集,获得两个集合的全部元素 |
| - | 差集,获得前面集合独有的元素 |
| ^ | 对称差集,获得两个几个除公共元素外的多有元素(并集-交集) |
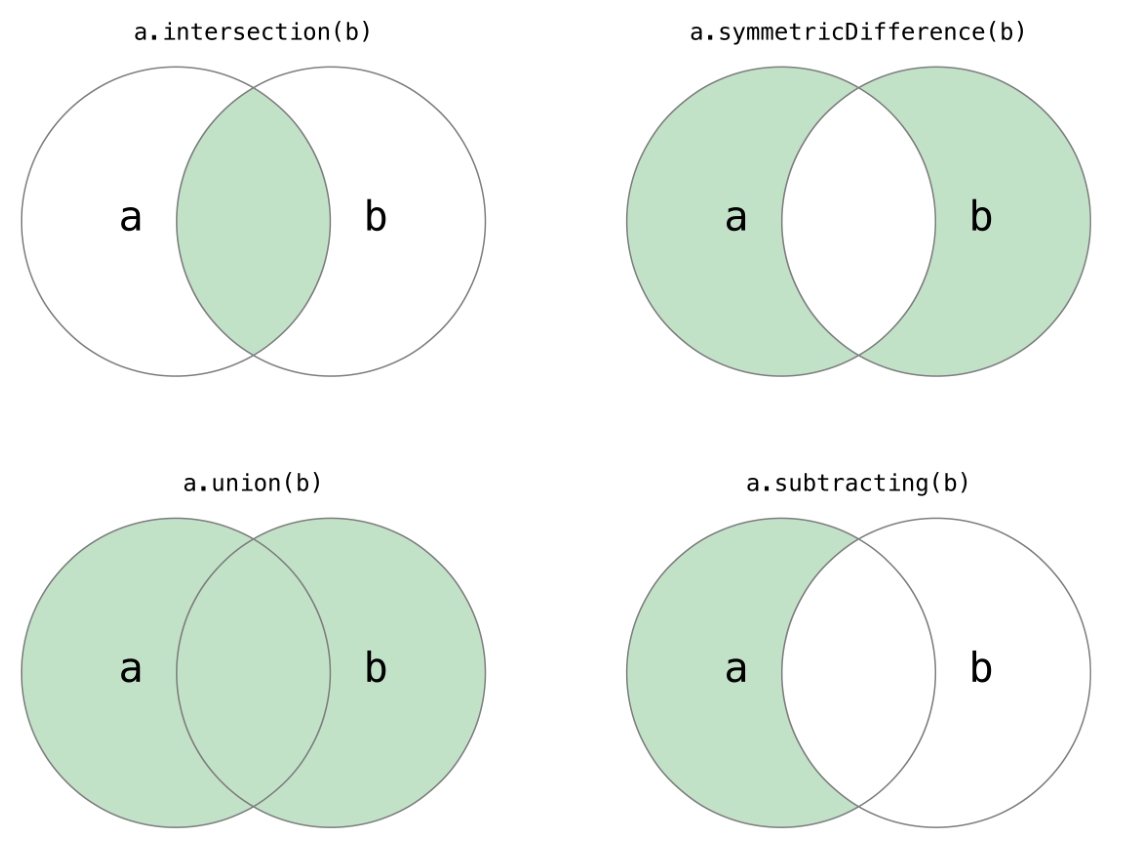
集合的运算跟高中我们学的基本上是一模一样的,交集、并集、补集。我不多解释了,看例题吧。
a = {1, 2, 4, 5, 6}
b = {1, 3, 5, 7}
print(a-b) #a对b的差集 a除去a与b重复的部分
print(b-a) #b对a的差集 b除去a与b重复的部分
print(b&a) #交集--a与b重复的部分
print(b|a) #并集--a与b的全部
print(a^b) # 等效于(a-b)|(b-a)
print((a-b)|(b-a)) 
集合运算很简单了,就不多讲了,多试试几个就行了
5.集合的应用----对列表去重
集合是有互异性的,唯一性的,如果出现重复的话,那么集合会舍弃重复的部分,只保留一个,所以我们可以通过集合的性质来实现去重,就以列表为例:
li=[1,1,5,5,'蔡徐坤',False]
print(li)
li=set(li)#转换为集合
print(li)
li=list(li)#转换回列表类型
print(li)
OK,这一期就到这里了,下课!!!