【GPLT 二阶题目集】L2-044 大众情人

news2025/1/18 2:11:42

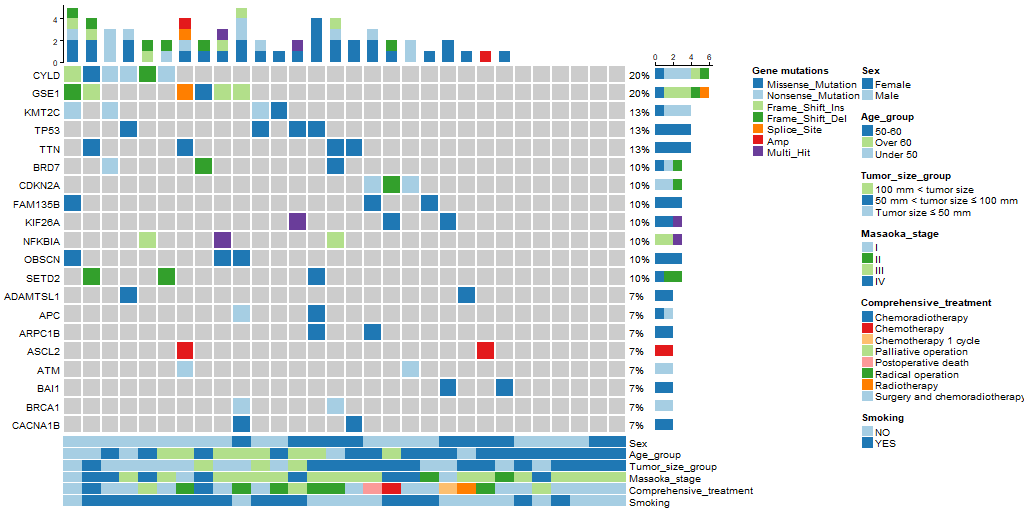
人与人之间总有一点距离感。我们假定两个人之间的亲密程度跟他们之间的距离感成反比，并且距离感是单向的。例如小蓝对小红患了单相思，从小蓝的眼中看去，他和小红之间的距离为 1，只差一层窗户纸；但在小红的眼里，她和小蓝之间的距离为 108000，差了十万八千里…… 另外，我们进一步假定，距离感在认识的人之间是可传递的。例如小绿觉得自己跟小蓝之间的距离为 2，则即使小绿并不直接认识小红，我们也默认小绿早晚会认识小红，并且因为跟小蓝很亲近的关系，小绿会觉得自己跟小红之间的距离为 1+2=3。当然这带来一个问题，如果小绿本来也认识小红，或者他通过其他人也能认识小红，但通过不同渠道推导出来的距离感不一样，该怎么算呢？我们在这里做个简单定义，就将小绿对小红的距离感定义为所有推导出来的距离感的最小值。

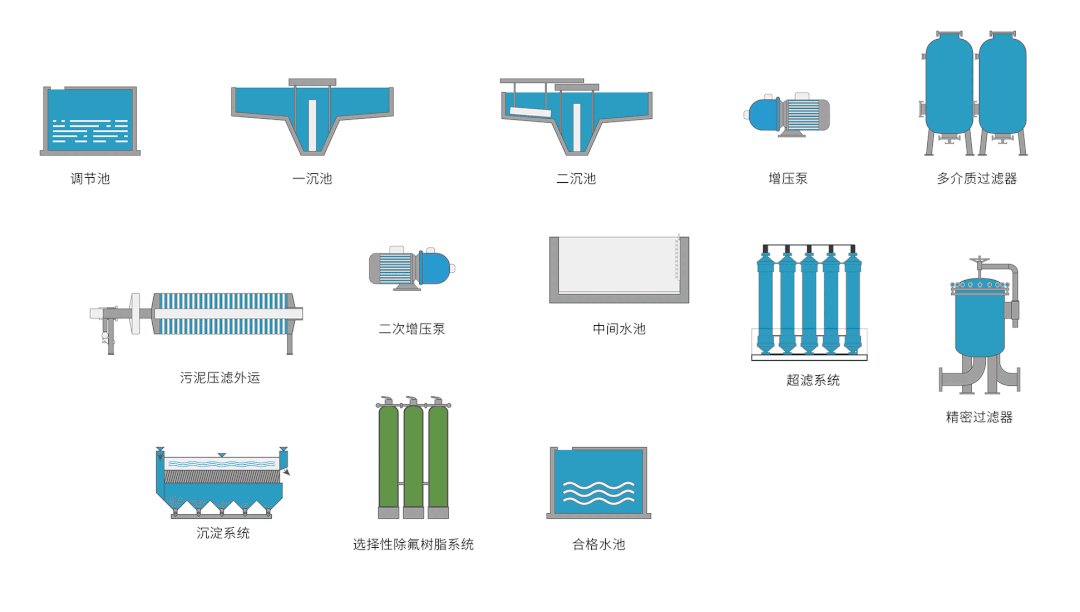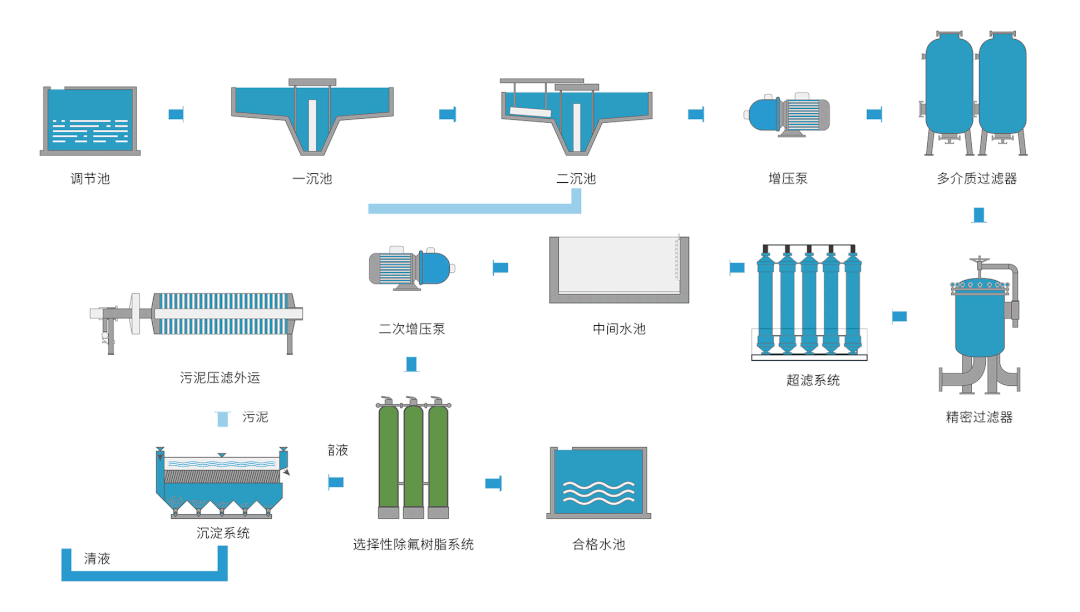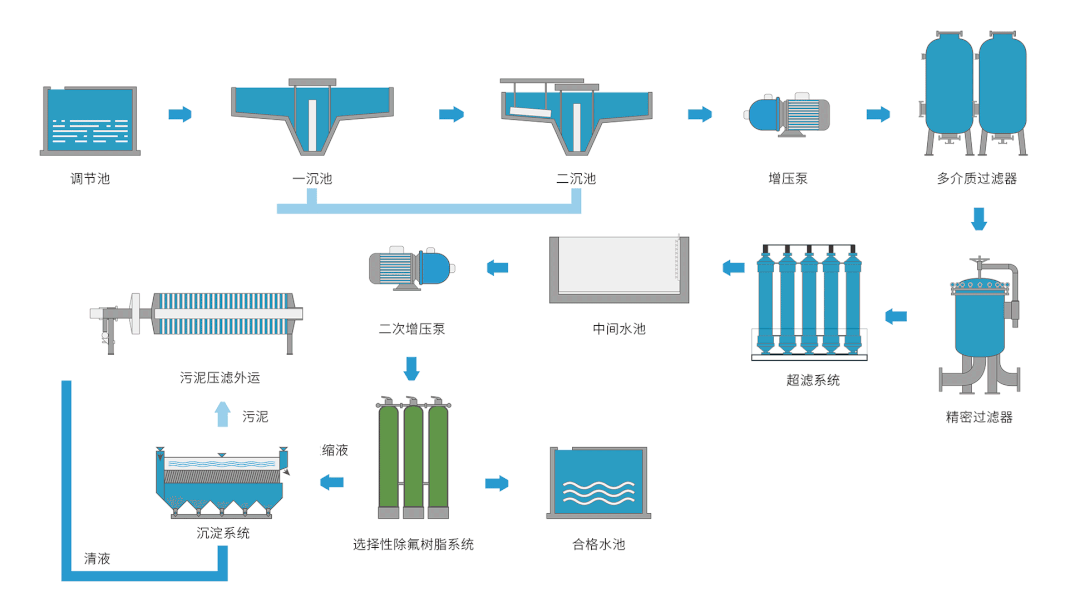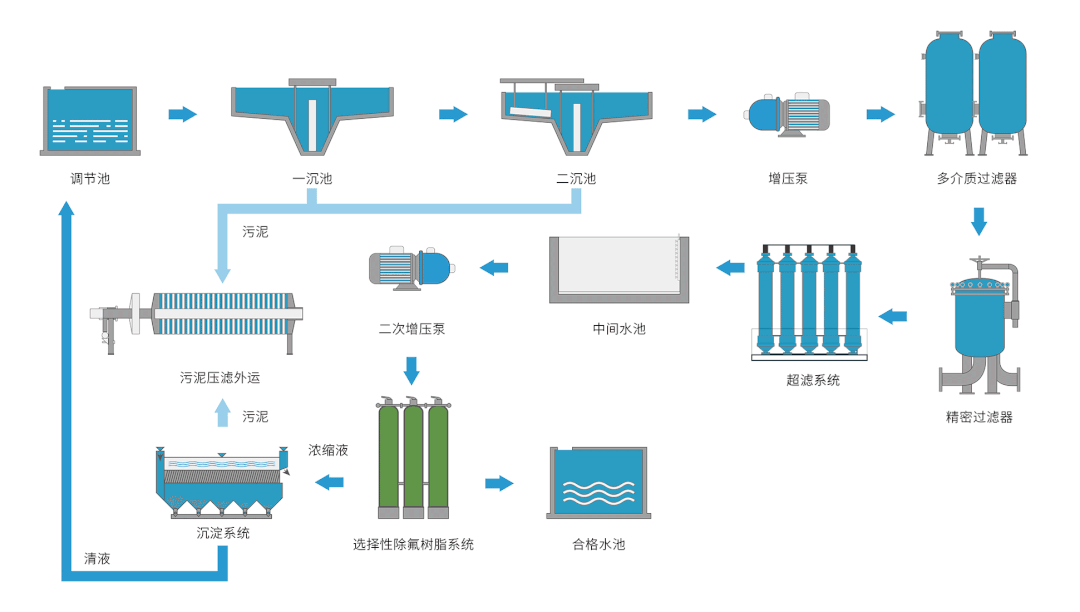
输入格式：

输入在第一行中给出一个正整数 N（≤500），为总人数。于是我们默认所有人从 1 到 N 编号。

随后 N 行，第 i 行描述了编号为 i 的人与其他人的关系，格式为：
性别 K 朋友1:距离1 朋友2:距离2 …… 朋友K:距离K
其中性别是这个人的性别，F 表示女性，M 表示男性；K（<N 的非负整数）为这个人直接认识的朋友数；随后给出的是这 K 个朋友的编号、以及这个人对该朋友的距离感。距离感是不超过 10^6 的正整数。

题目保证给出的关系中一定两种性别的人都有，不会出现重复给出的关系，并且每个人的朋友中都不包含自己。

输出格式：

第一行给出自身为女性的“大众情人”的编号，第二行给出自身为男性的“大众情人”的编号。如果存在并列，则按编号递增的顺序输出所有。数字间以一个空格分隔，行首尾不得有多余空格。

输入样例：

6
F 1 4:1
F 2 1:3 4:10
F 2 4:2 2:2
M 2 5:1 3:2
M 2 2:2 6:2
M 2 3:1 2:5

输出样例：

2 3
4

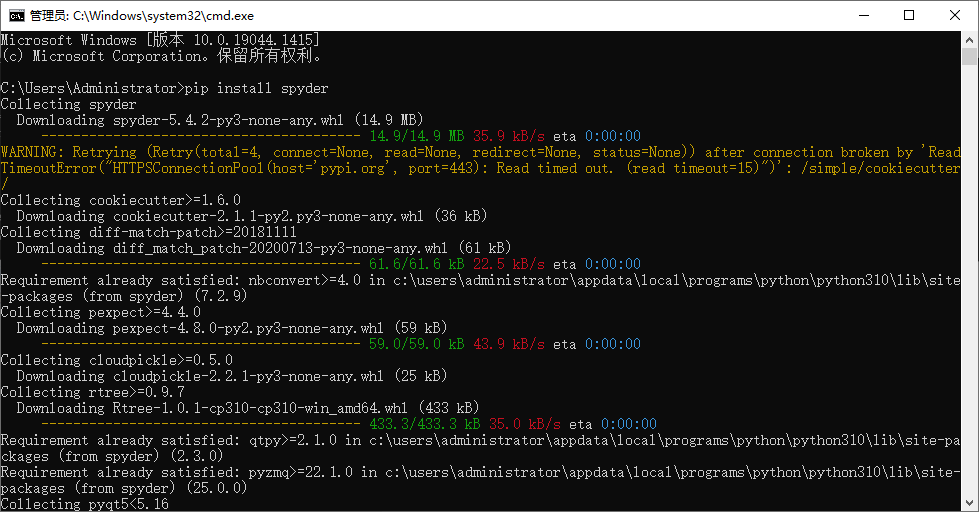
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

const int N = 510;
//MAX表示无限大，其值不能太大也不能太小
//太小影响距离计算，太大可能导致距离数值越界变负数
const int MAX = 0x3f3f3f3f;
//const int MAX = 1e6 + 10; //测试点3运行错误（万恶的21分！！！）
char sex[N]; //性别
int dp[N][N]; //dp[i][j]指i在j眼中的距离感（要求最小）

class node
{
public:
    int num;
    int dist;
};
vector<node> m, f; //男性，女性异性缘的倒数

bool cmp(node a, node b)
{
    if (a.dist != b.dist)
        return a.dist < b.dist;
    return a.num < b.num;
}

int main()
{
    int n, k, a, b; cin >> n;
    for (int i = 1; i <= n; i++) //距离感初始化
        for (int j = 1; j <= n; j++)
            if (i == j)
                dp[i][j] = 0;
            else
                dp[i][j] = MAX;
    for (int i = 1; i <= n; i++) //获取性别和距离感
    {
        cin >> sex[i] >> k;
        while (k--)
        {
            scanf("%d:%d", &a, &b);
            dp[a][i] = b;
        }
    }
    for (int x = 1; x <= n; x++) //Floyd算法
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                dp[i][j] = min(dp[i][j], dp[i][x] + dp[x][j]);
    for (int i = 1; i <= n; i++) //获取异性中的最大距离感
    {
        node temp = { i,0 };
        for (int j = 1; j <= n; j++)
        {
            if (sex[i] != sex[j] && dp[i][j] > temp.dist)
                temp.dist = dp[i][j];
        }
        if (sex[i] == 'M')
            m.push_back(temp);
        else
            f.push_back(temp);
    }
    sort(m.begin(), m.end(), cmp);
    sort(f.begin(), f.end(), cmp);
    cout << f[0].num;
    for (int i = 1; i < f.size(); i++)
    {
        if (f[i].dist == f[0].dist)
            cout << " " << f[i].num;
        else
            break;
    }
    cout << endl << m[0].num;
    for (int i = 1; i < m.size(); i++)
    {
        if (m[i].dist == m[0].dist)
            cout << " " << m[i].num;
        else
            break;
    }
    return 0;
}