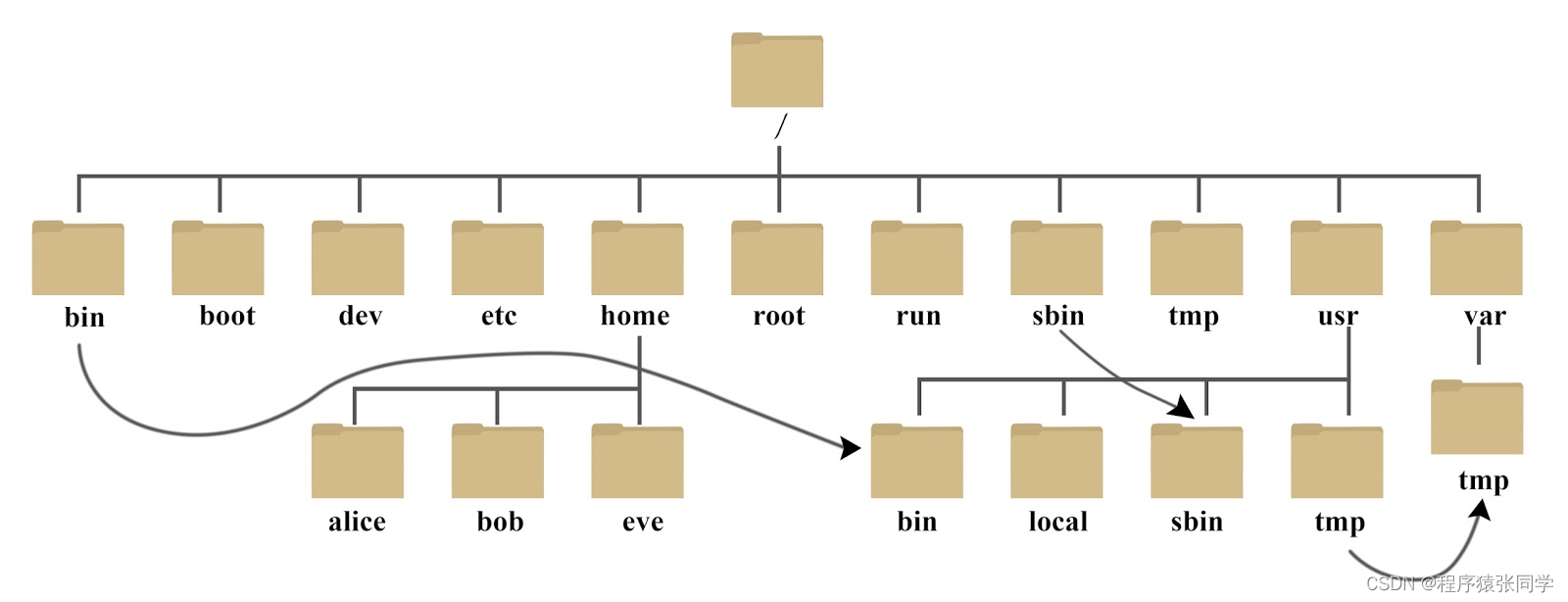
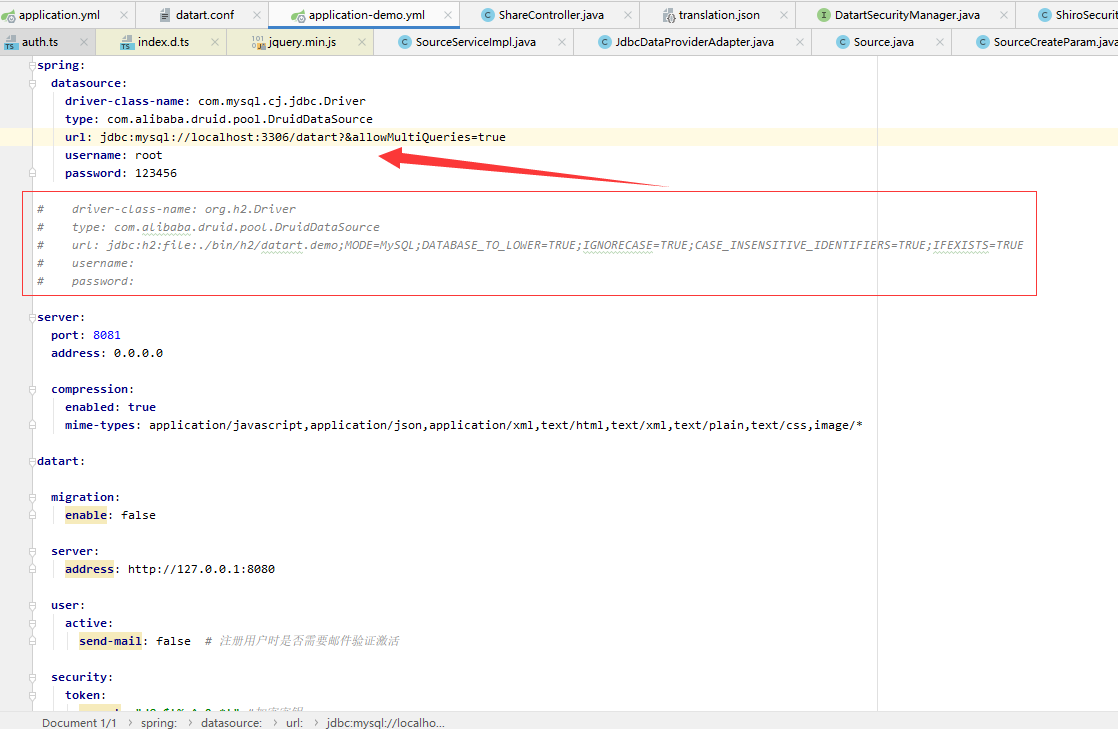
0. 简介
对于激光SLAM来说,现在越来越多的算法不仅仅局限于点线等简答特征的场景了,文章《PLC-LiSLAM: LiDAR SLAM With Planes, Lines,and Cylinders》说到,平面、线段与圆柱体广泛存在于人造环境中。为此作者提出了一个使用这些landmark的激光雷达SLAM系统。目前已有工作做了类似于BA的平面adjustment(即.PA),但是这类工作在缺少平面的场景效果很差,为了增强系统的鲁棒性,引入更多的特征是有必要的,因此作者在本文中引入了额外的线和圆柱体特征,并且实现了平面-线-圆柱体的adjustment即(PLCA),PLCA不依赖于从三维特征点捕获的点数,这使得高效求解大规模PLCA问题成为可能。定位部分通过将局部平面、直线和柱面与全局平面、直线和柱面来进行配准,从而进行实时姿态估计,这种被称为平面-直线-柱面配准(PLCR, plane-line-cylinder registration)。在检测landmark并完成数据关联的过程中很可能会引入误检。本文通过检查后端的成本(cost)函数来纠正这些错误,这个错误纠正机制是那些基于配准的方法。例如LOAM和ICP,由于它们并不维护数据间的关联关系,所以很难纠正这些错误。这里由于该论文没有预印本,所以作者以附录的形式展示了本文的内容。由于本文的内容较多,所以作者主要来讲解特征提取这块的内容。其余的用泡泡机器人的内容作为补充。
1. 文章贡献
在之前的工作[1],[2]中,我们探索了激光雷达SLAM的平面,并引入平面调整(PA,plane adjustment)来纠正漂移,这是视觉SLAM中的bundle adjustment(BA)的对应。由于只考虑平面,如果没有足够的平面进行姿态估计,这些方法将失败。本文扩展了我们[2]工作的内容,并加入了线条和圆柱体。具体来说,该算法包括局部映射、全局映射和定位三个部分。在局部和全局映射中,通过位姿联合优化平面、直线和圆柱体。我们将由此产生的最小二乘问题分别称为局部和全局平面-柱面调整(PLCA)。在定位中,通过使用平面、直线和柱面进行扫描到模型的连续时间配准来估计新的激光雷达扫描的姿态,称为连续时间平面-直线-柱面配准(PLCR)。本文的贡献如下:
-
本文证明,通过一些预处理,PLCA问题的求解与面、线以及圆柱体里的三维点的数量无关。因为这些landmark的表示是无边界的,许多三维点都会被包含在这些landmark里面。对于求解大尺度的PLCA问题,我们的方法行而有效。
-
本文提供了一个高效的PLCR问题求解方法。我们使用一阶泰勒展开来近似旋转,考虑到两帧之间的旋转一般是足够小的。如果比较大的旋转发生在两帧之间,我们进行迭代近似。
-
本文的算法能够容忍足够的检测误检测。因为遮挡以及激光雷达点云的稀疏性,检测这些landmark的过程容易引入误检测。这个错误纠正机制是那些基于配准的方法,例如LOAM以及ICP很难做到的,因为他们并不维护数据关联。我们的算法通过检验后端的cost来纠正这些误检测。
2. 详细内容
2.1 前后端概念
-
位姿:这个公式表示通过转换矩阵 X = [ R t 0 1 ] ∈ S E ( 3 ) X = \left[ \begin{matrix} R&t\\0&1\end{matrix}\right]∈SE(3) X=[R0t1]∈SE(3)将局部LiDAR坐标系中的点坐标转换到全局坐标系中的一个姿态。其中 ∈ S O ( 3 ) ∈SO(3) ∈SO(3)为旋转矩阵, t ∈ R 3 t∈\mathbb{R}^3 t∈R3为平移向量。在PLCR和PLCA中, x x x参数为 x = [ ω ; t ] x = [ω;t] x=[ω;t],其中 ω ω ω代表了 R R R的角轴(angle-axis)表示形式:
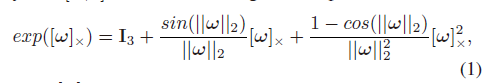
其中 [ ω ] × [ω]_× [ω]×表示 ω ω ω的斜对称矩阵, ∣ ∣ ω ∣ ∣ 2 ||ω||_2 ∣∣ω∣∣2表示 ω ω ω的 L 2 L^2 L2范数。 -
平面:本文中的平面通过一个四维向量表示。前三维表示该平面的法向量,模长为1,最后一维为坐标系原点到该平面的距离。我们将平面表示为 π = [ n ; d ] π = [\mathbf{n};d] π=[n;d],其中 n \mathbf{n} n为 ∣ ∣ n ∣ ∣ 2 = 1 ||\mathbf{n}||_2 = 1 ∣∣n∣∣2=1的平面法线, ∣ d ∣ |d| ∣d∣为原点到该平面的距离。在PLCA中, π π π用最近点参数化 η = d n η = d\mathbf{n} η=dn表示[27]。
-
线:本文中的直线通过一个六维向量表示。前三维表示该直线的方向,后三维表示从原点出发的,垂直于该直线的向量,并且其模长为原点到直线的距离。文中用普吕克坐标(Plücker坐标)[28]表示一条三维空间中的直线,它是一个六维向量 l = [ d ; m ] l = [d;m] l=[d;m],其中 d d d是 l l l的方向, ∣ ∣ d ∣ ∣ 2 = 1 ||d||_2 = 1 ∣∣d∣∣2=1, m m m垂直于由原点和 l l l确定的平面, ∣ ∣ m ∣ ∣ 2 ||m||_2 ∣∣m∣∣2等于从原点到 l l l的距离, l l l有四个自由度。在PLCA中,我们采用[29]中引入的方法对 l l l进行参数化。具体来说,给定 l l l,我们首先构造一个旋转矩阵 R l = [ d , m ∣ ∣ m ∣ ∣ 2 , d × m ∣ ∣ m ∣ ∣ 2 ] R^l = [d, \frac{m}{||m||_2}, d × \frac{m}{||m||_2}] Rl=[d,∣∣m∣∣2m,d×∣∣m∣∣2m],其中 × × ×为叉积。假设 ω l ω^l ωl是(1)中 R l R^l Rl的角轴表示,我们可以用一个四维向量将 l l l参数化 ζ = [ ω l ; ∣ ∣ m ∣ ∣ 2 ] ζ = \left[ω^l; | |m| |_ 2 \right] ζ=[ωl;∣∣m∣∣2]。
-
圆柱体:本文中的圆柱体通过一个七维向量表示,前六维为该圆柱体所在的直线表示(同上),最后一维为该圆柱体的半径。文中将圆柱体表示为 c = [ l c ; r ] c = [l^c;r] c=[lc;r],其中 l c l^c lc为 c c c中线的Plücker坐标, r r r为其半径。在PLCA中,我们通过一个五维向量 ν = [ ζ c ; r ] ν = \left[ζ^c;r\right] ν=[ζc;r]来完成参数化;其中 ζ ζ ζ是上面定义的 l c l^c lc的参数化。
-
观察:用 m m m表示平面、直线或圆柱体,即 m ∈ { π , l , c } m∈\{π, l, c\} m∈{π,l,c}。其中 m j m_j mj表示为第 j j j个landmark特征点信息。并且认为 m j m_j mj在 X i X_i Xi处是可观测的, m j m_j mj在 X i X_i Xi处的观测值形成一组 N i j m N^m_{ij} Nijm点,表示为 P i j m = { p i j k m } k = 1 N i j m \mathbb{P}^m_{ij} = \{p^m_{ijk}\}^{N^m_{ij}} _{k=1} Pijm={pijkm}k=1Nijm。我们将 p i j k m p^m_{ijk} pijkm的齐次坐标表示为 p ~ i j k m = [ p i j k m ; 1 ] \tilde{p}^m_{ijk} = [p^m_{ijk}; 1] p~ijkm=[pijkm;1]。将 P i j m \mathbb{P}^m_{ij} Pijm中各点的同质坐标堆叠起来,我们就会得到一个 P i j m × 4 \mathbb{P}^m_{ij}× 4 Pijm×4的矩阵
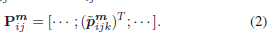
由于平面、直线和圆柱体是无界物体, N i j m N^m_{ij} Nijm可能非常大,这导致了大规模的最小二乘问题。 -
优化:Levenberg-Marquardt(LM)[30]算法通常用于解决最小二乘问题。给定一个最小二乘问题 χ ^ = arg min ∣ ∣ ( χ ) ∣ ∣ 2 2 \hat{χ} = \arg\min||(χ)||^2_2 χ^=argmin∣∣(χ)∣∣22,LM算法在第 k k k次迭代时通过 χ k + 1 = χ k + Δ χ_{k+1} = χ_{k} + Δ χk+1=χk+Δ更新解决方案。这里的 Δ Δ Δ是以下线性方程组的解
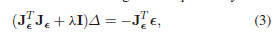
其中 J ε J_\varepsilon Jε是在 χ k χ_k χk处的雅各布矩阵, λ λ λ是LMalgorithm的参数,在每次迭代时都要调整,以确保 ∣ ∣ ( χ ) ∣ ∣ 2 2 ||(χ)||^2_2 ∣∣(χ)∣∣22的值减少。为了应用LM算法,我们通常先计算 J ε J_\varepsilon Jε和 ε \varepsilon ε,然后将其代入(3)来计算 Δ Δ Δ。 因为 N^m_{ij}可能非常大,这种直接的方法可能是计算上的要求。另一方面,显而易见的是 只需要 J ε T J ε J_\varepsilon^TJ_\varepsilon JεTJε和 J ε T ε J_\varepsilon^T \varepsilon JεTε就可以得到 v a r D e l t a varDelta varDelta。我们表明 PLCA的 J ε T J ε J_\varepsilon^TJ_\varepsilon JεTJε和 J ε T ε J_\varepsilon^T \varepsilon JεTε有特殊的结构,可以用来加速计算。用来加速计算。
-
二次方形式:一个对称矩阵 A = [ a i j ] ∈ R n × n A=[a_{ij}]∈\mathbb{R}^{n×n} A=[aij]∈Rn×n决定了一个二次形式 q A = y T A y q_A=y^TAy qA=yTAy,其中 y = [ y 1 ; . . . ; y n ] y=[y1; ...; yn] y=[y1;...;yn]。我们可以把 q A q_A qA写成
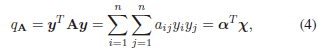
其中 χ = [ − − − ; y i y j ; − − ] ( i ≤ j ) , α = [ − − − ; c i j a i j ; − − ] χ = [ - - - ; y_iy_j ; - - ] (i ≤ j),α = [ - - - ; c_{ij}a_{ij} ; - - ] χ=[−−−;yiyj;−−](i≤j),α=[−−−;cijaij;−−] (如果 i = j i = j i=j, c i j = 1 c_{ij} = 1 cij=1,并且 ( i < j ) , c i j = 2 (i < j),cij = 2 (i<j),cij=2)。 -
矩阵计算:假设 z = [ z 1 ; . . . ; z m ] z = [z1; ...; zm] z=[z1;...;zm], z z z是上面定义的 y y y的向量函数。假设 P ∈ R k × m P∈\mathbb{R}^{k×m} P∈Rk×m是一个恒定的 k × m k×m k×m矩阵。让我们定义 f = P z f = P_z f=Pz,并将 f f f的雅各布矩阵表示为 J f J_f Jf。根据矩阵计算规则, J f J_f Jf的形式为
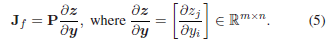
这里 ∂ z ∂ y \frac{∂_z}{∂_y} ∂y∂z是一个 m × n m×n m×n的矩阵, ∂ z j ∂ y i \frac{∂_{z_j}}{∂_{y_i}} ∂yi∂zj是 ∂ z ∂ y \frac{∂_z}{∂_y} ∂y∂z的第 i i i行和第 j j j列的条目。
2.2 系统总览
本文提出的系统由前端与后端组成,前端检测面、线与圆柱体,并建立局部到全局的数据关联,从而进行后续的位姿估计。前端也决定了什么时候一个新的关键帧应当被创建。后端包括局部与全局的PLCA。局部的PLCA通过滑窗优化位姿与landmark。全局的PLCA优化所有的PLCA以及除了第一帧外的所有位姿。当有Landmark被再次观测到时,全局的PLCA便会被触发。

2.3 前端
-
Landmark检测:对激光雷达每一条线的数据进行切分:类似于LOAM,计算每个三维点的曲率,并将属于edge点的部分提取出来,组成集合 E \mathbb{E} E。以每条线上每两个edge点作为两端,可以把这条线分为许多段,这些段里的点为平坦点,组成集合 F \mathbb{F} F。
平面与圆柱体检测:对于每个线上的每段平坦点,寻找与其相近的,但不属于同一条线上的平坦点,如果用RANSAC法拟合平面的平均误差比较小,则利用平面模型来拟合,否则用圆柱体来拟合这些点。
直线检测:对每个段里的edge点,找到所有与其相近的,但属于另一条线的edge点 p p p。利用这两个点可以求得直线方程。对 p p p点再寻找一个在其他线的最近点 p 2 p_2 p2。如果 p 2 p_2 p2到该直线的距离足够小,则利用这三个点来拟合一条直线。重复这个过程直到没有点能够被加入到直线中。
-
Landmark关联
当新一帧点云获得后,首先计算属于该帧的集合 E \mathbb{E} E与集合 F \mathbb{F} F。并对这两个集合分别构建KD-tree。对上一帧里的每个点 p p p,寻找其在当前帧的 n n n个最近点。如果 p p p属于面或者圆柱体,则这 n n n个最近点都被保留,如果 p p p属于直线,则保留这n个点的曲率最大的一个点。随后,利用RANSAC算法找到符合模型的内殿。通过这些内点,我们之后会使用PLCR方法来进行位姿估计。 -
关键帧创建
受到ORB-SLAM的启发,当以下情况发生时,新的关键帧会被创建:- 当前帧20%以上的点不能被追踪与关联。
- 当前帧与上一个关键帧的旋转角度大于5°。
- 当前帧与上一帧的距离大于设定的阈值。
对于新的关键帧,我们在没被关联到的三维点上检测面、线与圆柱体。对于新检测出来的landmark,首先会寻找与已有的landmark的均方根之差,如果大于设定的阈值,则新增一个landmark。
2.4 面-线-圆柱体 联合优化 (PLCA)
-
全局PLCA
在全局的PLCA中,对所有点计算点到模型的损失,从而构建优化问题来同时优化位姿与landmark的参数。作者详细给出了各个模型的LM优化时的参数的形式,有兴趣的同学可以阅读原文,这里不再赘述。
作者证明,构建优化问题Ax=b时,A的规模仅与Landmark的数量有关,而与landmark里的点的数量无关。