涉及知识点

• 三重积分
• 球面坐标系
• 点火公式
• 一些常见积分处理手法

球面坐标系定义

球面坐标系由方位角$\phi$、仰角$\theta$和距离$r$构成

直角坐标系$(x,y,z)$到球面坐标系的$(r,\phi ,\theta )$的转化规则如下：

$$\{\begin{array}{rlr}x& =& r\sin \phi \cos \theta \\ y& =& r\sin \theta \sin \phi \\ z& =& r\cos \phi \end{array}$$

适用

适用于积分区域为球或球的部分、锥或锥的部分。

处理方法

按规则直角坐标系的积分式转换成球面坐标系就行

$$\underset{\Omega }{\iiint }f(x,y,z)dxdydz=\underset{\Omega }{\iiint }f(r\sin \phi \cos \theta ,r\sin \theta \sin \phi ,r\cos \phi )r^2\sin \phi d\theta d\phi dr$$

然后一般按如下顺序写出积分式：

$$\int d\theta \int d\phi \int f(r,\theta ,\phi )dr$$

由于“后积先定限”，所以先处理方位角，即下图中1的轨迹，随后处理仰角，即下图中2的轨迹，两个角取值范围都是$[0,2\pi ]$

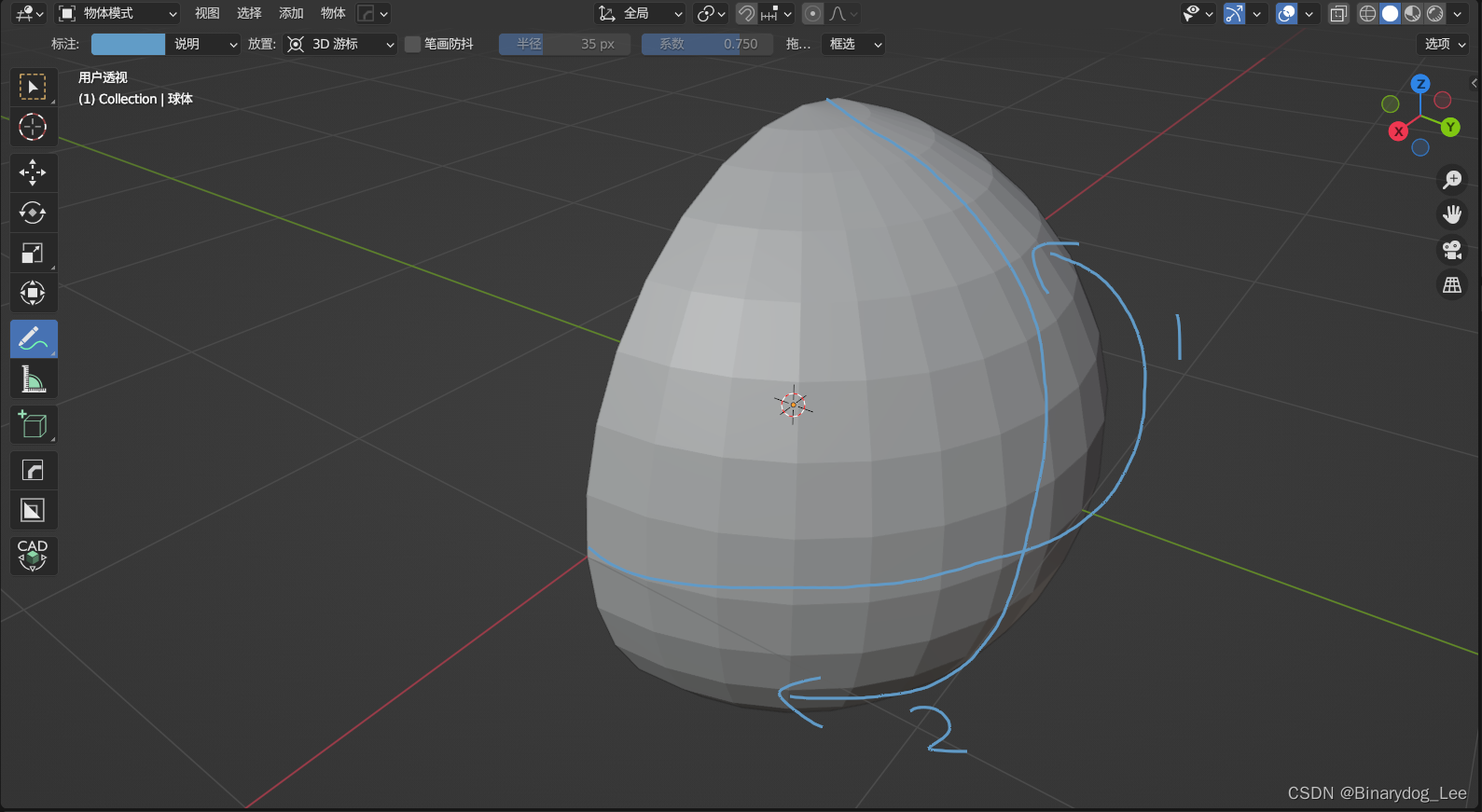
例题

计算三重积分$\underset{\Omega }{\iiint }(x^2+y^2)dv$其中$\Omega$是右半球面$x^2+y^2+z^2=a^2(y\ge 0,a>0)$与$xOz$面所围成的区域

---

【解析】

Ω = { 0 ≤ r ≤ a , 0 ≤ θ ≤ π , 0 ≤ φ ≤ π } \Omega = \{0\le r\le a,0\le \theta \le \pi,0\le \varphi \le \pi \} Ω={0≤r≤a,0≤θ≤π,0≤φ≤π}

本题即解如下积分

$$\underset{\Omega }{\iiint }{r}^2{\sin }^2\phi \cdot r^2\sin \phi drd\theta d\phi$$

即：

$${\int }_0^{\pi }d\theta {\int }_0^{\pi }d\phi {\int }_0^a{r}^4{\sin }^3\phi dr$$

其中在$dr$时${\sin }^3\phi$是常量，可提出，剩下就是对$r^4$积分，即变为：

$${\int }_0^{\pi }d\theta {\int }_0^{\pi }{\sin }^3\phi \cdot \frac{a^5}{5}d\phi$$

$\frac{a^5}{5}$是常数可提出，并且这个对$\phi$积分完要对$\theta$积分，可以先变换顺序先对$\theta$积分，则原式变为：

$$\frac{\pi }{5}{a}^3{\int }_0^{\pi }{\sin }^3\phi d\phi$$

对于${\sin }^3\phi$的积分步骤中用到了点火公式，过程如下：

$${\int }_0^{\pi }{\sin }^3\phi d\phi ={\int }_0^{\frac{\pi }{2}}{\sin }^3\phi d\phi +{\int }_{\frac{\pi }{2}}^{\pi }{\sin }^3\phi d\phi =\frac{2}{3}+{\int }_{\frac{\pi }{2}}^{\pi }{\sin }^3\phi d\phi$$

对于右侧的积分继续进行处理，令$\phi =\pi -t$（好像算是区间再现公式）

$${\int }_{\frac{\pi }{2}}^{\pi }{\sin }^3\phi d\phi ={\int }_{\frac{\pi }{2}}^0{\sin }^3(\pi -t)d(\pi -t)={\int }_{\frac{\pi }{2}}^0{\sin }^3(\pi -t)d(-t)$$

提出负号，上下限颠倒，则右侧积分式等于：

$${\int }_0^{\frac{\pi }{2}}{\sin }^3(\pi -t)dt$$

根据${\sin }^{3}x$的对称性，该式子又等于：

$${\int }_0^{\frac{\pi }{2}}{\sin }^{3}tdt=\frac{2}{3}$$

故原式等于

$$\frac{\pi }{5}{a}^3{\int }_0^{\pi }{\sin }^3\phi d\phi =\frac{\pi }{5}{a}^3\cdot (\frac{2}{3}+\frac{2}{3})=\frac{4}{15}\pi a^5$$

即最终结果