题目描述

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]

• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

解析

这道题最容易想到的解法就是回溯法，通过DFS，将所有的情况都算出来，但是这样算的话，时间复杂度将达到O(n^2)，容易超时。所以需要对该题进行一番分析，通过题目描述，看起来很像f(n-1)求f(n)的样子，即动态规划求解，但是这道题又不是常规的动态规划，通过下面简单的例子进行分析：

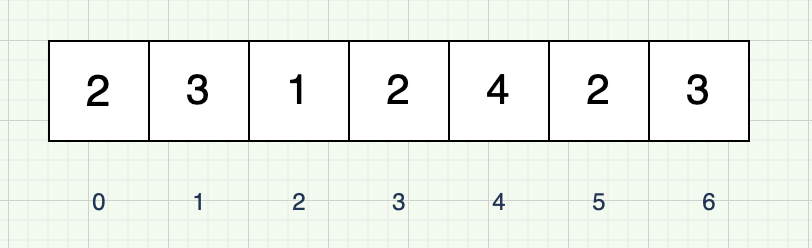
上面是一个长度为7的数组，最少用3步就可以达到末尾：index=[0,1,4]。

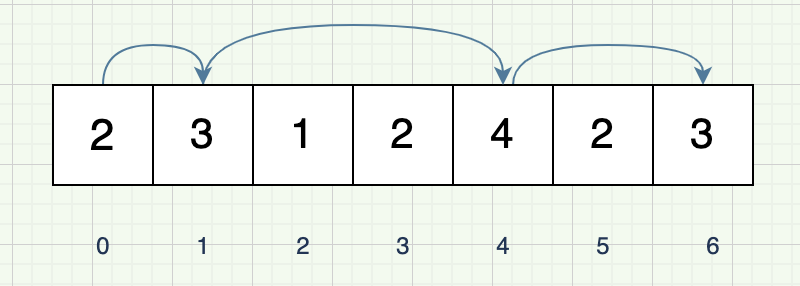
我们可以这样分析，在n步想跳到最远的地方，那么一定是从第n-1步才能够跳到的地方起步的，如下图，如果从index=0开始跳跃的话，绿色部分的两个位置至少跳跃1次才能达到，蓝色部分的两个位置至少要跳跃2次才能达到，红色部分的两个位置至少要跳跃3次才能达到。所以是在前面最优的区段内求下一次能够跳跃到的区段，实际还是动态规划。

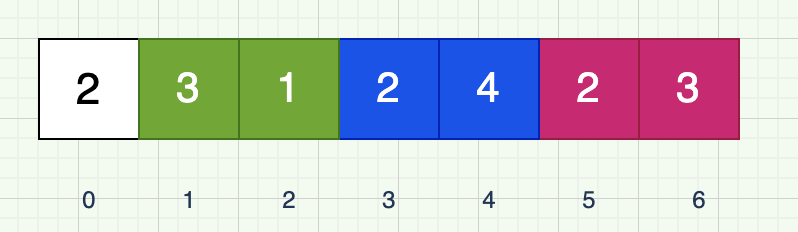
因此，我们可以循环遍历数组，通过临时变量记录当前能够跳跃的最远距离，同时还要记录第N次能够跳跃到的最远的位置，当遍历到这个位置的时候，说明跳跃次数需要加1才能往后面进行。

代码

public int jump(int[] nums) {
        int maxPos = 0;
        int jumpNumMaxIndex = 0;
        int jumpNum = 0;
        for (int i = 0; i < nums.length - 1; i++) {
            maxPos = Math.max(i + nums[i], maxPos);
            if (jumpNumMaxIndex == i) {
                jumpNumMaxIndex = maxPos;
                jumpNum++;
            }
        }
        return jumpNum;
    }