文章目录
- 1、数字特征的定义
- 2、数学期望(均值)
- 2.1、数学期望的定义及性质
- 2.1.1、定义
- 2.1.2、性质
- 2.2、数学期望相关例题
- 2.3、Y=g(X)的数学期望
- 2.4、Z=g(X,Y)的数学期望
- 2.5、随机变量函数的数学期望例题
- 3、方差
- 3.1、方差的定义与性质
- 3.2、相关例题
- 3.3、切比雪夫不等式
- 4、协方差与相关系数
- 4.1、协方差与相关系数的定义
- 4.2、协方差与相关系数的性质
- 4.3、二维正态分布的相关系数
- 5、矩、协方差矩阵
1、数字特征的定义
实际或理论问题中,人们感兴趣的是某些能描述随机变量某一种特征的常数,例如,一个篮球队上场比赛的运动员的身高是一个随机变量,人们常关心的是上场运动员的平均身高;一个城市一户家庭拥有汽车的数是一个随机变量,在考察城市的交通情况时,人们关心的是每户平均拥有汽车的数量;评价棉花的质量时,既需要注意纤维的平均长度,有需要注意纤维长度与平均长度的偏离程度,平均长度较大,偏离程度较小,质量就较好。
由随机变量的分布所确定的,能够刻画随机变量某一方面的特征的常数统称为数字特征。几个重要的数字特征:数学期望,方差,相关系数和矩。
2、数学期望(均值)
2.1、数学期望的定义及性质
2.1.1、定义
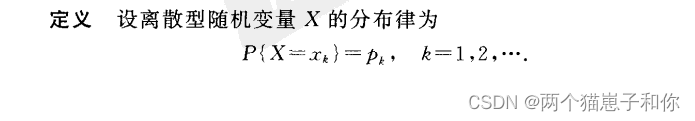

2.1.2、性质


2.2、数学期望相关例题



2.3、Y=g(X)的数学期望

2.4、Z=g(X,Y)的数学期望

2.5、随机变量函数的数学期望例题


3、方差
3.1、方差的定义与性质



3.2、相关例题



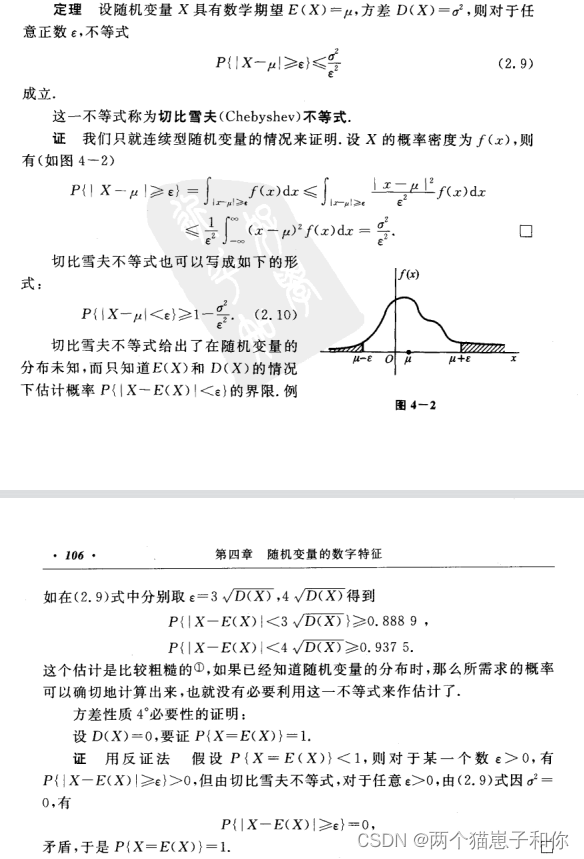
3.3、切比雪夫不等式
4、协方差与相关系数
4.1、协方差与相关系数的定义

4.2、协方差与相关系数的性质


4.3、二维正态分布的相关系数


5、矩、协方差矩阵