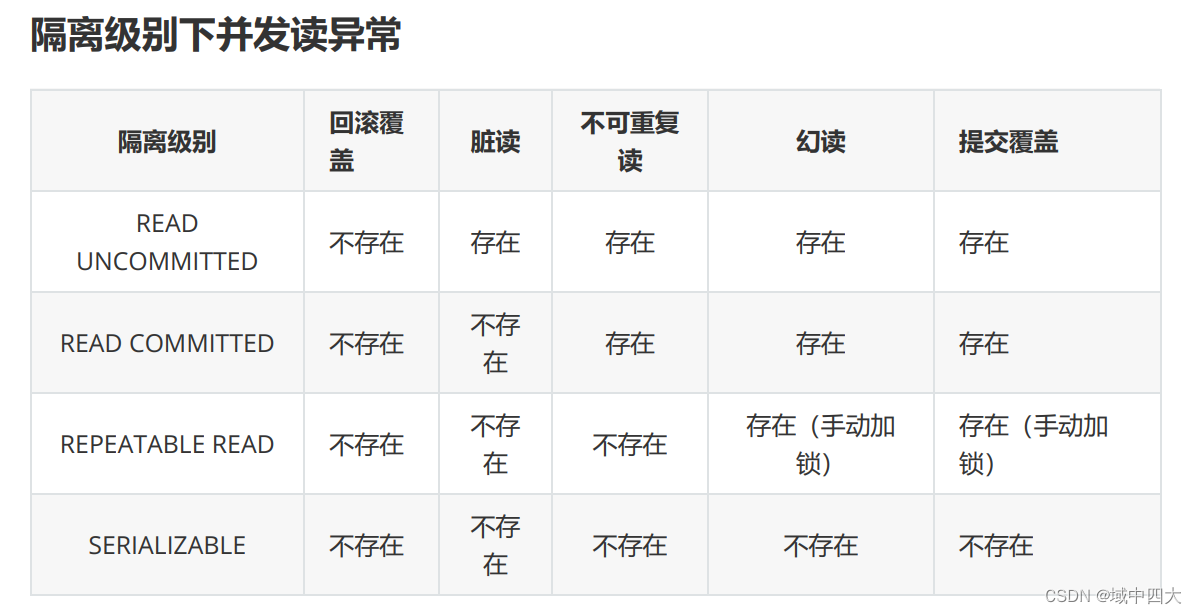
- 文章题目:Adapting Meta Knowledge Graph Information for Multi-Hop Reasoning over Few-Shot Relations
- 时间:2019
摘要
- 多跳知识图 (KG) 推理是一种有效且可解释的方法,用于在查询回答 (QA) 任务中通过推理路径预测目标实体。 大多数以前的方法都假设 KGs 中的每个关系都有足够的训练三元组,而不考虑那些不能为训练鲁棒推理模型提供足够的三元组的小样本关系。 事实上,现有的多跳推理方法在少样本关系上的性能显着下降。 在本文中,我们提出了一种基于元的多跳推理方法(Meta-KGR),它采用元学习从高频关系中学习有效的元参数,可以快速适应少镜头关系。 我们在从 Freebase 和 NELL 采样的两个公共数据集上评估 Meta-KGR,实验结果表明 Meta-KGR 在少镜头场景中优于当前最先进的方法。 我们的代码和数据集可以从 https://github.com/THU-KEG/MetaKGR 获得。
引言
- 最近,大规模知识图谱 (KGs) 已被证明对查询回答 (QA) 等许多 NLP 任务有益。 QA 的三重查询通常形式化为 ( e s , r q , ? ) (e_s, r_q, ?) (es,rq,?),其中 e s e_s es 是源实体, r q r_q rq 是查询关系。 例如,给定一个语言查询“What is the nationality of Mark Twain?”,我们可以将其转化为o (Mark Twain, nationality, ?),然后从 KGs 中搜索目标实体 America 作为答案。 然而,由于许多 KGs 是自动构建的并且面临严重的不完整问题 (Bordes et al., 2013),通常很难直接获得目标实体进行查询。
- 为了缓解这个问题,一些知识图谱嵌入方法 (Bordes et al, 2013; Dettmers et al., 2018) 被提出将实体和关系嵌入到语义空间中以捕获内部连接,然后使用学习到的嵌入进行最终预测。 尽管这些基于嵌入的方法在预测查询的目标实体方面显示出强大的能力,但它们只能给出答案并且缺乏决策的可解释性(Lin 等人,2018)。 为了使模型更直观,Das 等人(2018)和 Lin 等人(2018)提出了多跳推理方法,利用知识图谱中关系的符号组合性来获得可解释的推理结果。 例如,当使用 (Mark Twain, nationality, ?) 查询时,多跳推理模型不仅可以给出目标实体 America,还可以给出多跳可解释路径 (Mark Twain, bornIn, Florida) ∧(Florida, locatedIn, America)。
- 大多数以前的工作都假设有足够的三元组来为知识图谱中的每个关系训练一个有效且稳健的推理模型。然而,如图 1 所示,很大一部分 KG 关系实际上是长尾关系(Xiong et al., 2018; Han et al., 2018)并且只包含很少的三元组,可以称为少样本关系。一些试点实验表明,之前的多跳推理模型,例如 MIN ERVA (Das et al., 2018) 和 MultiHop (Lin et al., 2018),在这些少样本关系上的性能将显着下降。请注意,有一些知识图嵌入模型(Xiong et al., 2018; Shi and Weninger, 2018; Xie et al., 2016)可以处理零样本或单样本关系,但它们仍然有两个主要的缺点:
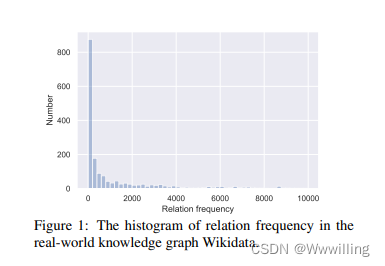
-(1)它们是基于嵌入的模型,缺乏可解释性; (2) 他们关注零镜头或单镜头关系,这与真实世界的场景有些距离。事实上,即使是人,也很难在几乎没有例子的情况下掌握新知识。因此,few-shot multi-hop推理是一个非常重要和实际的问题,但尚未完全解决。
- 在本文中,我们提出了一种基于元的多跳推理算法(Meta-KGR)来解决上述问题,这对于少样本关系是可解释且有效的。 具体来说,在 Meta-KGR 中,我们将 KGs 中具有相同关系 r r r 的三重查询视为一个任务。 对于每项任务,我们采用强化学习 (RL) 来训练代理来搜索目标实体和推理路径。 类似于之前的元学习方法 MAML (Finn et al., 2017),我们使用高频关系任务来捕获元信息,其中包括不同任务之间的共同特征。 然后,通过提供一个良好的起点来训练特定的推理代理,元信息可以快速适应小样本关系的任务。 在实验中,我们在从 Free base 和 NELL 采样的两个数据集上评估 Meta-KGR,实验结果表明 Meta-KGR 在少样本场景中优于当前最先进的多跳推理方法。
问题定义
- 我们正式定义了一个 KG G = { E , R , F } G = \{E, R, F\} G={E,R,F},其中 E E E 和 R R R 分别表示实体和关系集。 F = { ( e s , r , e o ) } ⊆ E × R × E F = \{(e_s, r, e_o)\} ⊆ E × R × E F={(es,r,eo)}⊆E×R×E 是三元组,其中 e s , e o ∈ E e_s, e_o ∈ E es,eo∈E 是实体, r ∈ R r ∈ R r∈R 是它们之间的关系。 在本文中,如果提及关系 r r r 的三元组数量小于特定阈值 K K K,则认为 r r r 为少镜头关系,否则为正常关系。
- 给定一个查询 ( e s , r q , ? ) (e_s, r_q, ?) (es,rq,?),其中 e s e_s es 是源实体, r q r_q rq 是少样本关系,少样本多跳推理的目标是为该查询预测正确的实体 e o e_o eo。 与之前的知识图谱嵌入工作不同,多跳推理还给出了一条从 e s e_s es 到 e o e_o eo 到 G G G 的推理路径来说明整个推理过程。
相关工作
- Knowledge Graph Embedding (Bordes et al., 2013; Yang et al., 2015; Dettmers et al., 2018) 旨在将实体和关系嵌入到低维空间中,然后使用嵌入来定义得分函数 f ( e s , r , e o ) f(e_s, r, e_o) f(es,r,eo) 来评估三元组为真的概率。 最近,几个模型(Xie 等人,2016 年;Shi 和 Weninger,2018 年)结合了额外的实体描述来学习未见实体的嵌入,这可以看作是零样本场景。 Xiong 等人 (2018) 在具有挑战性的环境下预测新事实,其中对于给定关系 r r r 只有一个训练三元组可用,这可以看作是一次性场景。 尽管这些模型很有效,但它们的决策缺乏可解释性。
- KG 上的多跳推理旨在从 G 中的关系路径中学习符号推理规则,近年来已被表述为顺序决策问题。 DeepPath(Xiong 等人,2017 年)首先将 RL 应用于给定查询的知识图谱中搜索推理路径,这在后来的工作中发挥了重要作用(例如,MINERVA(Das 等人,2018 年)和 DIVA(Chen 等人., 2018)).由于很难训练 RL 模型,Reinforce Walk (Shen et al., 2018) 提出使用 off-policy 学习来解决奖励稀疏性问题。 MultiHop (Lin et al., 2018) 通过奖励整形和动作丢失进一步扩展了 MIN ERVA,实现了最先进的性能。这些推理方法直观且可解释。但是,它们在少镜头场景中的表现都较差。除了 KGs 的 multi-hop reasoning 之外,近年来也出现了一些 multi-hop QA 方法。 Yang et al (2018) 提出了一个高质量的数据集,极大地促进了该领域的发展。之后,许多方法如 CogQA (Ding et al., 2019) 和
还提出了 DFGN (Xiao et al., 2019)。 - 元学习试图解决“快速适应新训练任务”的问题。 它已被证明在少样本任务上非常成功(Lake et al., 2015; Gu et al., 2018)。 以前的元学习模型主要集中在计算机视觉和模仿学习领域。 在本文中,我们提出了一种使用元学习算法 MAML(Finn 等人,2017)进行少样本多跳推理的新模型(Meta-KGR)。 据我们所知,这项工作是针对多跳推理的少数样本学习的第一项研究。
模型
- MAML 的主要思想是使用一组任务为具有少量训练示例的新任务学习良好初始化的参数
θ
∗
θ∗
θ∗。 当应用于少样本多跳推理时,具有相同关系
r
r
r 的三重查询被视为任务
T
r
T_r
Tr。 我们使用具有正态关系的三元组来找到初始化良好的参数
θ
∗
θ∗
θ∗ 并根据找到的初始参数在具有少样本关系的三元组上训练新模型。 如图 2 所示,我们可以轻松快速地适应具有参数
θ
r
1
θ_{r_1}
θr1、
θ
r
2
θ_{r_2}
θr2 或
θ
r
3
θ_{r_3}
θr3 的新模型,用于小样本关系
r
1
r_1
r1、
r
2
r_2
r2 或
r
3
r_3
r3。
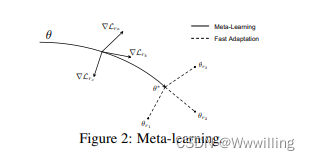
- Meta-KGR的学习框架可以分为两部分:(1)relation-specific learning; (2) 元学习。 Relation-specific learning 旨在为特定关系 r r r(任务)学习一个带有参数 θ r θ_r θr 的 REINFORCE 模型,以搜索目标实体和推理路径。 元学习基于特定关系学习,用于学习具有参数 θ ∗ θ∗ θ∗ 的元模型。 我们将在接下来的章节中介绍这两个部分。
4.1 Relation-Specific Learning
- 对于每个查询关系 rq ∈ R,我们学习了一个特定于关系的多跳推理代理来搜索 G 上的推理路径和目标实体,这是基于 Lin 等人(2018)提出的 on-policy RL 方法。
4.1.1 强化学习公式
- 对 G G G 的搜索过程可以看作是一个马尔可夫决策过程 (MDP):我们将 G G G 表示为一个有向图,实体和关系分别为节点和边。 当给定一个查询及其答案 ( e s , r q , e o ) (e_s, r_q, e_o) (es,rq,eo) 时,我们期望 r q r_q rq 的代理可以从源实体 e s e_s es 开始并通过几条边到达目标实体 e o e_o eo。 更具体地,MDP定义如下。
- 状态:第 t t t个时间步的状态被定义为一个元组 s t = ( r q , e s , e ^ t ) s_t = (r_q, e_s, \hat e_t) st=(rq,es,e^t),其中 r q r_q rq是查询关系, e s e_s es是源实体, e ^ t \hat e_ t e^t是当前G上的实体。
- 动作: 给定状态 s t s_t st的动作空间 A t A_t At包括 e ^ t \hat e_t e^t的所有出线边和下一个实体。 A t = { ( r t + 1 , e ^ t + 1 ) ∣ ( e ^ t , r t + 1 , e ^ t + 1 ) ∈ G } A_t= \{(r_{t + 1}, \hat e_{t + 1}) |(\hat e_t,r_{t + 1}, \hat e_{t + 1})∈G\} At={(rt+1,e^t+1)∣(e^t,rt+1,e^t+1)∈G}。我们为每个 A t A_t At添加一条自循环边,这类似于“STOP”动作。
- 转换:对于状态 s t s_t st,如果代理选择一个动作 ( r t + 1 , e ^ t + 1 ) ∈ A t (r_{t+1},\hat e_{t+1})∈A_t (rt+1,e^t+1)∈At,则状态将变为 s t + 1 = ( r q , e s , e ^ t + 1 s_{t+1} = (r_q, e_s, \hat e_{t+1} st+1=(rq,es,e^t+1)。转换函数定义为 δ ( s t , A t ) = ( r q , e s , e ^ t + 1 δ(s_t, A_t) = (r_q, e_s, \hat e_{t+1} δ(st,At)=(rq,es,e^t+1)。在本文中,我们将搜索在 G G G上展开到固定的时间步数 T T T,最终得到状态 s T = ( r q , e s , e ^ T s_T = (r_q, e_s, \hat e_T sT=(rq,es,e^T)。
- 奖励:如果智能体最终停在正确的实体,即 e ^ T = e o \hat e_T = e_o e^T=eo,则奖励 R ( s T ∣ r q , e s ) R(s_T |r_q, e_s) R(sT∣rq,es)将为1,否则它将获得基于嵌入的奖励 f ( e s , r q , e ^ T ) f(e_s, r_q, \hat e_T) f(es,rq,e^T),其中 f f f是来自知识图嵌入方法的评分函数,用于测量 ( e s , r q , e ^ T ) (e_s, r_q, \hat e_T) (es,rq,e^T)的概率。
4.1.2 策略网络
- 为了解决上述MDP问题,我们需要一个在每个状态下都有策略选择行动的模型。具体而言,与一般的RL问题不同,我们应用了一个考虑
G
G
G上搜索历史的策略网络,形式上,在
G
G
G中分别嵌入所有实体和关系
e
∈
R
d
e∈R^d
e∈Rd和
r
∈
R
d
r∈R^d
r∈Rd后,
a
t
=
(
r
t
+
1
,
e
^
t
+
1
)
∈
A
t
a_t = (r_{t+1}, \hat e_{t+1})∈A_t
at=(rt+1,e^t+1)∈At的每个动作表示为
a
t
=
[
r
t
+
1
;
e
^
t
+
1
]
a_t = [r_{t+1}; \hat e_{t+1}]
at=[rt+1;e^t+1]。我们使用LSTM来编码搜索路径。
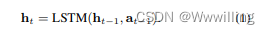
- 然后,我们通过将
A
t
A_t
At中的所有动作叠加为
A
t
∈
R
∣
A
t
∣
×
2
d
A_t∈R^{|A_t|×2d}
At∈R∣At∣×2d来表示动作空间。参数化的策略网络定义为
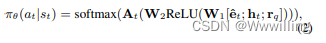
- 其中 π θ ( a t ∣ s t ) π_θ(a_t|s_t) πθ(at∣st)是 a t a_t at中所有作用的概率分布。
4.1.3 损失函数
- 给定一个查询关系
r
r
r和一批集合为
D
D
D的三元组,且具有关系
r
r
r,则该关系的总体损失定义为:
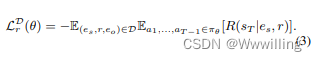
4.2 元学习
- 在元学习中,我们的目标是学习初始化良好的参数 θ ∗ θ * θ∗,这样,参数的微小变化将对任何任务的损失函数产生显著的改进(Finn et al., 2017)。
- 形式上,我们考虑一个参数为
θ
θ
θ的元策略网络。当适应新的任务
T
r
T_r
Tr时,模型的参数变为
θ
r
′
θ'_r
θr′。对于MAML,更新后的参数
θ
r
′
θ'_r
θr′是使用任务
T
r
T_r
Tr上的一个或多个梯度下降更新计算的。例如,假设以学习率
α
α
α采取一个梯度步骤
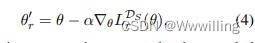
- 在掌握了关系相关参数
θ
r
′
θ'_r
θr′之后,我们在属于
T
r
T_r
Tr的查询集DQ上计算
θ
r
′
θ'_r
θr′,该查询集像DS一样采样。通过计算得到的梯度可以用来更新具有参数
θ
θ
θ的元策略网络。通常,我们会在一批中检查许多任务,并将
θ
θ
θ更新为下面的内容:
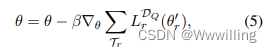
- 其中
β
β
β为元学习率。我们在算法1中详细介绍了元学习算法。

- 在经过前面的元学习步骤之后,通过使用 θ θ θ作为初始化良好的参数 θ ∗ θ * θ∗, Meta-KGR可以快速适应于每个少数镜头关系的特定关系策略网络。
实验
5.1 数据集
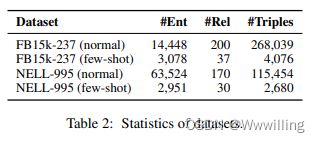
- 我们使用FB15K-237 (Toutanova et al., 2015)和NELL-995 (Xiong et al., 2017)两个典型数据集进行训练和评估。具体来说,我们设置K = 137和K = 114分别从FB15K-237和NELL995中选取少量镜头关系。此外,我们重建了NELL-995,以生成有效集和测试集的few-shot关系。表2中分别给出了正常关系和少数镜头关系的统计数据。
基线
- 我们在实验中比较了四种多跳推理模型:(1)神经逻辑编程(NerualLP) (Yang et al., 2017);(2) NTP-λ (Rocktaschel and Riedel¨,2017);(3) MINERVA (Das等人,2018)和(4)MultiHop (Lin等人,2018)。对于MultiHop和我们的模型,我们使用DistMult (Yang et al., 2015)和ConvE (Dettmers et al., 2018)作为奖励函数来创建两种不同的模型变体,在表1的括号中标记了它们。
链接预测
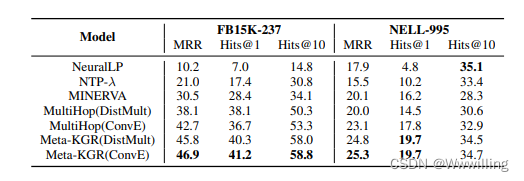
- 给定一个查询 ( e s , r q , ? ) (e_s, r_q, ?) (es,rq,?), QA的链接预测旨在从KG中给出候选实体的排序列表。继之前的工作(Dettmers等人,2018;Lin et al., 2018),我们在该任务中使用了两个评估指标:(1)所有正确实体的平均倒数排名(MRR)和(2)排名不大于N的正确实体的亲校对部分(Hits@N)。
- 两个数据集的评价结果如表1所示。从表中我们可以得出:(1)我们的模型在大多数情况下优于以往的工作,这意味着从高频关系中学习到的元参数可以很好地适应少炮关系。(2)在模型中,ConvE作为奖励函数优于DistMult。这表明更有效的知识边图嵌入方法可以为训练多跳推理模型提供更细粒度的奖励。(3)与NELL-995相比,FB15K237密度更大。我们的模型在两个数据集上都表现良好,这表明Meta-KGR可以适应不同类型的KGs。
鲁棒性分析
- 我们可以用不同的频率阈值 K K K来选择少炮关系。在本节中,我们将研究K对我们模型性能的影响。在我们的实验中,一些三元组将被删除,直到每几个镜头的关系只有K个三元组。我们在FB15K-237上做了链路预测实验,并使用ConvE作为我们的奖励函数。最终结果如表3所示。K = max意味着我们使用表2中的整个数据集,并且不删除任何三元组。从表3中我们可以看到我们的模型对K是健壮的,并且在任何情况下都优于MultiHop。
结论
- 本文提出了一种基于元学习的知识图少镜头关系多跳推理模型Meta-KGR。Meta-KGR使用具有高频关系的训练三元组来查找初始化良好的参数值,并快速适应少镜头关系。从高频关系中得到的元信息对少炮关系有帮助。在实验中,我们的模型在少数镜头关系上取得了良好的性能,在大多数情况下优于以往的工作。一些实证分析也表明,我们的模型是稳健的,并可推广到不同类型的知识图。