---

前言

这篇文章是集合排序的知识,十分详细,可作为复习资料。我们需要掌握的排序方法有七种，分别是堆排序，快速排序，冒泡排序，选择排序，希尔排序，直接插入排序,归并排序。下面我们分别讲述这些排序的原理和应用。大家一定要对照着里面的图进行学习,不难的,我们开始啦!

---

1. 直接插入排序

1.1 画图演示

原数组,我们来具体说明怎么排序这个数组吧~

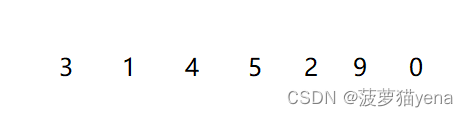
如下图，先排第二个元素1,定义循环变量（i=1),定义tmp等于arr[i]，前面的3大于tmp,把3向后挪,==arr[j+1] = arr[j] ,j- -,==之后发现前面没有元素了(j < 0),退出循环,元素1就排好了

之后i++，排第三个元素4,前面的元素比它小,即（arr[j] ＜tmp）符合条件,退出循环,4排好了

i++，排第四个元素5,5同样,前面的4比它小,已经是有序的了

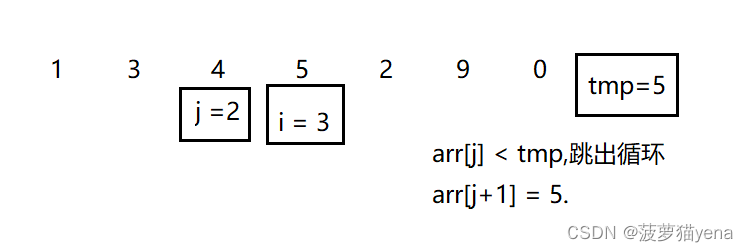
之后，i++，排第五个元素2,如下图,前面元素5,arr[j] > tmp, 把5往后挪(arr[j+1] = arr[j])
之后j-- ,再看4,4也是比2大,把4向后挪
直到当(j = 0)时,arr[j]是1,1比2小,就把2放在1的后面,也就是arr[j+1] = tmp

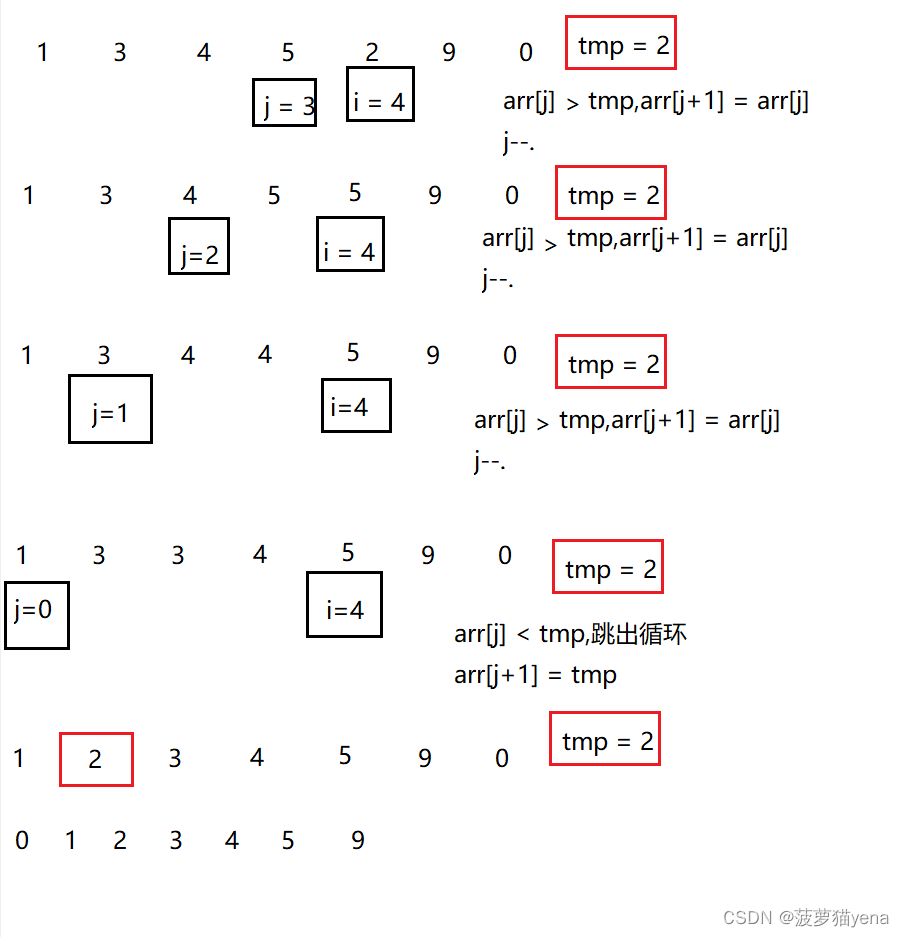
最后的9,0 一样的操作，不做赘述。最后排好的数组

1.2 直接插入排序详细步骤

1. 排序一个数组，从数组第二个元素开始，与前面的元素比较。
2. 先用变量tmp把这个元素存起来，如果前面的元素比它大，就把前面的元素向后挪，直到前面的元素比它小或者前面已经没有元素的时候，就把元素放在这个位置，这个元素就排完了。
3. 为每个元素找到自己正确的位置，直到排完最后一个元素，数组就有序了。
4. 举例。如下图，排序如下数组。

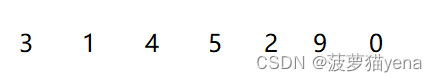
先排第二个元素1，先用变量tmp把元素1存起来，与前面的元素比较，发现1比3小，将3向后挪一位，用arr[j+1] = arr[j]来实现向后挪的动作.

因为从第二个元素到最后一个元素的每个元素都得找合适的位置，所以外层循环开始条件是第二个元素（i = 1），结束条件是最后一个元素（i < arr.length）。

那什么时候算是排好一个元素呢，就是前面元素比它小，或者前面已经没有元素了。所以内层循环的初始条件是从i的前一个元素开始比较(j = i - 1),结束条件是发现前面已经没有元素了（j >= 0）.当（arr[j] < tmp）就代表找到对应的位置可以跳出循环了。把存好的tmp放到arr[j]后面的位置上。

public static void insertSort(int[] arr){
        for(int i = 1; i < arr.length; i++){
            int tmp = arr[i];
            int j = i - 1;//注意这里因为跳出内层循环时要使用j的位置，所以要把j定义在外循环中。
            for(; j >= 0; j--){
                if(arr[j] > tmp){
                    //前面元素大，把元素向后挪
                    arr[j+1] = arr[j];
                }else{
                    //前面的元素比tmp小，意味着找到正确位置，跳出循环
                    break;
                }
                //把arr[j]后面的位置给tmp.如果j = -1,
                //说明tmp就是前面的最小的元素，那就把arr[0]给tmp
            }
            arr[j+1] = tmp;
        }
    }

1.3 时间复杂度，空间复杂度分析

下面的链接,是具体介绍怎么计算时间复杂度和空间复杂度的.
https://editor.csdn.net/md/?articleId=126723532
直接插入排序适合数组趋于有序的时候,数组有序，直接插入排序时间复杂度能达到O(1).在==数组逆序的时候,时间复杂度达到最高,==为(n-1)+(n-2)+(n-3)+…+1,等差数列求和.
直接插入排序未占用额外空间.
时间复杂度：O(N^2)
空间复杂度: O(1)

2. 希尔排序

希尔排序是直接插入排序的优化,是怎么优化的呢?我们在直接插入排序中说过,当数据趋于有序时,是非常适合直接插入排序的.

2.1 具体步骤描述

这个方法需要画图辅助,才能清楚描述
排序如下数组

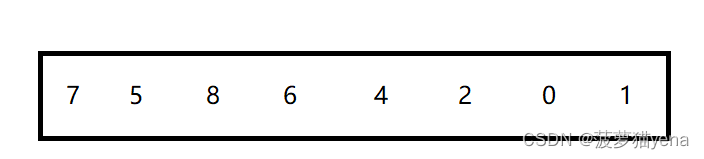
将数组分组排序,先定义gap = arr.length/2, 将所有相隔gap的数组元素进行排序,如图
arr[4]与arr[0]比较,arr[0]>arr[4],交换位置,把较小的换到前面,arr[5]arr[1]比较,arr[1]>arr[5],交换位置,以此类推,直到最后一个元素.

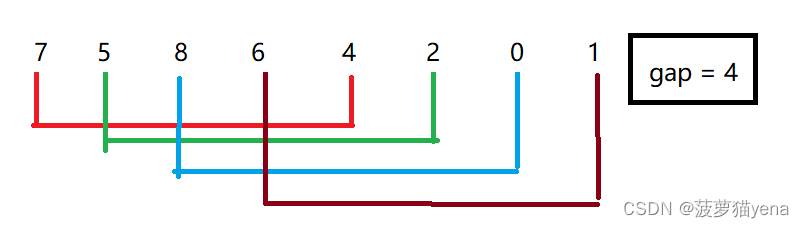
执行交换位置之后得到下图

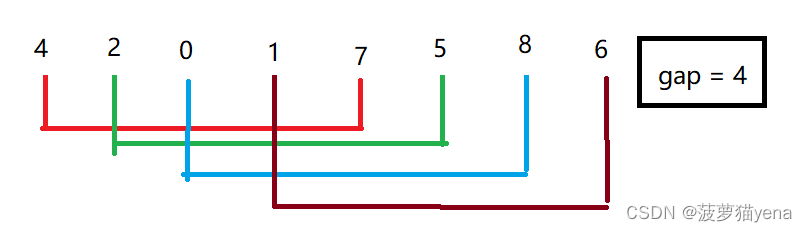
令gap = gap/2,之后,令所有间隔为2的元素进行比较.把较小的往前换.如下图

执行完交换操作之后得到下图

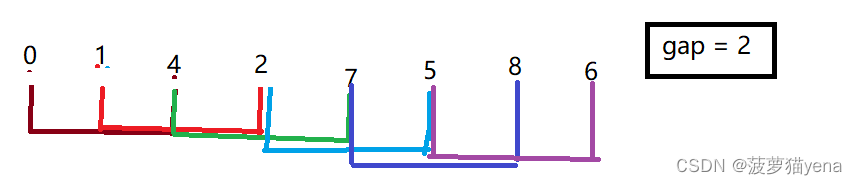
之后再gap = gap/1, gap = 1,这时,排序就成了直接插入排序,由于数据已经趋于有序,所以排序的速度非常快.由于整个排序的过程,数据一直是逐渐趋于有序,所以==整个过程,排序速度是越来越快的.==最后得到如下数组

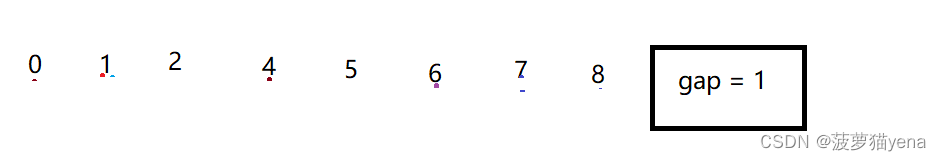
2.2 代码详解

如下代码,希尔排序的代码和直接插入的代码极其相似,就是在直接插入排序排序代码的基础上改动了几个地方.
i从gap处开始,依次与arr[i-gap]比较大小把较小值换到前面.,之后i++,直到i = arr.lengrh-1.

public static void shellSort(int[] arr){
        int gap = arr.length;
        while(gap >= 1){
            for(int i = gap; i < arr.length; i++){
                int tmp = arr[i];
                int j = i - gap;
                for(; j >= 0; j-= gap){   //注意这里,是j -= gap, 不是j--
                    if(arr[j] > tmp){
                    //注意这里是j+gap
                        arr[j+gap] = arr[j];
                    }else{
                        break;
                    }
                }
                arr[j+gap] = tmp;
            }
            gap /= 2;
        }
    }

2.3时间复杂度,空间复杂度分析

时间复杂度: O(n^2)
空间复杂度: O(1)
大家可能会有疑惑,为什么时间复杂度都是O(n^2)却把希尔排序称作直接插入排序的优化呢?
因为希尔排序,是逐渐把数组变得有序,每次排序的速度是越来越快的.
我们实操一下,获取语句执行时间的代码是

long start = System.currentTimeMillIs();

{执行语句};

long end = System.currentTimeMillIs();
 System.out.println("执行语句的执行时间为"+(end - start));

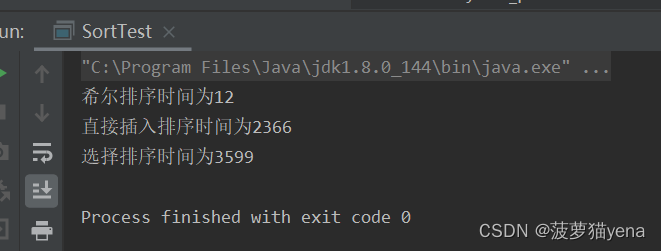
下图是,排序同一个数组,数组元素设为100000个逆序数据时,直接插入排序和希尔排序执行时间的差别,可以看出,希尔排序是比直接插入排序优秀的.

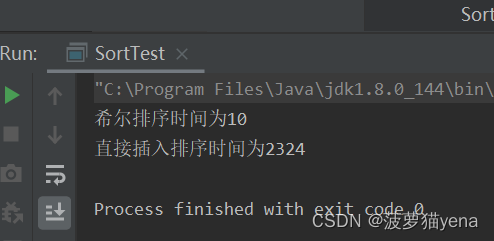
当是100000个趋于有序的数据时,两方法时间,直接插入排序更适合.所以,直接插入排序非常适合趋于有序的数组

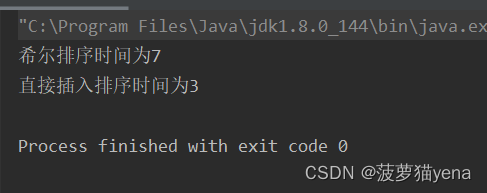
3. 选择排序

选择排序,简单易懂.是从已有的数据中,选出最小的依次往后放,放完整个数组,数组就是有序的了.这个排序可以进行优化.我们这里直接介绍优化后的选择排序.优化呢,也很简单,就是==挑最小的和最大的,把最小的放前面,把最大的放后面.==两头抓,更快点.

3.1 画图讲解

如下图,找到数组最小值和最大值,最小值==min与arr[0]交换,最大值max与arr[length-1]==交换,

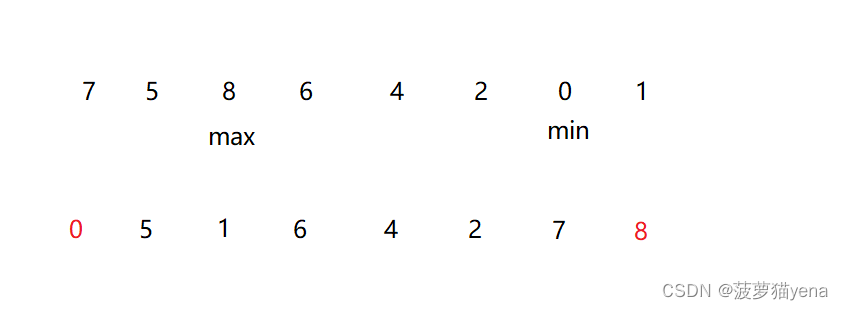
之后再从未排序数据中找出最大值最小值,再分别与前后元素交换,如下图

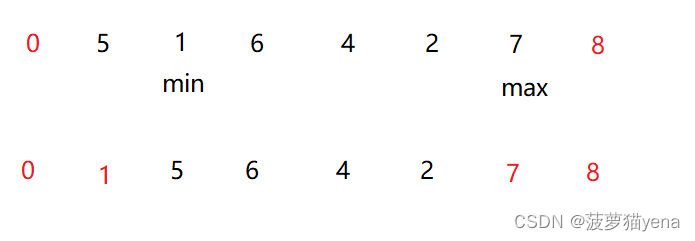
以此类推,在未排好序的数组中找出最小值,与前面元素交换,找出最大值,与后面元素交换
后续操作如下

3.2 代码讲解

用left,right控制排序进度,left起始值为0,right起始值为arr.length-1,每次排好一组数,left++,right–当left >= right排序结束.
注意一个易错点,当maxIndex == left时,前面经过swap(arr,minIndex,left);后,arr[left]的值已经被换到minIndex位置.
可以参考下图,maxIndex 等于 left时,经过swap(arr,minIndex,left);后5已经被换到了minIndex位置,所以要maxIndex = minIndex;来调整maxIndex的位置

public static void selectSort(int[] arr){
        long start = System.currentTimeMillis();
        int left = 0;
        int right = arr.length-1;
        while(left < right){
            int minIndex = left;
            int maxIndex = right;
            for(int i = left; i <= right; i++){
                if(arr[i] < arr[minIndex]){
                    minIndex = i;
                }else if(arr[i] > arr[maxIndex]){
                    maxIndex = i;
                }
            }
            swap(arr,minIndex,left);
            if(maxIndex == left){
                maxIndex = minIndex;
            }
            swap(arr,maxIndex,right);
            left++;
            right--;
        }
        long end = System.currentTimeMillis();
        System.out.println("选择排序时间为"+(end - start));
    }

    public static void swap(int[] arr, int a, int b){
        int tmp = arr[a];
        arr[a] = arr[b];
        arr[b] = tmp;
    }

3.3 时间复杂度,空间复杂度分析

时间复杂度: O(n^2)
空间复杂度: O(1)
100000个逆序数据,三种方法时间比较

4. 快速排序

快速排序,顾名思义,速度快.

4.1 画图演示

基本实现方法是,先以首元素arr[0]为基准,先从末尾向前找比arr[0]小的元素right,再从arr[1]开始,找到比arr[0]大的元素left,令left下标元素与right下标元素交换.

如下图,先从右向左找到比arr[0]小的元素1,再从左向右找比arr[0]大的元素5,令1和5交换

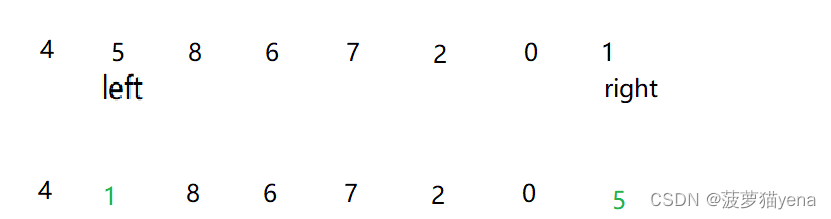
之后,right继续向左找到小于arr[0]的元素0,left向右找大于arr[0]的元素8,0和8交换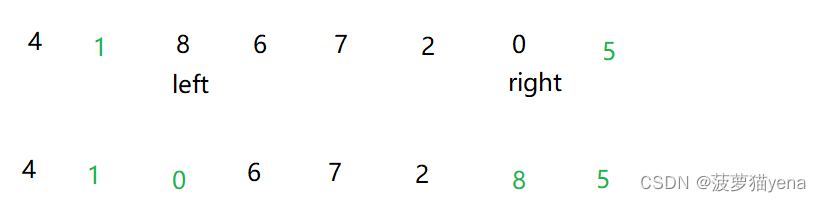
以此类推,直到left与right相遇,循环结束,交换arr[0]和相遇的元素值,第一次排序就正式结束了.

观察上图,我们会发现,基准4的左边元素都比他小,4右边的元素都比他大.所以,我们只需对4左右的元素分成两组,分别排序后,数组就是有序的.

由于排序过程都是一样的,所以分别对基准左右元素排序的操作,我们用递归实现.
不同的是,左边的元素,从arr[0]开始到基准前的元素结束.
右边的元素从基准后的元素开始,到数组末尾结束.

用同样的方法对左边元素进行排序,把2当做新排序的基准,排2的左小组,再以0为基准,排0的右小组

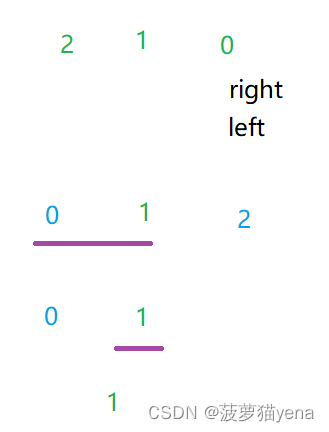
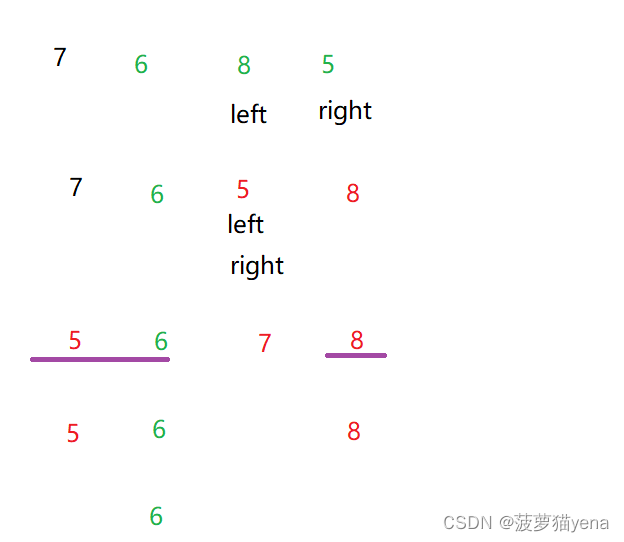
对右边元素进行排序,把7当做新排序的基准,排7的左小组5和6, 7的右小组8,再以5为基准,排5的右小组6

4.2 代码详解

先进行第一次排序.
用(left < right)控制循环结束条件,先在右侧找到小于基准的,再在左侧找到大于基准的,交换数值后,继续循环.
需要注意的点
由于最后要交换arr[left]和left与right相遇处的值,所以,事先要定义一个index记录下来left的位置,int index = left;

 public static int partition(int[] arr, int left, int right){
        int tmp = arr[left];
        int index = left;
        while(left < right){
            while(right > left && arr[right] >= tmp){
                right--;
            }
            while(right > left && arr[left] <= tmp){
                left++;
            }
            swap(arr, left, right);
        }
        swap(arr,index, left);
        return left;
    }

由于,还要分别排序基准的左小组和右小组,更换基准,所以,我们会用到递归.那递归体和递归结束的条件怎么找呢.
我们先考虑怎么写这个递归,每次都要分别排序基准的左小组和右小组,每次分组的开始和结束位置都不同,如下图.左小组的开始位置没动,结束位置变成相遇处-1,右小组的开始位置变成相遇处+1,结束位置没变.

如下代码,用pivot记录上次相遇的坐标,那么左小组的排序就是开始位置与上次排序的结束位置相同,结束位置变成pivot-1,quick(arr, start, pivot-1);右小组的排序是开始位置是pivot+1,结束位置与上次排序的结束位置相同

 	public static void quick(int[] arr, int start, int end){
        int pivot = partition(arr, start, end);
        quick(arr, start, pivot-1);
        quick(arr, pivot+1, end);
    }

那怎么找递归的结束条件呢,我们来看什么情况下,递归会结束.如下图,当左小组只剩一个元素时,end = pivot -1,end < start,这时,只有一个元素,无需排序,就可以结束递归了.

右小组只剩一个元素时,start = pivot + 1,此时,start>end,递归结束

综上,递归结束的条件是==(start > end)==
所以,递归结束语句为

if(start > end){
	return;
}

快速排序完整代码如下

public static void quick(int[] arr, int start, int end){
        if(start >= end){
            return;
        }
        int pivot = partition(arr, start, end);
        quick(arr, start, pivot-1);
        quick(arr, pivot+1, end);
    }

    public static int partition(int[] arr, int left, int right){
        int tmp = arr[left];
        int index = left;
        while(left < right){
            while(right > left && arr[right] >= tmp){
                right--;
            }
            while(right > left && arr[left] <= tmp){
                left++;
            }
            swap(arr, left, right);
        }
        swap(arr,index, left);
        return left;
    }

4.3 时间复杂度,空间复杂度分析

由于使用了递归会占据内存的栈区,所以快速排序的空间复杂度是O(logN),是递归的次数
时间复杂度是O(n^2)
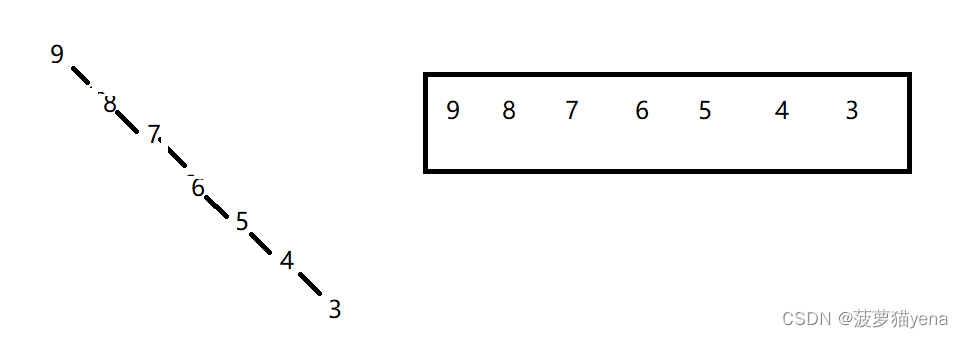
要注意一种特殊情况,当要排序的数组是逆序时,或者顺序的时候,例如9876543,我们看到,递归的次数变成了n,空间复杂度达到了O(n).所以,我们得出,当数组趋向有序的时候,不适合使用快速排序.

4.5 快速排序的优化–挖坑法

4.5.1 画图详解

为了解决快速排序不适合有序序列的问题,我们设计挖坑法对快速排序进行优化.
挖坑法的实现原理与快速排序类似,也不难.
如图,排序如下数组

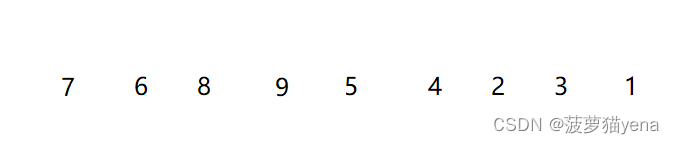
还是,先以arr[0]为基准,先定义tmp存储基准的值,把arr[0]挖走,如图

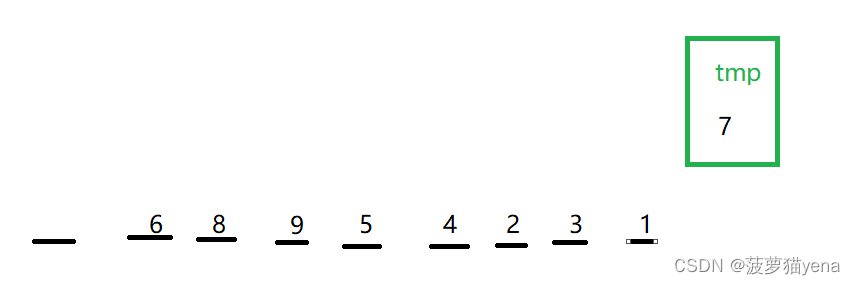
先定义right为arr[length-1],从right位置向前找,找小于tmp的元素1,把1挖出来,填到arr[0]位置,如下图

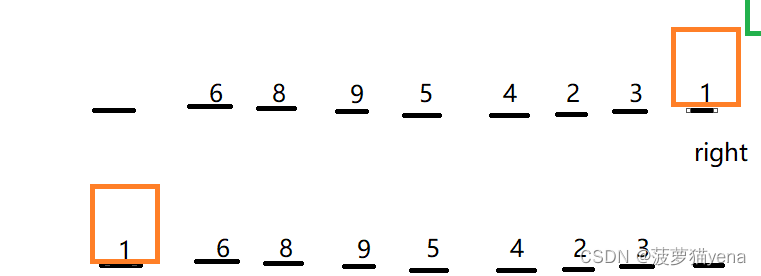
再定义left为0,从left向右找大于基准的,找到了6,把6挖出来,填到右面的坑里

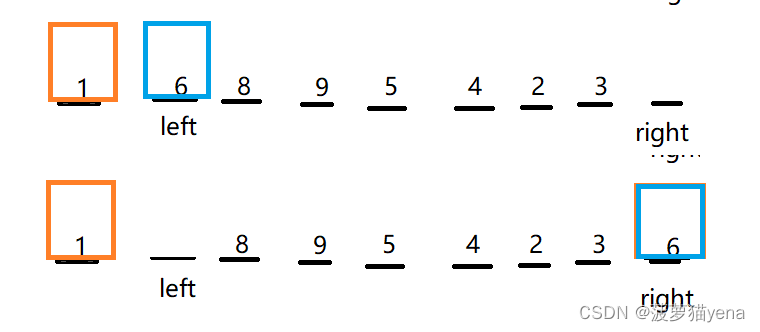
之后,再right往左找小于基准的,挖走,放到左边的坑里.left往右找大于基准的放到右边的坑里.

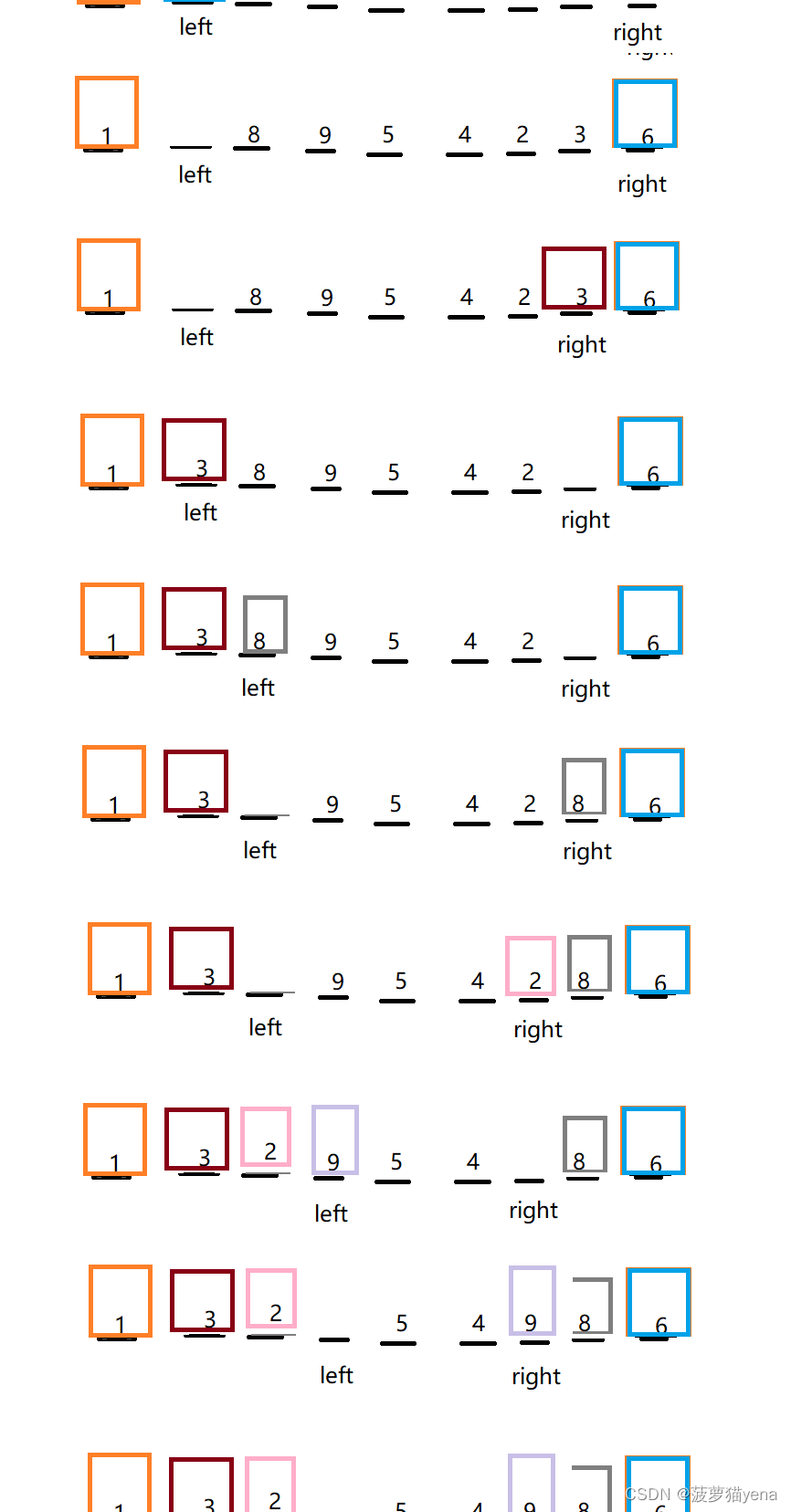
直到right,left相遇,把tmp放在left,right相遇的位置,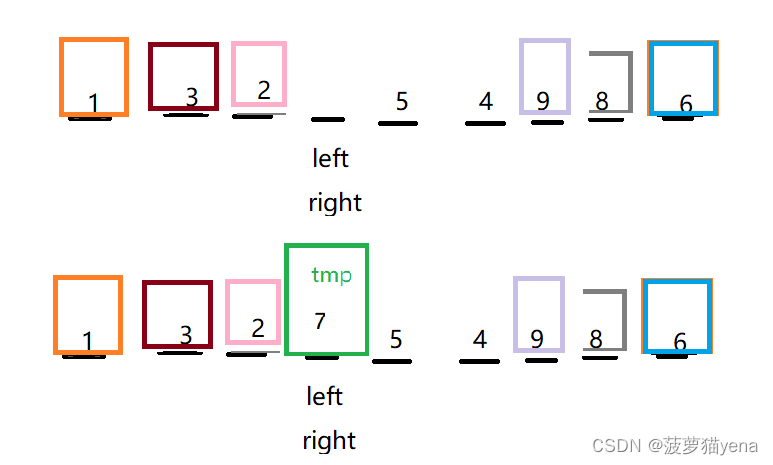
这时,我们发现,tmp左边元素的值都小于它,tmp右边元素的值都大于它.之后,再和快速排序一样,分别以相同的步骤递归tmp的左小组和右小组,递归条件不变.

4.5.2 代码详解

递归的初始和终止条件与快速方法一致.
不同的地方是,找到比基准小的right,找到比基准大的left,快速排序是要进行交换.而挖坑法是直接赋值

		while(right > left && arr[right] >= tmp){
                right--;
            }
            //找到right,把right挖走,放到left坑里
            arr[left] = arr[right];
            while(right > left && arr[left] <= tmp){
                left++;
            }
            把找到的left挖走,放到right坑里
            arr[right] = arr[left];
        }

完整代码如下

public static int[] quickSort02(int[] arr){
        quick02(arr,0,arr.length-1);
        return arr;
    }

    public static void quick02(int[] arr, int start, int end){
        if(start > end){
            return;
        }
        int pivot = partition02(arr, start, end);
        quick02(arr, start, pivot-1);
        quick02(arr, pivot+1, end);
    }

    public static int partition02(int[] arr, int left, int right){
        int tmp = arr[left];
        while(left < right){
            while(right > left && arr[right] >= tmp){
                right--;
            }
            arr[left] = arr[right];
            while(right > left && arr[left] <= tmp){
                left++;
            }
            arr[right] = arr[left];
        }
        arr[left] = tmp;
        return left;
    }

5. 冒泡排序

5.1 排序讲解

冒泡排序,是我们刚接触C语言时,就会学到的排序,我们需要牢记的是,两次循环的循环条件.假如要排十个数,外层9次循环就可以,内层第一次循环是9次,第二次循环是8次,所以内层循环控制条件是==(j < arr.length -1 - i)==

5.2 代码演示

public static void bubbleSort(int[] array){
        for(int i = 0; i < array.length-1; i++){
            for(int j = 0; j < array.length -1 - i; j++){
                if(array[j] > array[j+1]){
                    swap(array,j,j+1);
                }
            }
        }
    }

5.3 时间复杂度,空间复杂度分析

时间复杂度:O(N^2)
空间复杂度:O(1)

6. 归并排序

6.1 排序原理讲解

归并排序,顾名思义呢,是先递归,再合并,不难.它是怎么递归,又是怎么合并的呢?例如排序如下数组

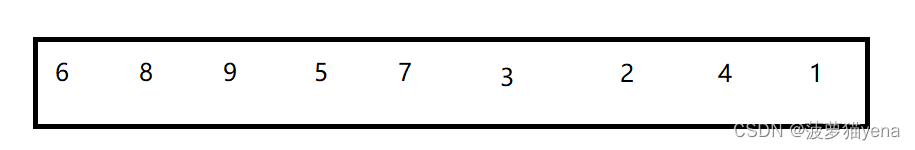
首先呢,先拆数组.找到数组的中间位置mid,将数组分为左右两部分,左半部分是left到mid,右半部分是mid+1到right.如下图

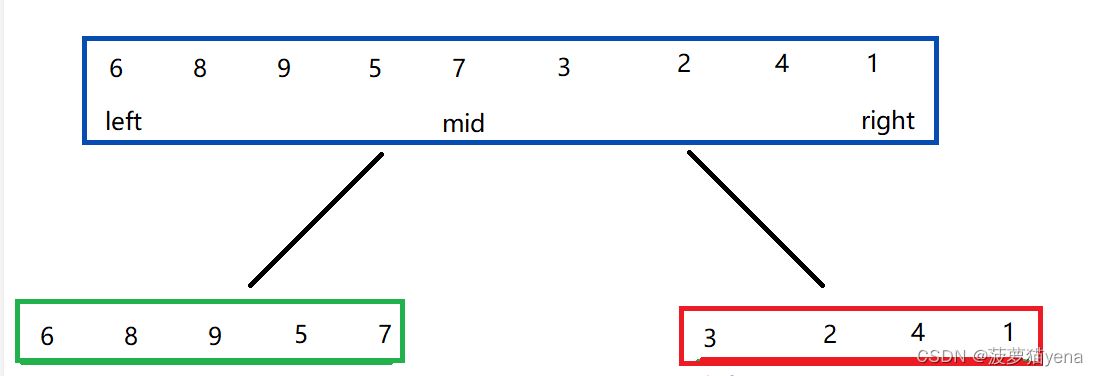
再重新确定left,right,mid,再次拆数组,直到只剩一个元素的时候,例如下图,这是拆右面的数组.可以很清晰的看到,递归的截止条件是(left == right)

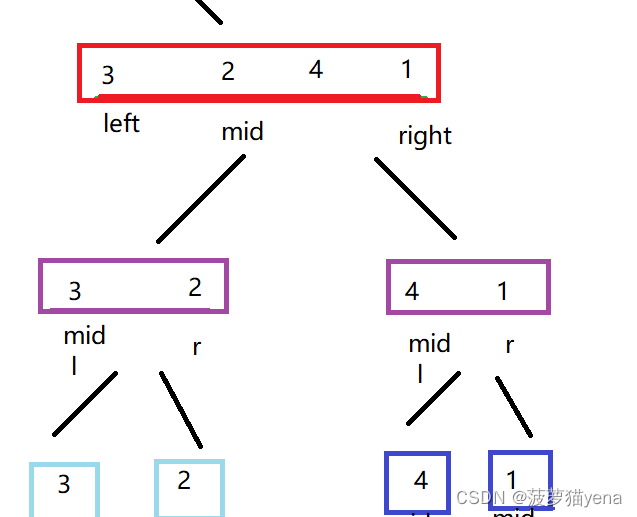
拆完之后,就开始合并数组啦,怎么合并呢?我们来继续看.
我们合并的核心思想就是合并两个有序数组,使合并后的数组仍然有序.

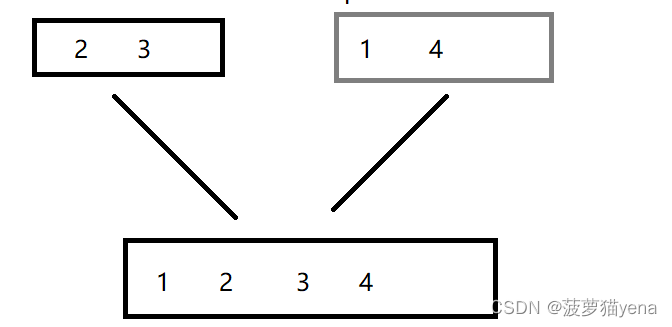
1. 先分别合并3,2,使其成为一个有序数组,合并4,1,使其成为一个有序数组.如下图
2. 
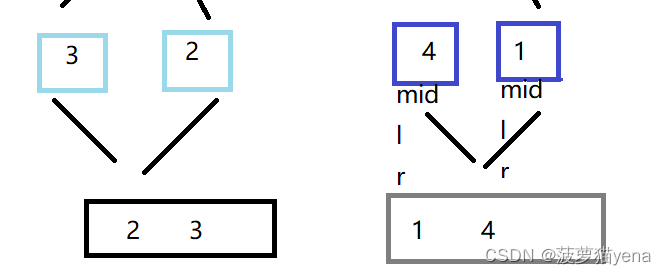
   再合并23与14数组,使其成为一个有序数组,如下图
   
   左小组也是一样,先拆,再合并,如下图
   
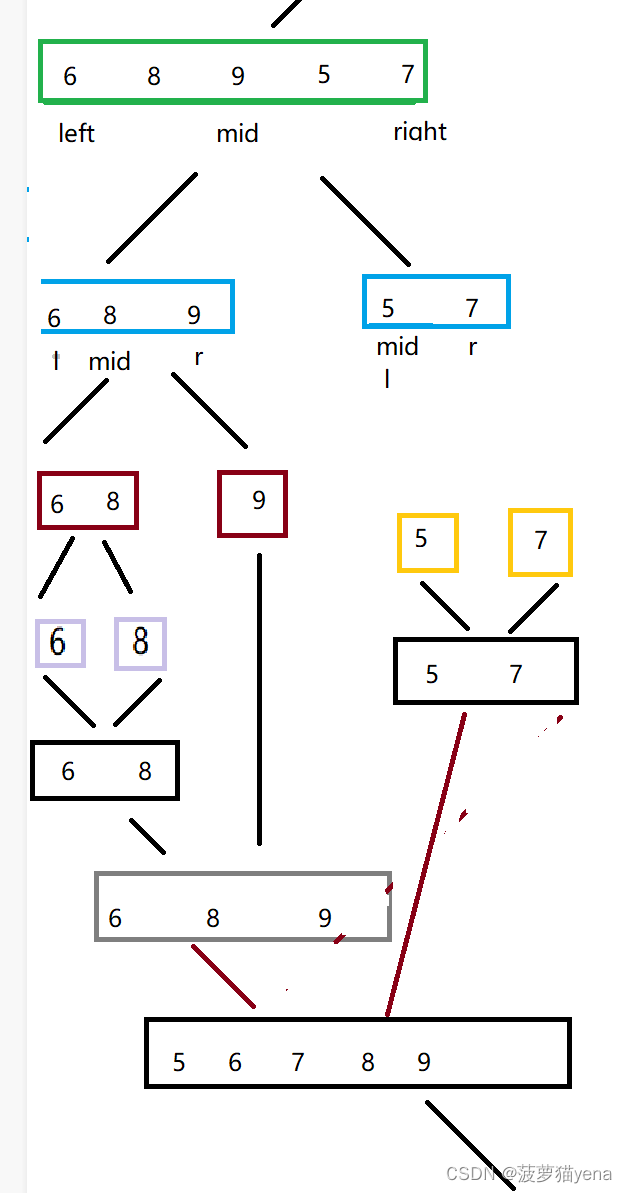
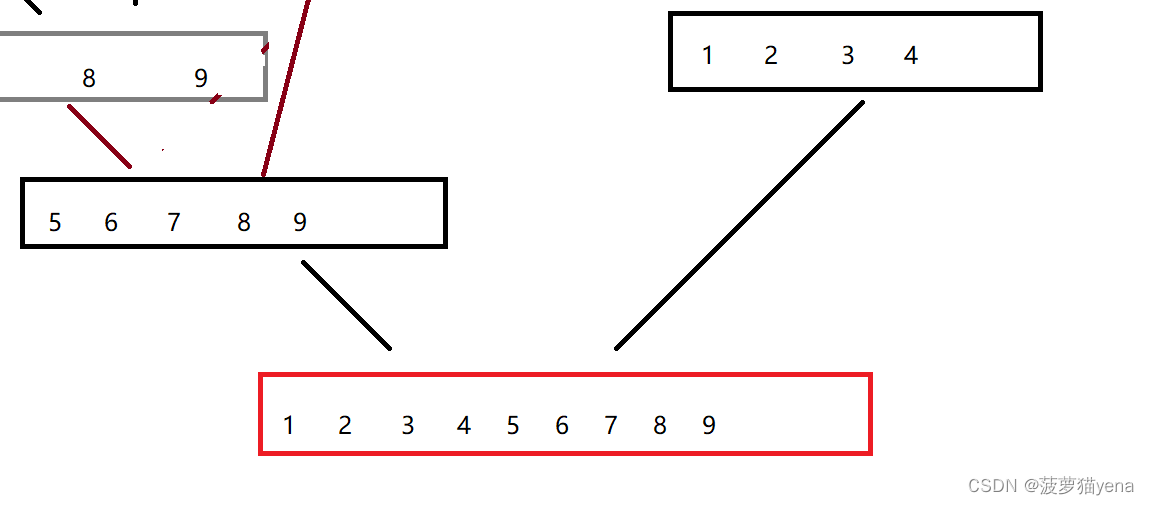
   最后,在合并两个大数组,使其称为有序数组,这个数组就排序完成了.
   

6.2 代码详解

首先,我们要明确每次分组时,每组的起止位置.左小组的left不变,right变成mid,右小组的right不变,left变成mid+1.如下图所示.

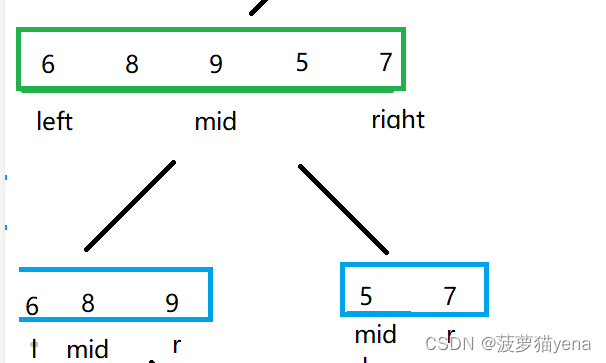
所以递归我们这么写

public static void mergeChild(int[] arr, int left, int right){
        if(left == right){
            return;
        }
        int mid = (left+right)/2;
        mergeChild(arr,left,mid);
        mergeChild(arr, mid+1, right);
        merge(arr,left,mid,mid+1,right);
    }

然后,怎么合并两个有序数组呢,如下图,tmp是新数组,用于容纳最后排好序的数组.注意新数组的长度(right-left+1)
注意这里,由于最后要用到s1的初始值,所以要定义index记录一下s1.代码的最后一句话好好看一下.

private static void merge(int[] arr, int s1, int e1, int s2, int e2){
        int index = s1;
        int[] tmp = new int[e2-s1+1];//合并后数组的新长度(尾-首+1)
        int k = 0;
        while(s1 <= e1 && s2 <= e2){
            if(arr[s1] <= arr[s2]){
                tmp[k++] = arr[s1++];
            }else{
                tmp[k++] = arr[s2++];
            }
        }
        while(s1 <= e1){
            tmp[k++] = arr[s1++];
        }
        while(s2 <= e2){
            tmp[k++] = arr[s2++];
        }
        for(int i = 0; i < k; i++){
            //注意这里,由于最后要用到s1的初始值,所以要定义index记录一下
            arr[i+index] = tmp[i];
        }
    }

完整代码如下

	public static int[] mergeSort(int[] arr){
        mergeChild(arr,0,arr.length-1);
        return arr;
    }

    public static void mergeChild(int[] arr, int left, int right){
        if(left == right){
            return;
        }
        int mid = (left+right)/2;
        mergeChild(arr,left,mid);
        mergeChild(arr, mid+1, right);
        merge(arr,left,mid,mid+1,right);
    }

    private static void merge(int[] arr, int s1, int e1, int s2, int e2){
        int index = s1;
        int[] tmp = new int[e2-s1+1];//合并后数组的新长度(尾-首+1)
        int k = 0;
        while(s1 <= e1 && s2 <= e2){
            if(arr[s1] <= arr[s2]){
                tmp[k++] = arr[s1++];
            }else{
                tmp[k++] = arr[s2++];
            }
        }
        while(s1 <= e1){
            tmp[k++] = arr[s1++];
        }
        while(s2 <= e2){
            tmp[k++] = arr[s2++];
        }
        for(int i = 0; i < k; i++){
            //注意这里,由于最后要用到s1的初始值,所以要定义index记录一下
            arr[i+index] = tmp[i];
        }
    }

6.3 时间复杂度,空间复杂度分析

使用了递归,空间复杂度为O(N)
时间复杂度为O(n*logn)

7. 堆排序

7.1 排序原理

堆排序使用到完全二叉树这个数据结构,那我们来复习一下会用到的关于树的相关知识吧.
如下图,是一颗普通的树
根节点：没有前驱结点的结点,就是它前面没有别的结点了.
下图的根结点有两个孩子,左边的叫左孩子,右边的叫右孩子.
左孩子又作为父亲节点,有左右两个孩子.
每个结点都有自己的值(下面会展示,这个图没写结点的值)

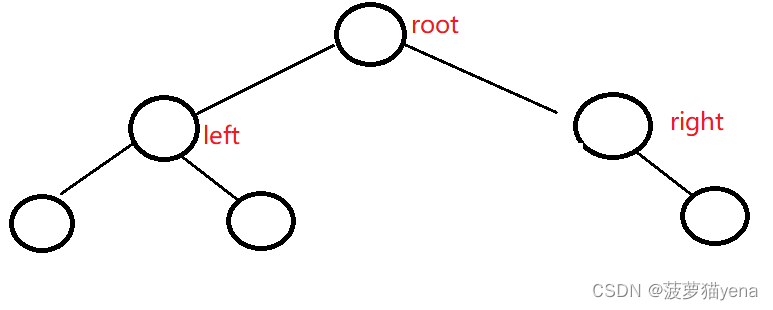
完全二叉树
下面这棵树是完全二叉树,完全二叉树就是树必须从左到右按顺序,中间不能有空的地方,上面那棵树由于最后一棵子树空出了左孩子,所以不是完全二叉树.

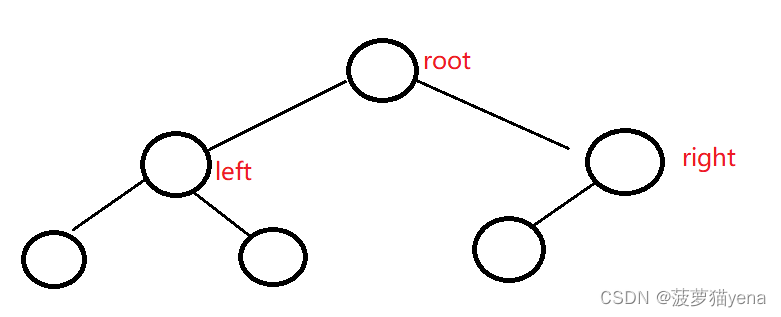
大根堆
大根堆是每一个父亲结点都要大于它的左右孩子的值,如下图

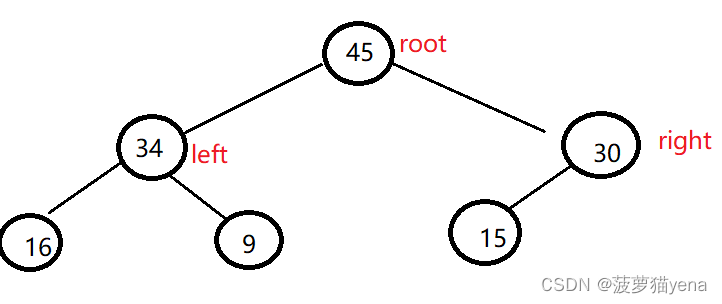
小根堆就是所有的父亲结点的值都要小于左右孩子.
为结点标下标的话,我们会发现一些规律,从根为0下标开始,设父亲结点坐标为i,它的左孩子下标为2 x i+1,右孩子的坐标为2 x i+2.,那么设孩子结点下标为t时,父亲结点为(t-1)/2.

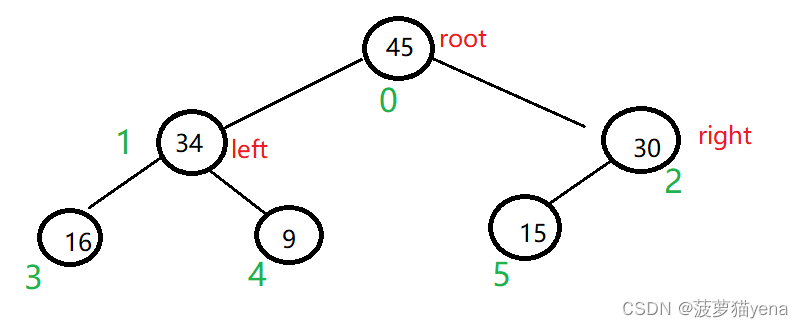
我们是怎么利用这棵树排序数组的呢?

1. 我们先根据要排序的数组数据,建一个大根堆.
   那么根节点的值就是数组的最大值
2. 把根节点放到树的末尾,数组的最大值就排好了.
3. 之后再把其余结点调整为大根堆,那么根节点就是其余节点的最大值.
4. 再把这个节点放到末尾.
5. 这样循环,调整完所有结点,这个树从上到下,从左到右就是有序的了

7.2 画图讲解

1.先要建一个大根堆,这个要怎么建堆呢?我们往下看.
先从最后一棵树开始向下调整,使每棵树的父亲结点的值大于左右孩子结点的值.
怎么实现这个操作呢,就是先在左右孩子结点找出较大的值,与父亲结点值比较,若是父亲结点值较小,就将父亲结点值与这个孩子节点值交换.
如图,看最后一棵树,父亲结点值28,小于左孩子结点值37,交换父亲结点值与左孩子结点值,需要注意,我们这里说的树的顺序是从上到下,从左到右的.

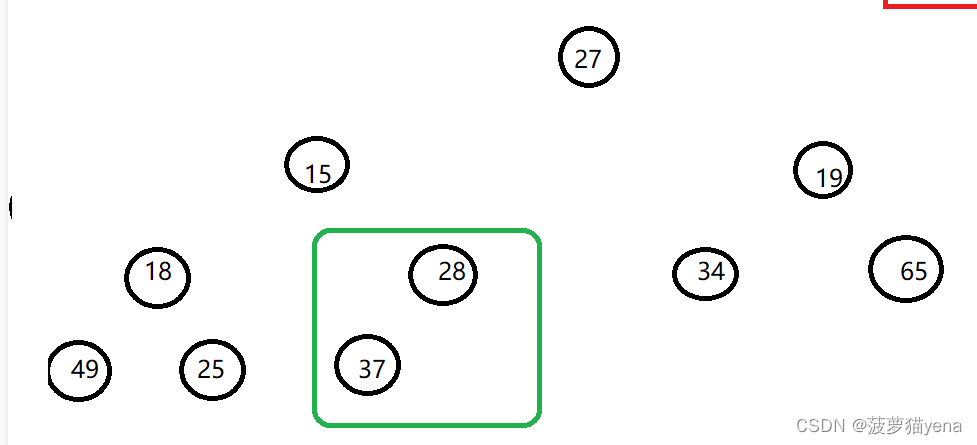
交换后如下图,最后一棵树就调整好了

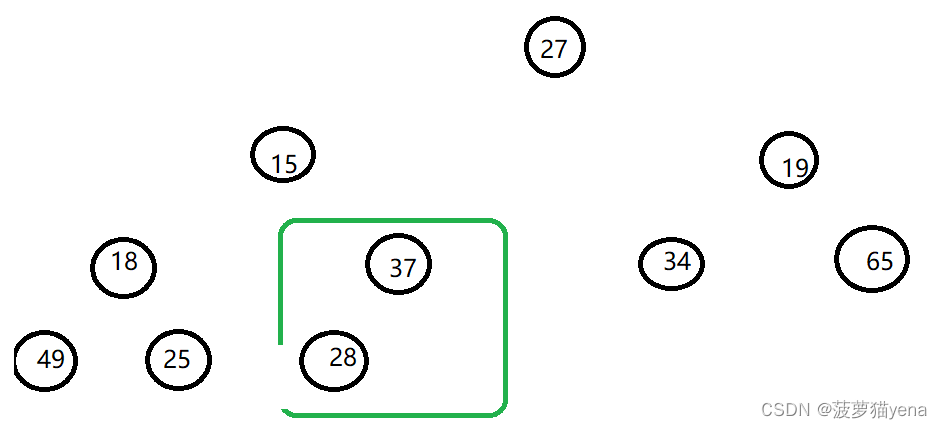
之后,按照同样的方法再从倒数第二棵树开始向下调整.如下图,找出这棵树左右孩子的较大值左孩子49,与父亲结点18比较,大于父亲节点的值,交换父亲结点值和左孩子结点值

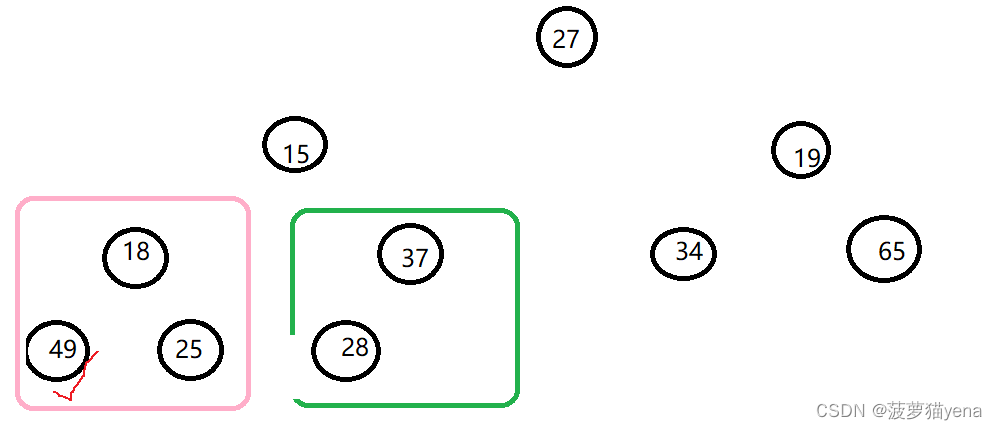
交换后,如下图

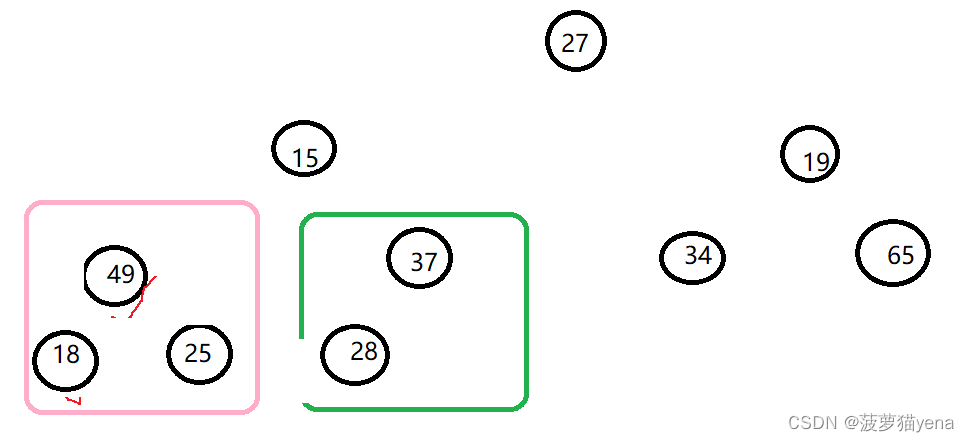
再往前一棵树调整,找出左右孩子较大值65,比父亲结点19大,交换

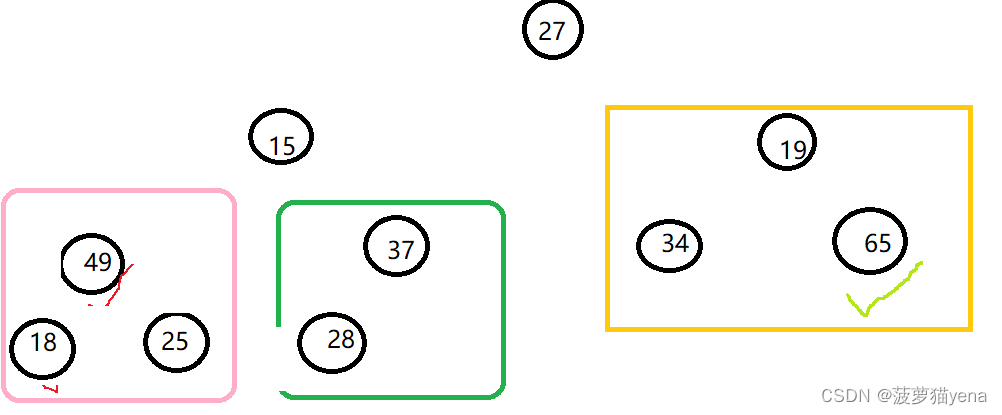
交换后如图

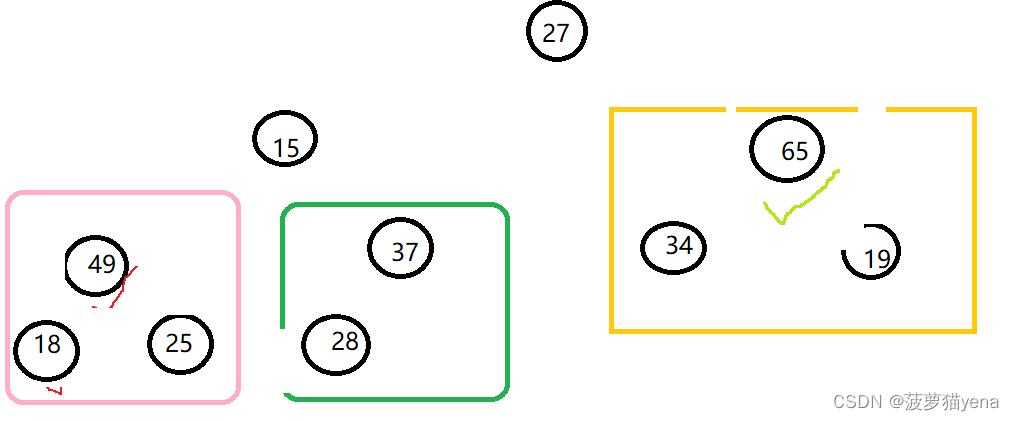
再往前调整,找出左右孩子较大值49,比父亲结点15大,交换

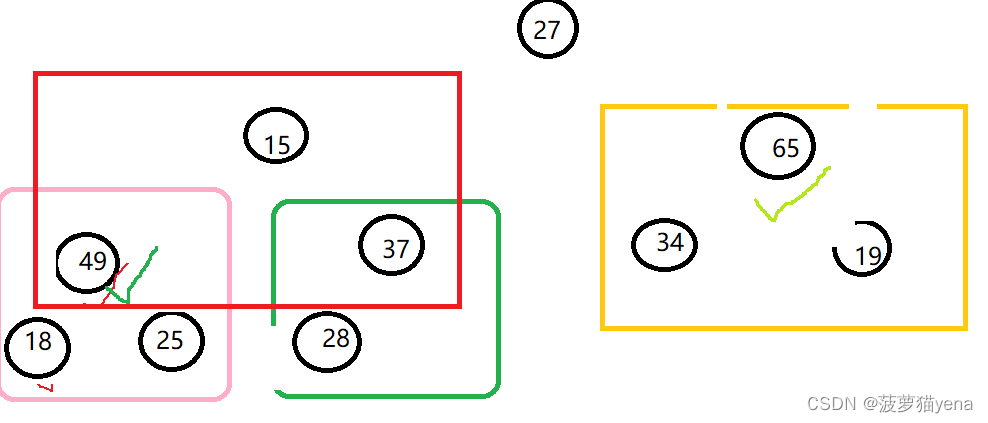
交换后如图,这是我们发现下面调整好的的树也被影响了.父亲结点为15的那棵树,它的父亲结点值比左右孩子的值都小,所以,要把这棵树调整一下,令父亲结点值15与右孩子值25交换.

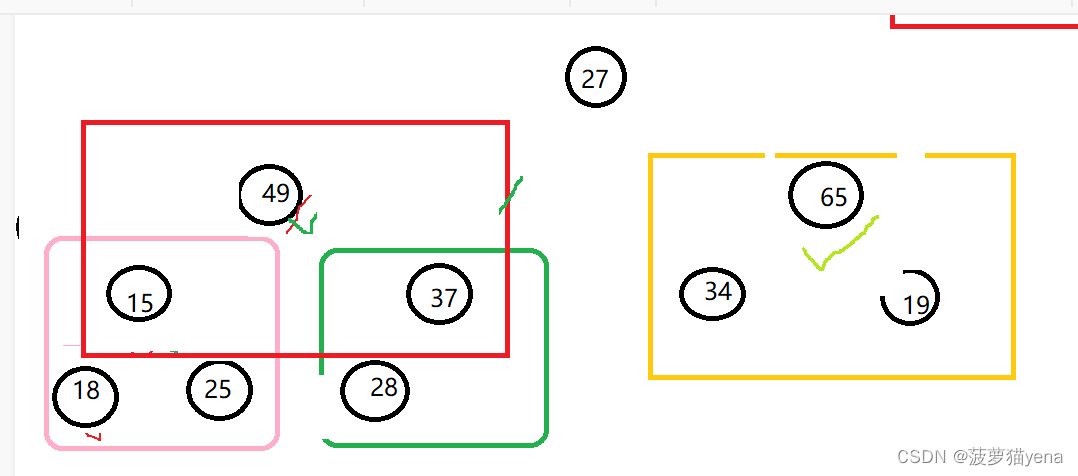
交换后如下图

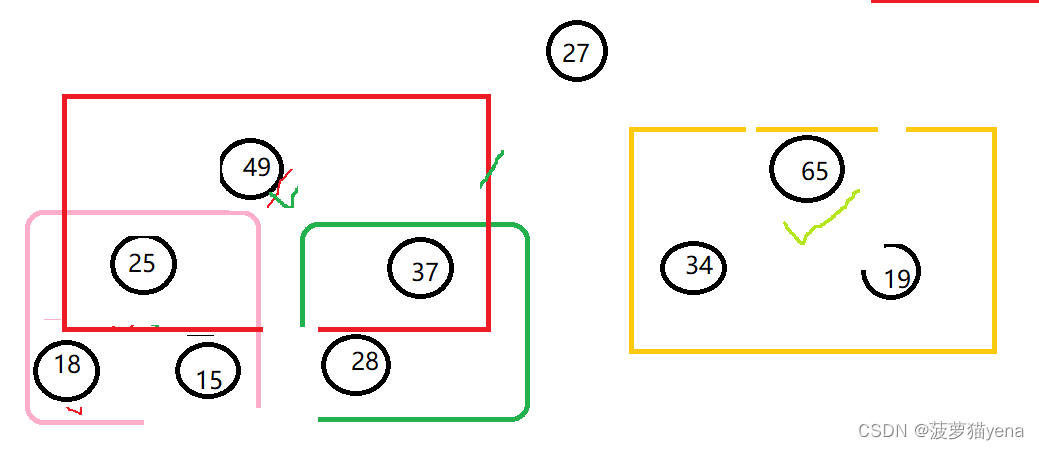
再调整前面的树.同样的套路,这里不再赘述.

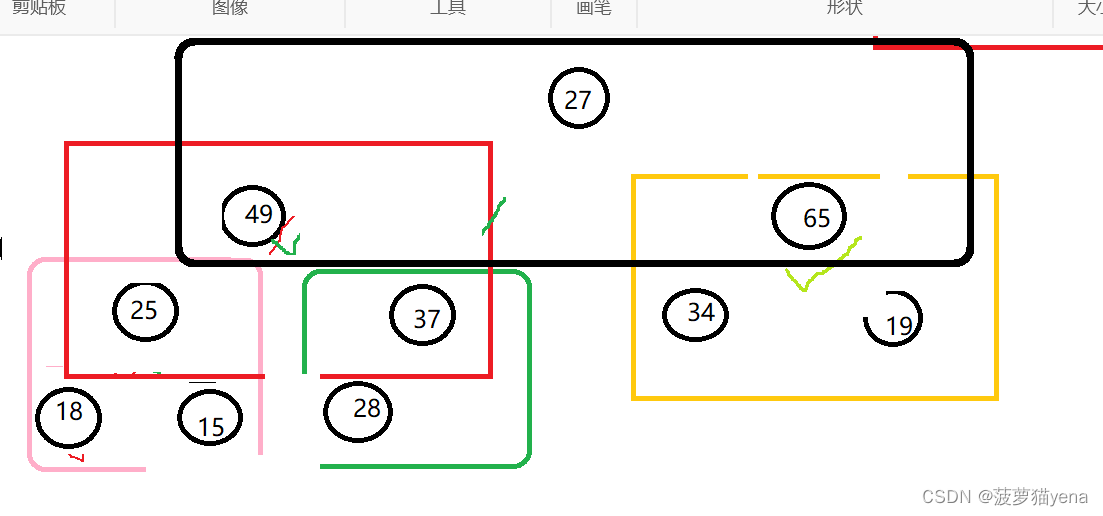
大家自己试着调整一下,调整好的树如下图所示.这个就是最终的大根堆了.我们看到,每一棵子树,它的父亲结点的值都要大于左右孩子节点的值.而根节点65是所有节点中最大的值.

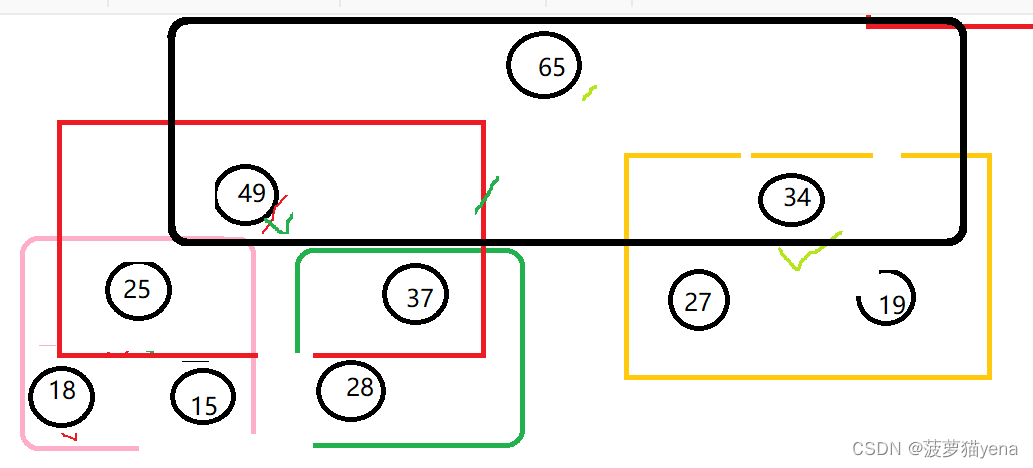
还没完哦,之后把根节点值与末尾值交换,这样,就把最大值换到最后了.如下图

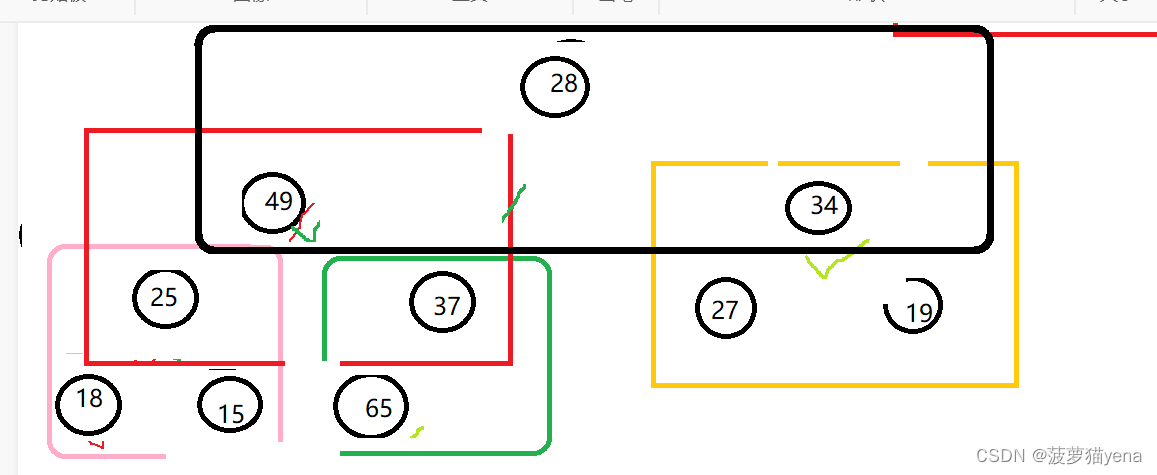
之后,在不动65的基础上再次把树调整为大根堆,从根元素开始向下调整
在这里文字描述.根元素28,小于左孩子结点值49,交换28与49,之后以28为父亲结点的子树,28小于右孩子节点值37,交换28与37.到这里,一个大根堆又建造好了.建好的大根堆如下图所示.

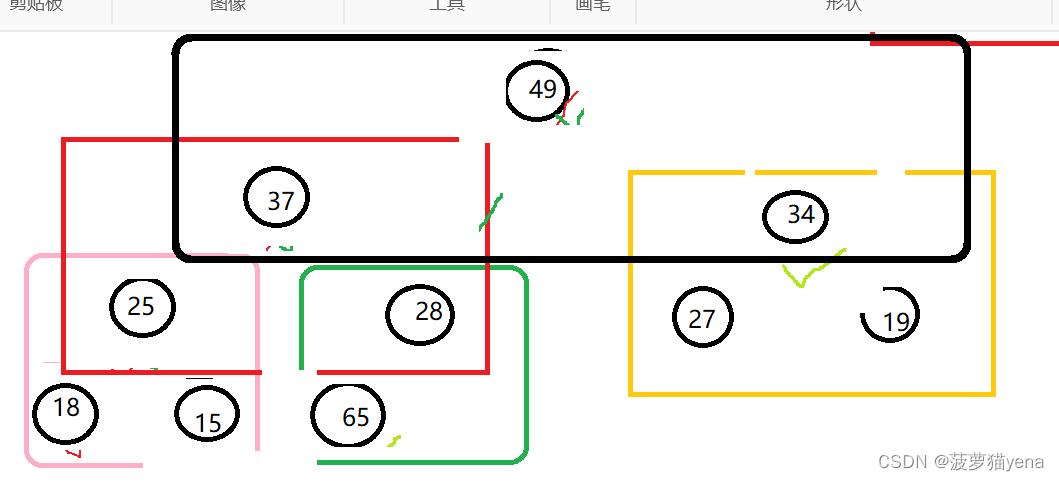
同样,49是第二大的元素,将49与倒数第二个元素15交换,这样,就把倒数第二大的元素换到倒数第二的位置了.
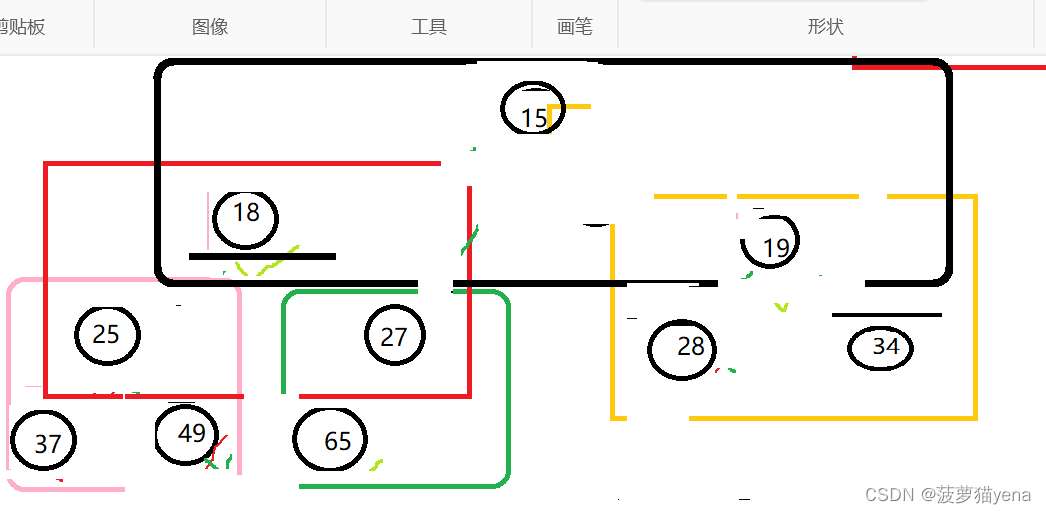
同样的方法,再次调整为大根堆,交换堆顶元素和末尾元素的值.这里大家自己操作试试.展示排好序的树

7.3 代码详解

第一步,建大根堆,从上图中我们看到,建大根堆是需要从最后一棵树的父亲结点开始调整.比较父亲结点与数值较大的孩子节点.一直到调整完第一棵树.
最后一棵树的父亲结点是啥捏.我们知道最后一个节点坐标是arr.length-1,那么它的父亲结点坐标就是==(arr.length-1-1)/2==.OK,循环的开始条件为(parent = (arr.length-1-1)/2),如下循环

		for(int parent = (array.length-1-1)/2; parent >= 0; parent--){
            shiftDown(array, parent, array.length);
        }

第二步,调整每一棵树,就是找到左右孩子的较大值,与父亲结点比较,比父亲结点大,则交换.再往后观察,看调整完之后有没有影响后面的树.

			if(child+1 < len && array[child+1] > array[child]){
                child++;
            }
            if(array[parent] < array[child]){
                swap(array, parent, child);
            }
  

如下图,调整完第一棵树后,发现父亲结点为15的树不满足条件了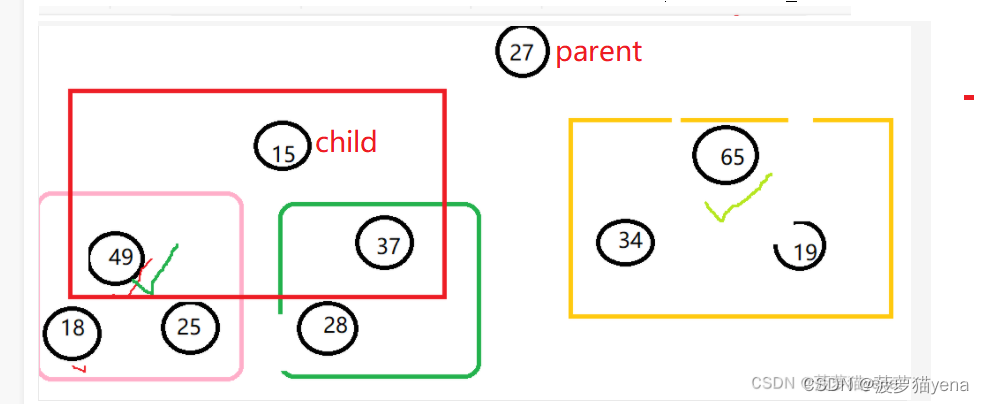
所以,我们要注意,调整完一棵树后,我们要检查一下后面的树还是否满足条件,不满足的话,还得继续往后调整一下.这里,令parent = child,child = 2 * parent +1, 再次进入循环,直到检查完最后一棵树,也就是child = arr.length时,跳出循环.

综上,调整树的代码如下

	private static void shiftDown(int[] array, int parent, int len){
        //从parent位置开始向下调整，调整一次后，parent = child, child = 2*parent + 1,child>len时跳出循环
        int child = 2*parent + 1;
        while(child < len){
            if(child+1 < len && array[child+1] > array[child]){
                child++;
            }
            if(array[parent] < array[child]){
                swap(array, parent, child);
            }
            parent = child;
            child = 2*parent + 1;
        }
    }

建完大根堆之后,就一次将堆顶元素与最后一个元素交换,换完之后,再把树调整为大根堆,再交换.需要注意的一点是,换好的元素就不能参与下一次循环了,所以,end要自减1.

		int end = array.length-1;
        while(end >= 0){
            swap(array,0,end);
            shiftDown(array,0,end);
            end--;
        }

综上,完整代码如下

public static void heapSort(int[] array){
        create(array);
        int end = array.length-1;
        while(end >= 0){
            swap(array,0,end);
            shiftDown(array,0,end);
            end--;
        }
    }

    private static void create(int[] array){
        for(int parent = (array.length-1-1)/2; parent >= 0; parent--){
            shiftDown(array, parent, array.length);
        }
    }
    private static void shiftDown(int[] array, int parent, int len){
        //从parent位置开始向下调整，调整一次后，parent = child, child = 2*parent + 1,child>len时跳出循环
        int child = 2*parent + 1;
        while(child < len){
            if(child+1 < len && array[child+1] > array[child]){
                child++;
            }
            if(array[parent] < array[child]){
                swap(array, parent, child);
            }
            parent = child;
            child = 2*parent + 1;
        }
    }

    public static void swap(int[] array, int parent, int child){
        int tmp = array[parent];
        array[parent] = array[child];
        array[child] = tmp;
    }

7.4 时间复杂度,空间复杂度分析.

时间复杂度: O(n x log n)
空间复杂度: O(1)

---

总结

总算总算是完成了,我们收藏起来多复习吧,不复习的话,没几天就忘没了,大家加油鸭!!