【负荷预测、电价预测】基于神经网络的负荷预测和价格预测（Matlab代码实现）

👨‍🎓个人主页：研学社的博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

1 概述

2 基于神经网络的负荷预测（Matlab实现）

2.1 部分代码

2.2 结果

2.3 回归树模型的进一步改进

3 基于神经网络的价格预测（Matlab代码实现）

4 Matlab代码及数据

1 概述

本文用MATLAB建立一个短期电力负荷（或价格）预测系统。两个非线性回归模型（神经网络和袋式回归树）被校准，以预测给定温度预测、假日信息和历史负荷的每小时前日负荷。这些模型在数据上进行训练，并在2008年的样本外数据上进行测试。这些模型被证明能够产生高度准确的日前预测，平均误差在1-2%左右。能够通过MATLAB部署的DLL调用训练好的负荷预测模型。

准确的负荷预测对于公用事业的短期运营和长期规划至关重要。负荷预测会影响许多决策，包括在给定时期内承诺哪些发电机，并广泛影响批发电力市场价格。负荷和价格预测算法通常在简化形式的电价混合模型中也很突出，这是用于模拟市场和模拟能源衍生品的一些最准确的模型。市场参与者在许多交易和风险管理应用程序中也广泛使用电价预测。负荷预测会影响许多决策，包括在给定时期内承诺哪些发电机，并广泛影响批发电力市场价格。负荷预测算法通常在电价混合模型中也很突出，这是电力市场建模最准确的一类方法。市场参与者在许多交易和风险管理应用程序中广泛使用电价预测。传统上，公用事业和营销人员使用商业软件包来执行负荷预测。这些方法的主要缺点是它们是一个黑匣子，不提供如何计算负载预测的透明度。它们通常也只提供实用程序所需功能的 80-90%。在许多情况下，不可能通过现成的产品满足所有要求，例如考虑到区域负载、不同的天气模式等。

2 基于神经网络的负荷预测（Matlab实现）

2.1 部分代码

%% 利用神经网络进行电力负荷预测
% 这个例子展示了用MATLAB建立和验证一个短期的
% 本例演示了用MATLAB建立和验证短期电力负荷预测模型。这些模型考虑到了

load Data\DBLoadData.mat
addpath ..\Util

%% 从Excel电子表格中导入假期列表

[num, text] = xlsread('..\Data\Holidays.xls'); 
holidays = text(2:end,1);


%% 生成预测矩阵
% 函数*genPredictors*生成了作为模型输入的预测变量。
% 的输入。对于短期预测，这些变量包括
% * 干球温度
% * 露点
% *一天中的小时
% * 一周中的一天
% *表明是否为假日/周末的标志
% * 前一天的平均负荷
% * 前一天同一小时的负荷
% * 前一周同一小时和同一天的负荷
% 如果目标是中期或长期的负荷预测，只需输入
% 如果目标是中期或长期的负荷预测，只有一天中的小时，一周中的一天，一年中的时间和节假日可以被使用
% 确定性地使用。天气/负荷信息将需要被指定为
% 指定为一个平均数或一个分布
%% 选择预测范围
term = 'short';

[X, dates, labels] = genPredictors(data, term, holidays);

%% 讲数据集分为训练和测试集
% 该数据集被分为两组，一个是包括2004年至2007年数据的_训练_组，
% 另一个是包括2008年数据的_测试_组。
% 训练集包括2004至2007年的数据，测试集包括2008年的数据。
% 训练集用于建立模型（估计其参数）。测试集仅用于预测，以测试模型在样本外数据上的表现。
%++++++ 建立训练集++++++++++
trainInd = data.NumDate < datenum('2008-01-01');
trainX = X(trainInd,:);
trainY = data.SYSLoad(trainInd);

%++++++创建测试集并保存以备不时之需++++++
testInd = data.NumDate >= datenum('2008-01-01');
testX = X(testInd,:);
testY = data.SYSLoad(testInd);
testDates = dates(testInd);

save Data\testSet testDates testX testY
clear X data trainInd testInd term holidays dates ans num text

%% 构建负荷预测模型
% 接下来的几个单元建立了一个神经网络回归模型，
% 用于给定训练数据的日前负荷预测。
% 然后，该模型被用于测试数据以验证其准确性。
%% 初始化和训练网络
% 初始化一个包含 20 个神经元的两层默认网络。使用“平均
% 绝对误差”（MAE）性能指标。然后，用
% 默认的 Levenburg-Marquardt 算法。为了提高效率，预先训练
% 除非特别强制执行重新训练，否则网络会被加载。
reTrain = false;
if reTrain || ~exist('Models\NNModel.mat', 'file')
    net = newfit(trainX', trainY', 20);
    net.performFcn = 'mae';
    net = train(net, trainX', trainY');
    save Models\NNModel.mat net
else
    load Models\NNModel.mat
end
    
%% 采用神经网络模型进行预测
% 一旦建立了模型，对独立的测试集进行预测. 

load Data\testSet
forecastLoad = sim(net, testX')';

%% 比较预测负荷和实际负荷
% 创建一个图表来比较实际负荷和预测负荷以及
% 并计算出预测误差。除了可视化之外，还可以使用平均绝对值等指标来量化
% 预测器的性能，如平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和每日峰值误差（MAPE）等指标。
% 误差（MAE），平均绝对误差（MAPE）和每日峰值预测
% 误差。
err = testY-forecastLoad;
fitPlot(testDates, [testY forecastLoad], err);

errpct = abs(err)./testY*100;

fL = reshape(forecastLoad, 24, length(forecastLoad)/24)';
tY = reshape(testY, 24, length(testY)/24)';
peakerrpct = abs(max(tY,[],2) - max(fL,[],2))./max(tY,[],2) * 100;

MAE = mean(abs(err));
MAPE = mean(errpct(~isinf(errpct)));

fprintf('平均绝对百分比误差 (MAPE): %0.2f%% \n平均绝对误差 (MAE): %0.2f MWh\n每日峰值 MAPE: %0.2f%%\n',...
    MAPE, MAE, mean(peakerrpct))


%% 检查误差的分布情况
% 除了报告标量误差指标（如MAE和MAPE）外，误差分布图和绝对误差也有助于建立
% 误差和绝对误差的分布图可以帮助建立
% 围绕预测者的表现建立直觉
%% 可视化图像
figure;
subplot(3,1,1); hist(err,100); title('误差分布');
subplot(3,1,2); hist(abs(err),100); title('绝对误差分布');
line([MAE MAE], ylim); legend('误差', 'MAE');
subplot(3,1,3); hist(errpct,100); title('绝对百分比误差分布');
line([MAPE MAPE], ylim); legend('误差', 'MAPE');

%% 误差的集体分析
% 为了进一步了解预报器的性能，我们可以
% 为了进一步了解预报员的表现，我们可以按一天中的每一小时、
% 一周中的每一天和一年中的每一个月来直观地显示预报误差百分比。
% 年的月份
[yr, mo, da, hr] = datevec(testDates);

%% 按小时计算
clf;
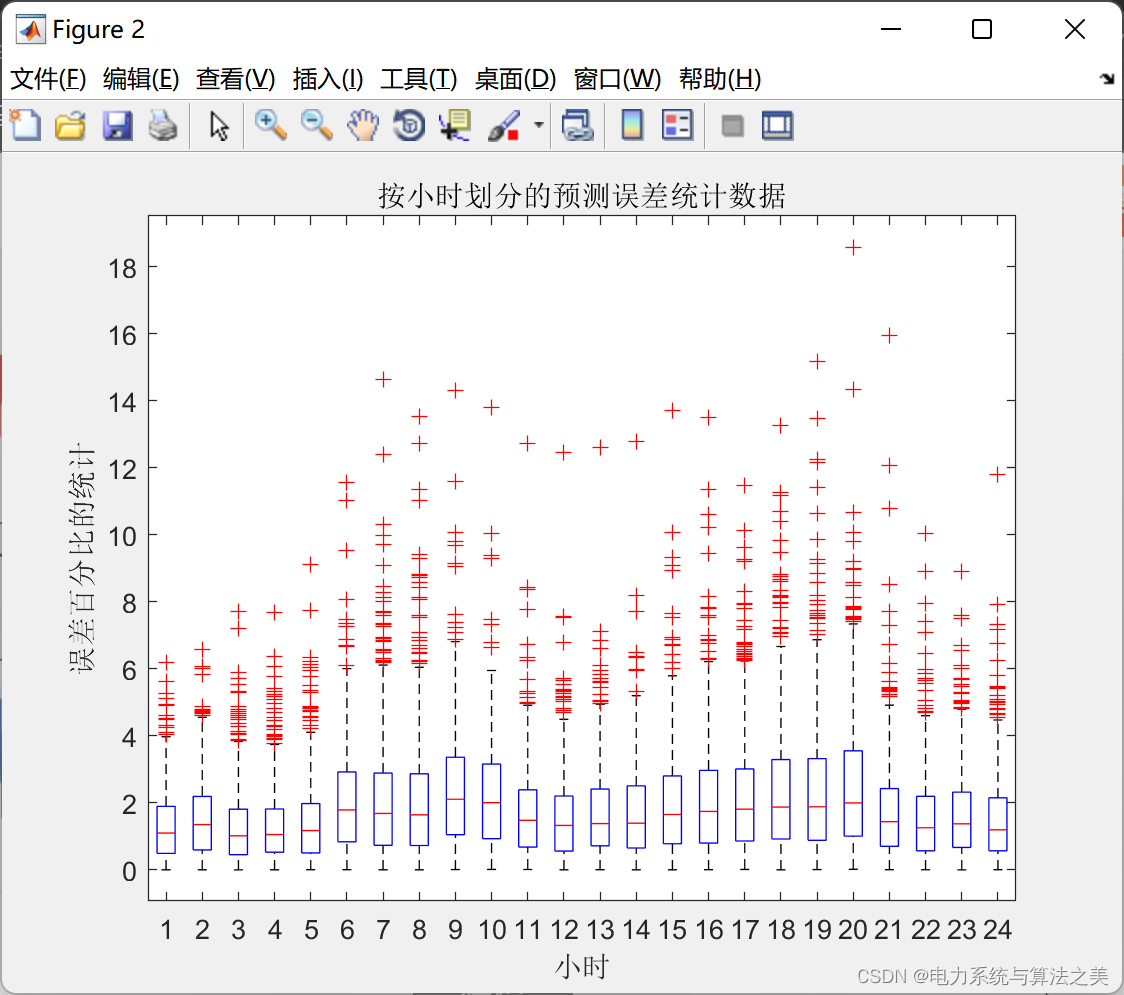
boxplot(errpct, hr+1);
xlabel('小时'); ylabel('误差百分比的统计');
title('按小时划分的预测误差统计数据');

% 按工作日
figure
boxplot(errpct, weekday(floor(testDates)), 'labels', {'Sun','Mon','Tue','Wed','Thu','Fri','Sat'});
ylabel('误差百分比统计');
title('按工作日划分的预测误差统计明细表');

% 按月份
figure
boxplot(errpct, datestr(testDates,'mmm'));
ylabel('误差百分比统计');
title('按月份划分的预测误差统计细目表');


%% 制作每周图表
%在测试集上每周建立预测负荷与实际负荷的对比。
generateCharts = true;
if generateCharts
    step = 168*2;
    for i = 0:step:length(testDates)-step
        clf;
        fitPlot(testDates(i+1:i+step), [testY(i+1:i+step) forecastLoad(i+1:i+step)], err(i+1:i+step));
        title(sprintf('MAPE: %0.2f%%', mean(errpct(i+1:i+step))));
        snapnow
        
    end
end

%% 利用神经网络进行电力负荷预测
% 这个例子展示了用MATLAB建立和验证一个短期的
% 本例演示了用MATLAB建立和验证短期电力负荷预测模型。这些模型考虑到了
% 考虑到多种信息来源，包括温度和
% 假期等多种信息，以构建一个日前负荷预测器。这个脚本使用
% 神经网络。

%% 导入天气和负荷数据
% 所使用的数据集是一个地区2004 - 2008年的历史小时负荷和温度观测表。
% 天气信息包括干球温度和露点。
load Data\DBLoadData.mat
addpath ..\Util

%% 从Excel电子表格中导入假期列表

[num, text] = xlsread('..\Data\Holidays.xls');
holidays = text(2:end,1);

%% 生成预测矩阵
% 函数*genPredictors*生成了作为模型输入的预测变量。
% 的输入。对于短期预测，这些变量包括
% * 干球温度
% * 露点
% *一天中的小时
% * 一周中的一天
% *表明是否为假日/周末的标志
% * 前一天的平均负荷
% * 前一天同一小时的负荷
% * 前一周同一小时和同一天的负荷
% 如果目标是中期或长期的负荷预测，只需输入
% 如果目标是中期或长期的负荷预测，只有一天中的小时，一周中的一天，一年中的时间和节假日可以被使用
% 确定性地使用。天气/负荷信息将需要被指定为
% 指定为一个平均数或一个分布
%% 选择预测范围
term = 'short';

[X, dates, labels] = genPredictors(data, term, holidays);

%% 讲数据集分为训练和测试集
% 该数据集被分为两组，一个是包括2004年至2007年数据的_训练_组，
% 另一个是包括2008年数据的_测试_组。
% 训练集包括2004至2007年的数据，测试集包括2008年的数据。
% 训练集用于建立模型（估计其参数）。测试集仅用于预测，以测试模型在样本外数据上的表现。
%++++++ 建立训练集++++++++++
trainInd = data.NumDate < datenum('2008-01-01');
trainX = X(trainInd,:);
trainY = data.SYSLoad(trainInd);

%++++++创建测试集并保存以备不时之需++++++
testInd = data.NumDate >= datenum('2008-01-01');
testX = X(testInd,:);
testY = data.SYSLoad(testInd);
testDates = dates(testInd);

save Data\testSet testDates testX testY
clear X data trainInd testInd term holidays dates ans num text

%% 构建负荷预测模型
% 接下来的几个单元建立了一个神经网络回归模型，
% 用于给定训练数据的日前负荷预测。
% 然后，该模型被用于测试数据以验证其准确性。
%% 初始化和训练网络
% 初始化一个包含 20 个神经元的两层默认网络。使用“平均
% 绝对误差”（MAE）性能指标。然后，用
% 默认的 Levenburg-Marquardt 算法。为了提高效率，预先训练
% 除非特别强制执行重新训练，否则网络会被加载。
reTrain = false;
if reTrain || ~exist('Models\NNModel.mat', 'file')
net = newfit(trainX', trainY', 20);
net.performFcn = 'mae';
net = train(net, trainX', trainY');
save Models\NNModel.mat net
else
load Models\NNModel.mat
end

%% 采用神经网络模型进行预测
% 一旦建立了模型，对独立的测试集进行预测.

load Data\testSet
forecastLoad = sim(net, testX')';

%% 比较预测负荷和实际负荷
% 创建一个图表来比较实际负荷和预测负荷以及
% 并计算出预测误差。除了可视化之外，还可以使用平均绝对值等指标来量化
% 预测器的性能，如平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和每日峰值误差（MAPE）等指标。
% 误差（MAE），平均绝对误差（MAPE）和每日峰值预测
% 误差。
err = testY-forecastLoad;
fitPlot(testDates, [testY forecastLoad], err);

errpct = abs(err)./testY*100;

fL = reshape(forecastLoad, 24, length(forecastLoad)/24)';
tY = reshape(testY, 24, length(testY)/24)';
peakerrpct = abs(max(tY,[],2) - max(fL,[],2))./max(tY,[],2) * 100;

MAE = mean(abs(err));
MAPE = mean(errpct(~isinf(errpct)));

fprintf('平均绝对百分比误差 (MAPE): %0.2f%% \n平均绝对误差 (MAE): %0.2f MWh\n每日峰值 MAPE: %0.2f%%\n',...
MAPE, MAE, mean(peakerrpct))

%% 检查误差的分布情况
% 除了报告标量误差指标（如MAE和MAPE）外，误差分布图和绝对误差也有助于建立
% 误差和绝对误差的分布图可以帮助建立
% 围绕预测者的表现建立直觉
%% 可视化图像
figure;
subplot(3,1,1); hist(err,100); title('误差分布');
subplot(3,1,2); hist(abs(err),100); title('绝对误差分布');
line([MAE MAE], ylim); legend('误差', 'MAE');
subplot(3,1,3); hist(errpct,100); title('绝对百分比误差分布');
line([MAPE MAPE], ylim); legend('误差', 'MAPE');

%% 误差的集体分析
% 为了进一步了解预报器的性能，我们可以
% 为了进一步了解预报员的表现，我们可以按一天中的每一小时、
% 一周中的每一天和一年中的每一个月来直观地显示预报误差百分比。
% 年的月份
[yr, mo, da, hr] = datevec(testDates);

%% 按小时计算
clf;
boxplot(errpct, hr+1);
xlabel('小时'); ylabel('误差百分比的统计');
title('按小时划分的预测误差统计数据');

% 按工作日
figure
boxplot(errpct, weekday(floor(testDates)), 'labels', {'Sun','Mon','Tue','Wed','Thu','Fri','Sat'});
ylabel('误差百分比统计');
title('按工作日划分的预测误差统计明细表');

% 按月份
figure
boxplot(errpct, datestr(testDates,'mmm'));
ylabel('误差百分比统计');
title('按月份划分的预测误差统计细目表');

%% 制作每周图表
%在测试集上每周建立预测负荷与实际负荷的对比。
generateCharts = true;
if generateCharts
step = 168*2;
for i = 0:step:length(testDates)-step
clf;
fitPlot(testDates(i+1:i+step), [testY(i+1:i+step) forecastLoad(i+1:i+step)], err(i+1:i+step));
title(sprintf('MAPE: %0.2f%%', mean(errpct(i+1:i+step))));
snapnow

end
end