代码随想录day42和day43 动态规划 模块01背包问题
“即使到不了远方,心中也要有远方的模样。”
文章目录
- 1. 01背包理论基础
- 1.1什么是背包问题
- 1.2二维dp数组01背包
- 1.3一维dp数组(滚动数组)01背包
- 2.leetcode 416.分割等和子集
- 2.1 详细思路及思考难点
- 2.2具体步骤及代码实现
- 3.leetcode 1049.最后一块石头的重量
- 3.1详细思路及思考难点
- 3.2具体步骤及代码实现
- 4.leetcode 494.目标和
- 4.1详细思路及思考难点
- 4.2具体步骤及代码实现
- 5.leetcode 474.一和零
- 5.1详细思路及思考难点
- 5.2具体步骤及代码实现
1. 01背包理论基础
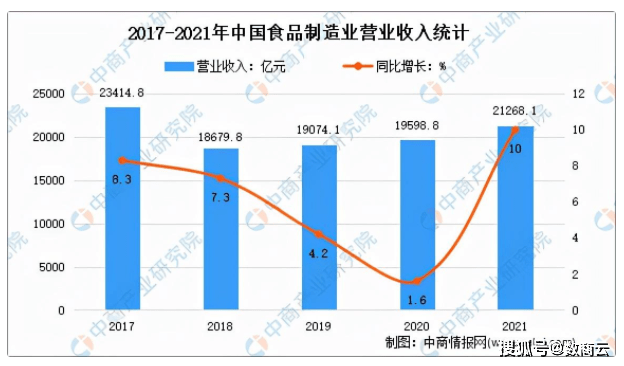
1.1什么是背包问题

背包问题大致可以分为以上几类,背包问题也就是选取物品放入重量为n的背包中,然后求背包的最大价值。
1.2二维dp数组01背包
01背包问题—有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。

例子:假设背包最大重量为4,然后有三个物品,看如何将物品放入背包中能获取最大价值。
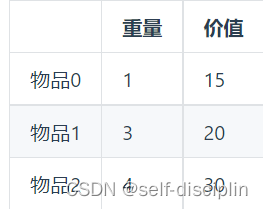
还是可以用动态规划的做题步骤来分析
1.确定dp数组以及下标的含义
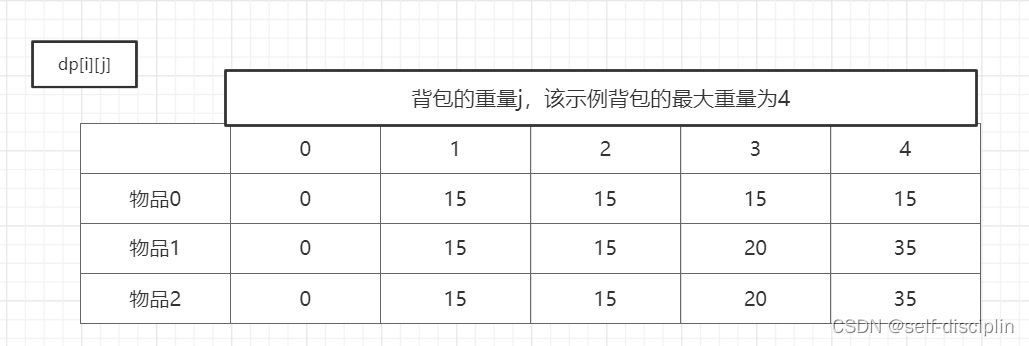
dp[i][j]对应的就是取索引[0,i]的物品,放入重量为j的背包中,得到价值dp[i][j]
2. 确定递推公式
可以先将每种情况列举出来,然后再推导公式
由此可以推导出递推公式为dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
每次遍历到dp[i][j]的时候都有两种取值情况dp[i-1][j]表示不放物品时的情况
dp[i-1][j-weight[i]]+value[i],weight[i]表示i的重量,value[i]表示i的价值。这就是表示添加新物品的情况
在上面两种情况中取最值
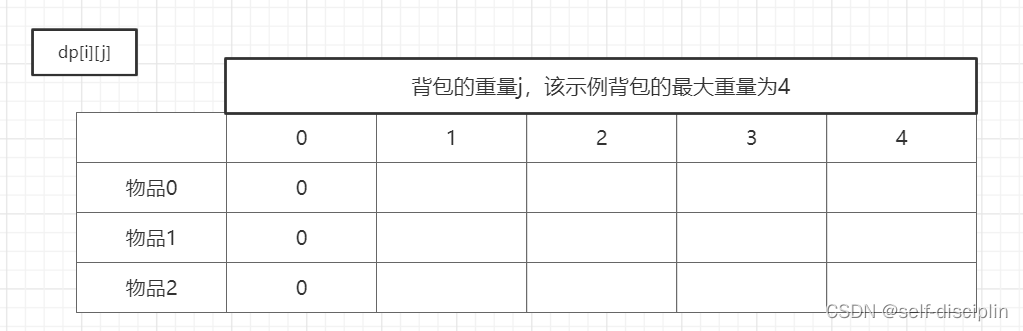
3. dp数组的初始化问题
当背包重量为0时,可以初始化dp[i][0]=0;
4.确定遍历顺序
这题的从前往后面遍历,可以先遍历背包再遍历物品也可以先便利物品再遍历背包,一般是先遍历物品
5. 举例推导dp公式
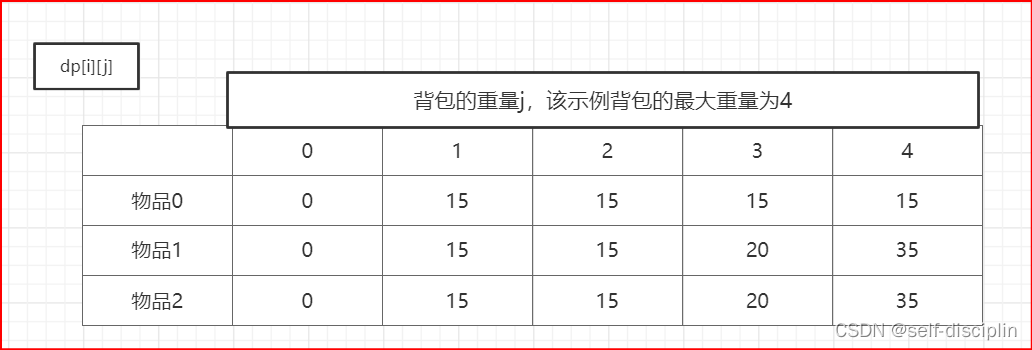
代码示例
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
testweightbagproblem(weight, value, bagsize);
}
public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
int wlen = weight.length, value0 = 0;
//定义dp数组:dp[i][j]表示背包容量为j时,前i个物品能获得的最大价值
int[][] dp = new int[wlen + 1][bagsize + 1];
//初始化:背包容量为0时,能获得的价值都为0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
}
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 1; i <= wlen; i++){
for (int j = 1; j <= bagsize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
//打印dp数组
for (int i = 0; i <= wlen; i++){
for (int j = 0; j <= bagsize; j++){
System.out.print(dp[i][j] + " ");
}
System.out.print("\n");
}
}
1.3一维dp数组(滚动数组)01背包
上面用二维数组来解决01背包问题,其实也可以用一维数组(也叫做滚动数组)来解决01背包问题。其核心也就是将二维数组压缩成一维数组。
假设背包最大重量为4,然后有三个物品,看如何将物品放入背包中能获取最大价值。

那还是按照动态规划的做题步骤来分析
1.确定dp数组以及下标的含义
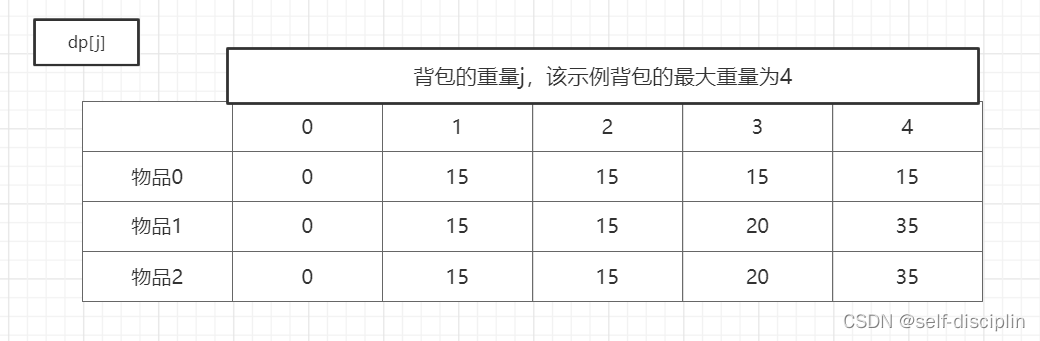
dp[j]对应的就是背包重量为j的时候对应的最大价值dp[j]
2. 确定递推公式
可以先将每种情况列举出来,然后再推导公式
dp[j]是由dp[j-weight[i]]决定的,递推公式可以如下
dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i])
3. dp数组的初始化问题
当背包重量为0时,可以初始化dp[0]=0;
4.确定遍历顺序
这题先遍历物品的时候可以从前面往后面遍历,然后再背包的时候得从后面往前面进行倒序遍历。如果是顺序遍历的话物品就会重复添加,因为每个物品只能用一次,以免影响其他结果
5. 举例推导dp公式
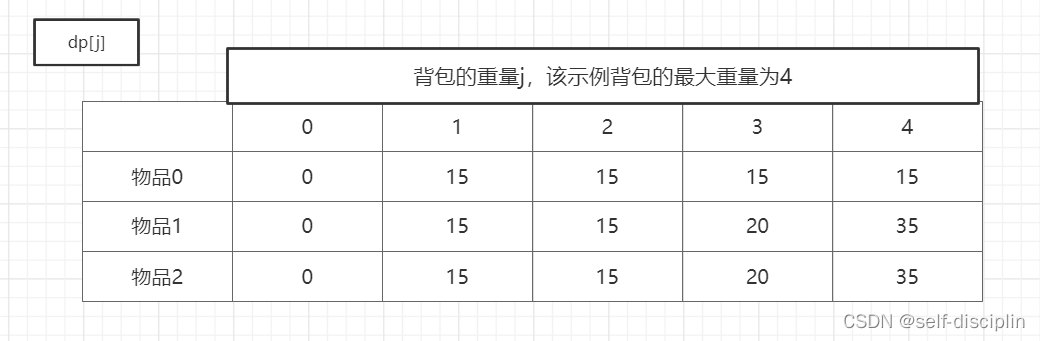
代码示例
public static void main(String[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWight = 4;
testWeightBagProblem(weight, value, bagWight);
}
public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
int wLen = weight.length;
//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值
int[] dp = new int[bagWeight + 1];
//遍历顺序:先遍历物品,再遍历背包容量
for (int i = 0; i < wLen; i++){
for (int j = bagWeight; j >= weight[i]; j--){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
//打印dp数组
for (int j = 0; j <= bagWeight; j++){
System.out.print(dp[j] + " ");
}
}
2.leetcode 416.分割等和子集
力扣题目链接
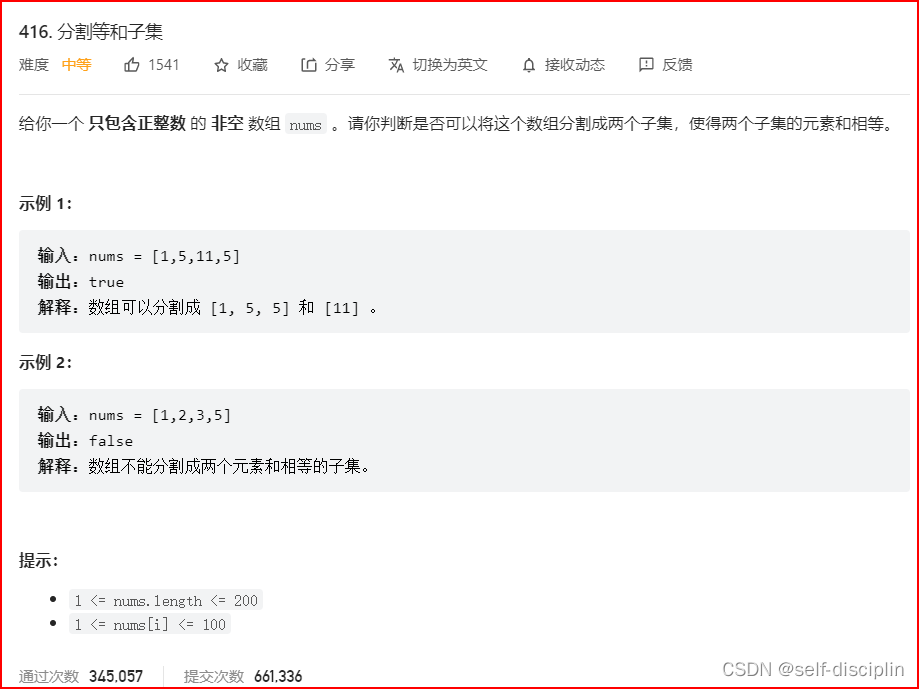
2.1 详细思路及思考难点
这题可以将其划分为01背包问题,给定一个数组,判断是否能将数组分成两个子集和相同的两个数组。要将数组分成两个相等的子集的话,数组中的和sum也就是必须是偶数(这是第一个判断条件),然后令target=sum/2;这就是子集的和,把target想象成一个背包的最大重量,现在就是让背包里面的物品的重量刚好能达到背包的最大重量,如果能达到就返回true,反之,return false。
2.2具体步骤及代码实现
按照动态规划的做题步骤来分析
1.确定dp数组以及下标的含义
dp[j]对应的就是背包重量为j的时候对应的最大价值dp[j]
2. 确定递推公式
dp[j]是由dp[j-weight[i]]决定的,递推公式可以如下
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]),这里nums[i]既可以表示重量也可以表示价值
3. dp数组的初始化问题
当背包重量为0时,可以初始化dp[0]=0;
4.确定遍历顺序
这题先遍历物品的时候可以从前面往后面遍历,然后再背包的时候得从后面往前面进行倒序遍历。因为每个物品只能用一次,以免影响其他结果
5. 举例推导dp公式
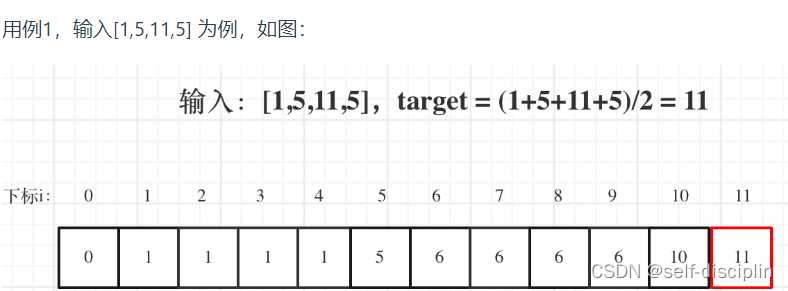
代码实现
class Solution {
public boolean canPartition(int[] nums) {
if(nums==null || nums.length==0)return false;
int sum=0;
for(int a:nums){
sum+=a;
}
if(sum%2!=0)return false;
int targrt=sum/2;
int[] dp=new int[targrt+1];
//dp[0]=0;
for(int i=0;i<nums.length;i++){
for(int j=targrt;j>=nums[i];j--){
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
return dp[targrt]==targrt;
}
}
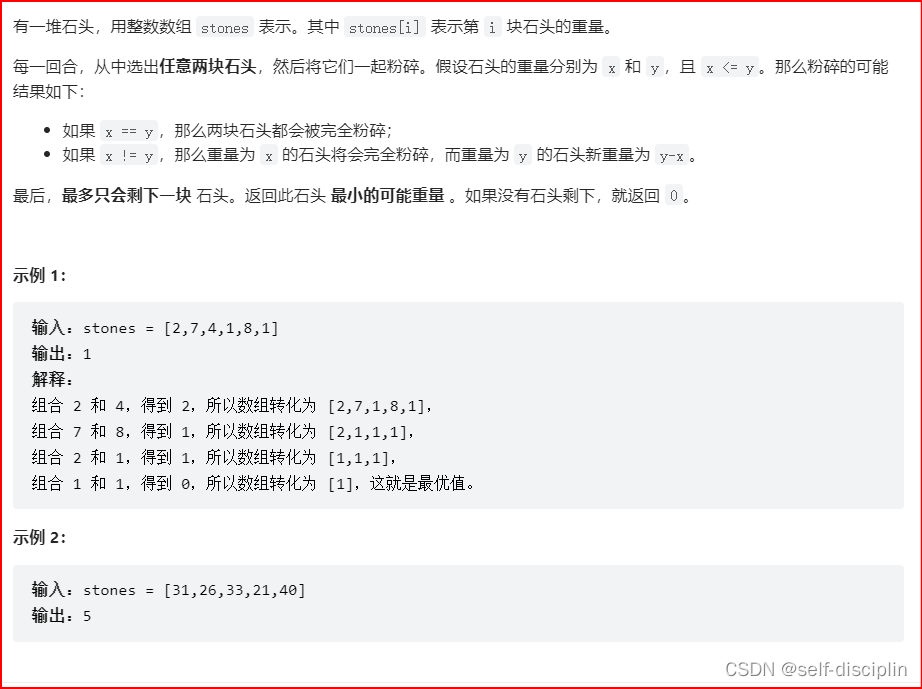
3.leetcode 1049.最后一块石头的重量
力扣题目链接
3.1详细思路及思考难点
这题思路跟416.分割子集问题基本一致,可以将所有石头分成两份和相同的子集和,target=sum/2,然后将石头存入dp[target]中所能满足的最大价值,最终返回的结果是(sum-dp[target])-dp[target],(sum-dp[target])表示没有装入背包的所有的集合,然后减去装入背包的,就是碰撞之后剩下的量。
3.2具体步骤及代码实现
按照动态规划的做题步骤来分析
1.确定dp数组以及下标的含义
dp[j]对应的就是背包重量为j的时候对应的最大石头量dp[j]
2. 确定递推公式
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
3. dp数组的初始化问题
当背包重量为0时,可以初始化dp[0]=0;
4.确定遍历顺序
这题先遍历物品的时候可以从前面往后面遍历,然后再背包的时候得从后面往前面进行倒序遍历。因为每个物品只能用一次,以免影响其他结果
5. 举例推导dp公式
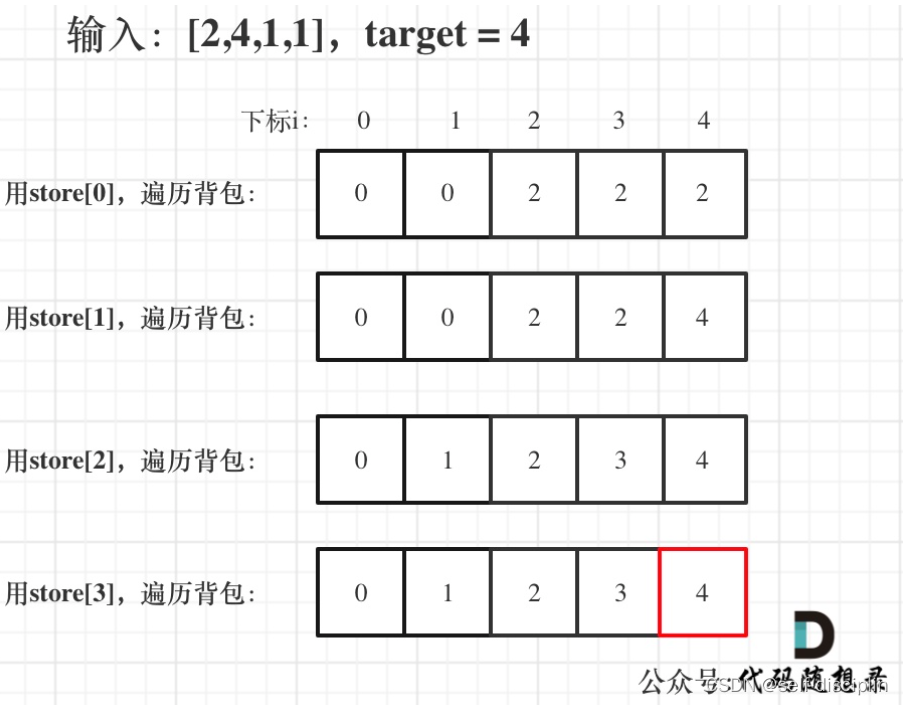
代码实现
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum=0;
for(int a:stones){
sum+=a;
}
int target=sum>>1;
int[] dp=new int[target+1];
dp[0]=0;
for(int i=0;i<stones.length;i++){
for(int j=target;j>=stones[i];j--){
dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return sum-dp[target]-dp[target];
}
}
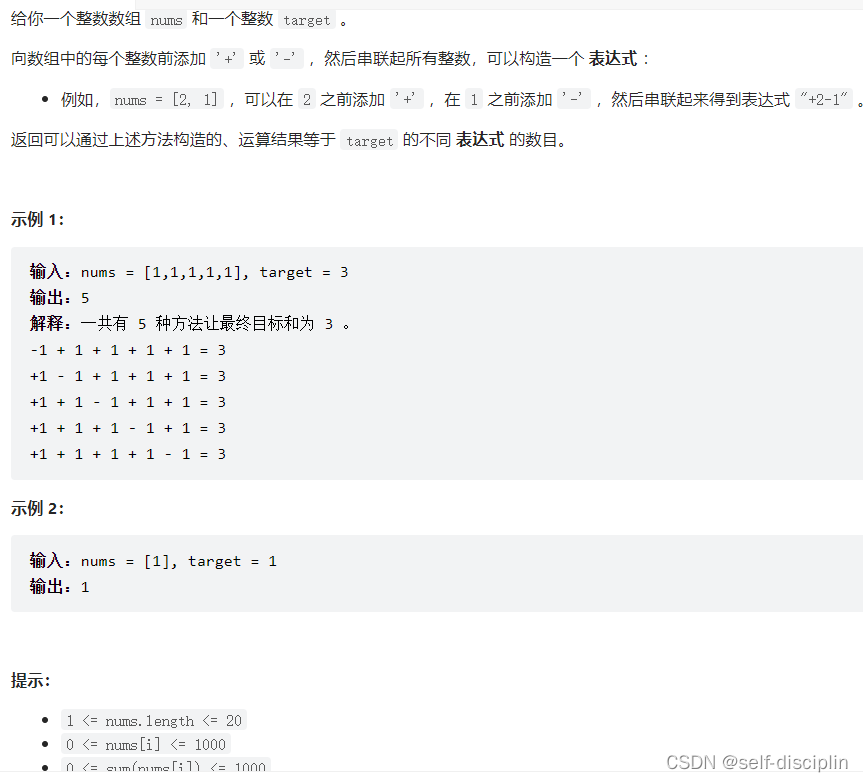
4.leetcode 494.目标和
力扣题目链接
4.1详细思路及思考难点
将nums中的数值添加正负号之后,设正数和为x,那么负数的和就是sum-x(sum是nums数组中所有元素的和)。x-(sum-x)=target ==>x=(sum+target)/2。然后将x转换成填满大小为x的背包,需要dp[j]种方法。
4.2具体步骤及代码实现
按照动态规划的做题步骤来分析
1.确定dp数组以及下标的含义
dp[j]对应的就是背包重量为j的时候对应的最大价值dp[j]
2. 确定递推公式
根据下面得出递推公式为dp[j]+=dp[j-nums[i]]
- 已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 dp[5]。
- 已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 dp[5]。
- 已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 dp[5]
- 已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 dp[5]
- 已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 dp[5]
3. dp数组的初始化问题
当背包重量为0时,可以初始化dp[0]=0;
4.确定遍历顺序
这题先遍历物品的时候可以从前面往后面遍历,然后再背包的时候得从后面往前面进行倒序遍历。因为每个物品只能用一次,以免影响其他结果
代码实现
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum=0;
for(int a:nums){
sum+=a;
}
int zs=(sum+target)/2;
if((target+sum)%2!=0) return 0;
if(zs<0)zs=-zs;
int[] dp=new int[zs+1];
if(target>sum)return 0;
dp[0]=1;
for(int i=0;i<nums.length;i++){
for(int j=zs;j>=nums[i];j--){
dp[j]+=dp[j-nums[i]];
}
}
return dp[zs];
}
}
5.leetcode 474.一和零
力扣题目链接

5.1详细思路及思考难点
这题用二维dp数组来做,把每个字符串当作单独的物品,总共的0和1的个数当作背包的容量。
5.2具体步骤及代码实现
按照动态规划的做题步骤来分析
1.确定dp数组以及下标的含义
dp[i][j]表示当有i个0和j个1时的最大子集的大小
2. 确定递推公式
根据下面得出递推公式为dp[i][j]=Math.max(dp[i][j],dp[i-zero][j-one]+1)
3. dp数组的初始化问题
初始为0就可以
4.确定遍历顺序
遍历字符串的时候顺序遍历,遍历0和1的时候倒叙
5.推导dp数组
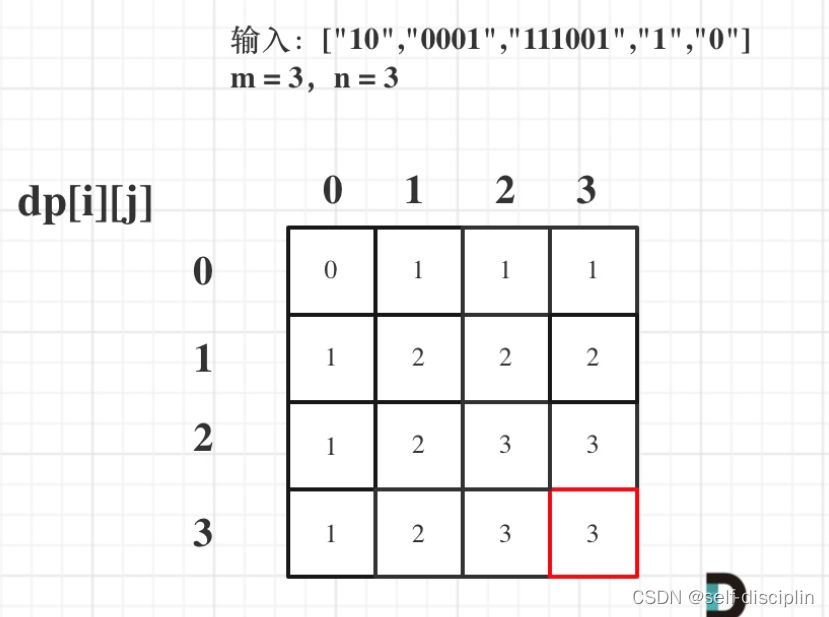
代码实现
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp=new int[m+1][n+1];
int zero,one;
for(String s : strs){
zero=0;
one=0;
for(char c:s.toCharArray()){
if(c=='0'){
zero++;
}else if(c== '1'){
one++;
}
}
for(int i=m;i>=zero;i--){
for(int j=n;j>=one;j--){
dp[i][j]=Math.max(dp[i][j],dp[i-zero][j-one]+1);
}
}
}
return dp[m][n];
}
}